Tooth Flank Fracture, progetto di un nuovo ingranaggio di prova e primi risultati

Progetto di un nuovo ingranaggio di prova appositamente concepito per effettuare prove di Tooth Flank Fracture in modo efficiente su banchi standard tipo FZG. Applicazione del metodo di calcolo secondo ISO/TS 6336-4. Discussione dei principali fattori di influenza e analisi dei primi di risultati di prova.

La frattura del fianco del dente, TFF (da Tooth Flank Fracture) è una modalità di cedimento per fatica degli ingranaggi. Di recente si sta verificando con frequenza crescente. Una probabile causa di questa maggiore incidenza è l’aumento della densità di potenza nelle trasmissioni a ingranaggi ma anche il fatto che gli altri cedimenti classici, come il pitting e la frattura al piede, sono stati largamente investigati e possono essere evitati in modo affidabile utilizzando i metodi di calcolo a norma secondo ISO [1] e AGMA [2].

La TFF differisce significativamente dal pitting e dalla frattura a piede dente perché la nucleazione della cricca avviene a una maggiore profondità. La cricca che avanza non è visibile dall’esterno fino alla rottura finale, che usualmente determina l’avaria del riduttore. Per questo motivo è necessario sviluppare un metodo di calcolo per la TFF, per poter prevenire in modo affidabile fin dalla fase di progetto il danneggiamento in esercizio.

La ISO/TS 6336-4 [3] per il calcolo della capacità di carico rispetto alla TFF è un approccio di calcolo fondato e validato sulla base di risultati sperimentali su ingranaggio di prova con interasse a = 200 mm e di svariate indagini su ingranaggi utilizzati nell’industria. A causa della novità di questo cedimento, ci sono relativamente poche indagini sperimentali su banchi prova, le quali consentirebbero un’estensiva validazione e miglioramento del metodo di calcolo a TFF.

Ad oggi sono disponibili solo ingranaggi di prova con interasse di 200 mm. La sperimentazione sistematica sulle altre modalità di cedimento, quali il pitting, il micropitting o lo scuffing, è usualmente condotta su ingranaggi di modulo 3-5 con un interasse a = 91,5 mm. Ingranaggi più piccoli consentono una sperimentazione più economica. Infatti, la costruzione di ingranaggi più grossi è più costosa, la manipolazione degli ingranaggi è più complessa e in genere si dispone di meno banchi con interassi elevati. E’ pertanto di assoluta necessità trovare ingranaggi più piccoli con i quali sia possibile investigare in modo efficace la TFF così da estendere e validare il metodo di calcolo.

L’approccio pratico della ISO/TS 6336-4viene qui utilizzato per progettare un ingranaggio di prova più piccolo, con interasse di 91,5 mm. Sono anche presentati e discussi I risultati di prove su un banco prova a ricircolo, insieme a ulteriori indagini riguardanti la microstruttura, la durezza e gli sforzi residui.

Tooth Flank Fracture

Caratterizzazione della Tooth Flank Fracture

La Tooth Flank Fracture (TFF) è un cedimento a fatica degli ingranaggi con la nucleazione di una cricca, che usualmente avviene dopo svariati milioni di cicli di carico, la quale conduce alla rottura del dente e alla conseguente avaria dell’ingranaggio. La TFF può avvenire negli ingranaggi cilindrici a denti dritti ed elicoidali [4] così come negli ingranaggi conici [5]. Questo danneggiamento è divenuto recentemente più frequente, soprattutto negli ingranaggi più grandi delle trasmissioni industriali [6-8].

La cricca primaria usualmente nuclea sotto la superficie del fianco caricato a una profondità elevata, indicativamente dell’ordine di quella di transizione alla durezza a cuore. Nel punto si rinvengono inclusioni parzialmente non metalliche. Dopo la nucleazione, la cricca propaga sotto la superficie, più lentamente verso la superficie del fianco caricato e più velocemente nel materiale a cuore di minor resistenza, verso il fianco opposto (figura 1, sinistra). La propagazione usualmente forma un fisheye.

In caso di carico variabile, è frequente vedere linee di spiaggia (beachmark) nel fisheye sulla superficie di frattura che mostrano la dipendenza della propagazione dal carico (figura 1, destra). Tipicamente la cricca non è visibile dall’esterno fino a quando il dente non cede del tutto per la rottura finale. La traiettoria della propagazione usualmente forma un angolo di ~45° dalla zona del punto primitivo del fianco caricato verso la zona del raccordo al piede del fianco opposto.

La cricca primaria può essere accompagnata da cricche secondarie e terziarie, che partono dalla superficie del fianco caricato. Per gli ingranaggi elicoidali, frequentemente si osserva che la rottura non interessa l’intera larghezza di dentatura. Per le dentature caricate su entrambi I fianchi, come quelle delle ruote oziose, si osserva una frattura di caratteristiche diverse, denominata tooth interior fatigue fracture (TIFF) [9-12].

Meccanismo di frattura e fattori di influenza

La nucleazione della TFF è dovuta alla fatica nel materiale ad elevata profondità, causata dagli sforzi dovuti al carico sugli ingranaggi. Gli sforzi di contatto sono considerati come sforzi primari e quelli derivanti dalla deformazione del dente come secondari.

Gli sforzi di contatto possono essere descritti mediante la teoria Hertziana, secondo la quale gli sforzi normali sono massimi in superficie e quelli di taglio hanno un massimo di 0,3 volte la pressione Hertziana di contatto (p_H) a una profondità di circa 0,8 volte la semiampiezza di contatto Hertziana (b_H).

Il raggio di curvatura relativa ρ_rel dell’ingranaggio è determinante per il valore assoluto della profondità del massimo sforzo di taglio così come della pressione di contatto Hertziana pH. Gli sforzi secondari sono ritardati nel tempo e usualmente sono significativamente minori. Gli sforzi di flessione sono massimi sulla superficie del fianco e quelli associati alla corrispondente forza di taglio sono massimi sull’asse del dente (figura 2 destra).

Gli sforzi secondari contribuiscono alla nucleazione e soprattutto alla propagazione della cricca. La nucleazione avviene dove gli sforzi di contatto sono già ridotti ma dove anche la resistenza del materiale è diminuita considerevolmente. Pertanto, il punto di nucleazione si trova usualmente nella zona sotto la superficie in corrispondenza della transizione tra lo strato cementato e il cuore. La resistenza locale del dente viene usualmente assunta proporzionale alla durezza. La durezza locale dipende sia dal materiale base sia dal trattamento termico e dai suoi parametri.

In aggiunta, vi sono fattori di influenza quali le proprietà della microstruttura locale così come il grado di pulizia del materiale. In corrispondenza delle inclusioni non metalliche, gli sforzi possono essere localmente più alti. Tipi diversi di inclusioni non metalliche causano differenti maggiori sforzi che possono nucleare la frattura [13]. La nucleazione è generalmente nell’area di transizione alla durezza a cuore, anche se le inclusioni di dimensioni più elevate possono spostare significativamente la profondità di nucleazione a causa di picchi locali di sforzo [14].

Gli sforzi residui sono un altro fattore di influenza rilevante. In superficie, gli elevati sforzi residui prevengono la nucleazione, mentre invece a profondità maggiori, i piccoli sforzi residui di compressione, o quelli di trazione, non sono in grado di prevenire la nucleazione e la propagazione, o possono addirittura favorirla (figura 2, sinistra).

Si assume che le influenze della rugosità del fianco, della lubrificazione e del lubrificante non abbiano effetto sulla frattura. Questi fattori hanno un impatto significativo sulle condizioni di lubrificazione elastoidrodinamica (EHL) e sugli sforzi sulla superficie e nelle immediate vicinanze ma, alle profondità più elevate, possono essere trascurati e a cinque volte la semiampiezza herziana b_H non hanno effetto.

Studi e prove sperimentali del calcolo a TFF di ingranaggi cementati

Bauer [6-8] ha pubblicato le sue osservazioni della modalità di cedimento nelle trasmissioni industriali e ha investigato la nuova modalità. Ha descritto le caratteristiche della TFF e ha indagato i suoi meccanismi. Tobie [15] ha osservato la modalità di cedimento in ingranaggi di prova con modulo 3 mm e interasse di 200 mm.

Si trattava di ingranaggi in acciaio da cementazione 16MnCr5 con profondità di cementazione (CHD) approssimativamente di 0,5 e 1,3 mm. La TFF usualmente si verificava in entrambe le varianti. La nucleazione della cricca veniva individuata a una profondità di 1,5-2 mm sotto il fianco caricato grosso modo a metà altezza del dente. Bruckmeier [16] ha eseguito ulteriori prove al banco su ingranaggi con la stessa geometria con una CHD di 0.55 mm e ha condotto indagini teoriche con l’approccio sviluppato da Oster [17].

Questo approccio di calcolo è basato sull’ipotesi dell’intensità dello sforzo di taglio e confronta gli sforzi dovuti al contatto e gli sforzi residui con la resistenza del materiale derivata dalla durezza locale. Witzig [18] ha eseguito estesi studi sperimentali sugli ingranaggi con modulo 3 mm e su altri ingranaggi con modulo 5 mm e interasse 200 mm.

I rispettivi limiti di fatica a TFF sono stati determinati per differenti materiali e proprietà. Witzig ha osservato che la TFF mostra un comportamento che segue una curva di Wöhler così come gli altri modi di cedimento a fatica.

La TFF si verificava prevalentemente sulla ruota condotta, ma anche principalmente sul pignone condotto quando la direzione del carico veniva invertita. Le cricche nucleavano a una profondità di 1,5-2 volte la CHD per le differenti CHD. Nel documento sono investigati anche i principali fattori di influenza, quali gli sforzi residui. Sulla base delle indagini sperimentali, è stato derivato un metodo di calcolo pratico [4, 10, 19] a partire dall’approccio di Oster [17] estendendolo ulteriormente.

Questo metodo di calcolo pratico costituisce la base della ISO/TS 6336-4. Weber [20-22] ha indagato estesamente dal punto di vista teorico il calcolo a TFF. Le sue ricerche hanno portato a un metodo di calcolo basato sull’approccio alla fatica basato sul piano critico. Oltre agli sforzi derivanti dalla deformazione del dente, sono considerati anche gli sforzi residui e vengono sviluppati i conseguenti approcci al calcolo. La resistenza del materiale si basa sulle ipotesi di Murakami [23], che tiene conto dell’influenza dei difetti del materiale.

La TFF è stata studiata dal punto di vista teorico e sperimentale anche nei lavori di Konowalczyk [24, 25], con ingranaggi di modulo 8 mm e interasse di 200 mm. Tuttavia, le varianti di ingranaggi considerate cedevano parzialmente per pitting. In tutti i casi di TFF si trovava una inclusione non metallica nel punto di nucleazione. La profondità del punto di nucleazione sotto la superficie del fianco attivo risultava indipendente dal carico.

Oltre ai risultati delle prove, viene anche presentato un approccio di calcolo basato sulle inclusioni. Nel progetto FVA 293 IV [26] è stata indagata l’influenza del grado di pulizia del materiale sulla resistenza a fatica a flessione ed è stata condotta qualche prova aggiuntiva sulla TFF. Sono stati sottoposti a prova ingranaggi con modulo 3 mm e interasse a = 200 mm, realizzati in 18CrNiMo7-6 ad alto grado di pulizia ed elevato coefficiente di strizione.

I risultati del progetto indicano un limite a TFF significativamente più alto rispetto ai precedenti risultati di Witzig con un usuale 18CrNiMo7-6. Ulteriori indagini teoriche e sviluppi degli approcci di calcolo relativi alla TFF sono descritti in svariati lavori. Vari autori hanno pubblicato importanti contributi alla comprensione dei meccanismi di questa modalità di cedimento [27-34].

Tuttavia, a confronto delle altre modalità di cedimento, quali il pitting e la rottura al piede, la TFF con nucleazione sotto la superficie è stata poco indagata e solo alcune campagne sperimentali sistematiche sono state pubblicate. Fino ad oggi, gli ingranaggi utilizzati sono solo con interasse di 200 mm. Riguardo alla TFF nelle applicazioni reali, le storie di carico sono in gran parte sconosciute e ciò rende impossibile replicare mediante calcolo teorico una TFF osservata sul campo. Sulla base delle sperimentazioni disponibili, sono già stati individuati i principali fattori di influenza sulla TFF.

Quelli determinanti sono il carico e più specificamente la pressione di contatto, la geometria (in particolare il raggio di curvatura relativa), gli sforzi residui e la resistenza del materiale. Siccome un più elevato valore del raggio di curvatura relativa porta il massimo sforzo di taglio a profondità più elevata, ingranaggi con grandi raggi di curvatura relativa sono più esposti alla TFF, la quale si verifica a profondità dove si hanno sforzi più bassi e resistenza del materiale minore.

La resistenza del materiale, la sua qualità e gli sforzi residui ad elevata profondità hanno un’influenza significativa sulla TFF. Tuttavia, I fattori di influenza relativi al materiale, quali il trattamento termico e il grado di pulizia e molti altri non sono ancora stati sufficientemente indagati dal punto di vista sperimentale.

Calcolo del rischio di TFF secondo ISO/TS 6336-4

Il metodo di calcolo della ISO/TS 6336-4 [3] è un metodo pratico non iterativo basato sull’approccio derivato da Witzig [18] dal modello di calcolo di più alto livello che fu sviluppato da Oster [17] e che è stato continuamente esteso.

L’approccio di Witzig è stato confrontato con il modello di più alto livello in 1,6 milioni di casi di calcolo e verificato per pressioni Hertziane p_H= 500-3000 N/mm², raggi di curvatura relativa ρ_rel = 5-150 mm e CHD di 0,3-4,5 mm. L’approccio della ISO/TS 6336-4 è stato validato con prove sperimentali al banco e su ingranaggi di diversa taglia di svariate applicazioni.

Le principali influenze sulla TFF considerate nel metodo di calcolo sono la pressione di contatto, il raggio di curvatura relativo, il profilo degli sforzi residui (solo di compressione per ora) e il profilo di durezza. L’approccio si basa sul confronto locale dello sforzo con la resistenza del materiale, che si traduce in una esposizione locale del materiale. L’esposizione locale del materiale viene calcolata per una certa profondità in direzione normale al fianco caricato per un punto di contatto della linea di condotta.

È stata definita l’esposizione locale del materiale ammissibile a TFF: per un’esposizione di ≈ 0,8 a profondità del materiale maggiore di 1 ∙ b_H, la probabilità di cedimento a TFF è approssimativamente del 50%.

Una esposizione del materiale più elevata nelle zone più vicine alla superficie non indica un più elevato rischio di TFF ma un più elevato rischio di cedimento superficiale: tuttavia il metodo non fornisce una verifica quantitativa per il pitting o altri danneggiamenti prossimi alla superficie, a causa di alcune significative semplificazioni relative allo stato di sforzo in superficie [18]. Nel seguito, le interrelazioni e i fattori di influenza sono descritti in maggior dettaglio. Gli sforzi sottosuperficiali dipendono principalmente dalla geometria delle dentature e dal carico applicato.

Sulla base della teoria Hertziana, gli sforzi sottosuperficiali di contatto sono proporzionali alla semiampiezza b_H e alla pressione di Hertz p_H. Al crescere del carico gli sforzi sottosuperficiali aumentano e il massimo sforzo di taglio si sposta a maggiore profondità. Anche per un più grande raggio di curvature relativa ρ_red, il massimo sforzo di taglio si trova a una maggiore profondità sotto il fianco attivo.

Il raggio di curvatura relativa nel punto primitivo C, ad esempio, può essere aumentato con un maggior angolo di pressione ⍺_n, mentre invece la pressione di Hertz in superficie diminuisce aumentando l’angolo di pressione. Elevati sforzi residui di compressione nella zona sotto la superficie dal fianco possono prevenire la nucleazione e spostare la massima esposizione a più elevate profondità nel materiale. Lo stato di sforzo residuo di compressione viene aggiunto allo stato di sforzo e la somma è confrontata con la resistenza del materiale.

La resistenza locale del materiale è derivata dal profilo di durezza in funzione della profondità con un fattore di influenza dipendente dal materiale base. Il profilo di durezza, che è usualmente descritto dalla CHD, dalla durezza in superficie (SH) e la durezza a cuore (CH) è pertanto decisivo per il profilo di resistenza che combinato con il profilo degli sforzi complessivi si traduce nel profilo di esposizione del materiale.

Riassumendo, il profilo di esposizione del materiale è attualmente basato sulla geometria di dentatura, sul carico e sul profilo di durezza con la profondità, insieme al profilo degli sforzi residui. Ulteriori fattori di influenza aggiuntivi sulla TFF, quali inclusioni non metalliche di diversa dimensione [34] e sforzi residui di trazione a profondità più elevate, possono essere considerati nel metodo secondo ISO/TS 6336-4 ma non sono ancora inclusi.

I valori ammissibili di resistenza a TFF come quelli della flessione (σ_{F lim}) o del pitting (σ_{H lim}) non sono ancora disponibili e ad oggi non è possibile il calcolo di una vita di servizio, perché non sono ancora stati fatti abbastanza studi sperimentali.

Obbiettivo della ricerca

Lo scopo di questa ricerca è lo sviluppo di un nuovo ingranaggio di prova che consenta di effettuare una sperimentazione economicamente conveniente sulla TFF. Fino ad oggi, gli ingranaggi di prova per la TFF erano ingranaggi di grandi dimensioni con interasse a = 200 mm e si avvertiva quindi la necessità di progettare un ingranaggio più piccolo.

Per il progetto di tale ingranaggio sono stati scelti i metodi standard della ISO 6336. In seguito a studi di progetto parametrici utilizzando l’approccio della ISO/TS 6336-4, è stato scelto e costruito un ingranaggio ad elevato rischio di TFF. L’ingranaggio di prova è quindi stato testato con prove di carico.

I risultati delle prove e la documentazione delle proprietà delle ruote dentate sono stati utilizzati per validare l’approccio di calcolo e per eseguire ulteriori indagini sul cedimento a TFF e sui suoi fattori di influenza.

Studi teorici e progetto degli ingranaggi di prova

Lo scopo delle indagini teoriche era quello di individuare un ingranaggio a denti diritti con un interasse di 91,5 mm, avente un elevato rischio di avaria a TFF e sufficienti margini rispetto alle altre modalità di cedimento.

L’interasse 91,5 mm consente prove economicamente vantaggiose utilizzando banchi a ricircolo di potenza standard [36]. Per assicurare un elevato rischio di cedimento a TFF e un basso rischio rispetto agli altri, sono stati utilizzati i calcoli della ISO 6336-2 [37] per la resistenza a pitting e della ISO 6336-3 [38] per la resistenza alla flessione.

Per determinare il rischio di TFF, è stato seguito l’approccio pratico della ISO/TS 6336-4.

Il punto di partenza dello studio teorico consisteva nelle svariate geometrie di ingranaggi di prova già esistenti. Inizialmente il progetto degli ingranaggi per la TFF fu basato su variazioni della geometria. Per le differenti geometrie, il rischio di TFF è stato analizzato facendo variare numerosi parametri, compresi il numero di denti o lo spostamento di profilo.

Le nuove varianti di ingranaggi sono state studiate teoricamente e verificate in termini del loro rischio a TFF, così come a pitting e a flessione. Gli ingranaggi selezionati sono stati poi ulteriormente indagati, facendo variare l’angolo di pressione e la microgeometria.

L’angolo di pressione è stato variato tra ⍺_n= 15° e ⍺_n= 25° per le geometrie scelte. Gli ingranaggi di prova più promettenti sono stati poi ulteriormente indagati τ dal punto di vista teorico (vedi tabella 1 per la geometria principale).

Come materiale per gli studi teorici è stato inizialmente scelto il 18CrNiMo7-6per la sua rilevanza per gli ingranaggi di grandi dimensioni, dovuta all’elevata temprabilità. Tuttavia, fu anche analizzato il 20MnCr5, materiale usuale degli ingranaggi di prova. La scelta del materiale influenza il profilo di resistenza τper(y) attraverso il fattore K_material. τ_per(y) è calcolato proporzionalmente al profilo di durezza con la profondità. Il profilo di durezza è stato calcolato con l’approccio di Lang [39], con variazioni della durezza in superficie, della durezza a cuore e della CHD.

È stato considerato l’approccio di Lang perché usualmente fornisce previsioni accurate de profilo di durezza per ingranaggi di piccole dimensioni. Si può calcolare il profilo di durezza anche secondo l’approccio di Thomas [40]. Questo approccio spesso dà una migliore previsione per gli ingranaggi grossi.

Inoltre, si può considerare il plateau di durezza in superficie che usualmente si osserva negli ingranaggi cementati di grosse dimensioni. Anche il profilo con la profondità degli sforzi residui è stato sempre calcolato sulla base del profilo di durezza con un approccio di Lang [39].

Studio parametrico sulla TFF secondo ISO/TS 6336-4

Sia la durezza che gli sforzi residui sono fattori di influenza rilevanti nell’approccio della ISO/TS 6336-4. Se il profilo degli sforzi residui è calcolato da quello della durezza, il profilo di durezza può avere un’influenza significativa sul profilo di esposizione del materiale A_TFF(y) come si vede per la geometria mostrata in figura 3.

Il profilo dell’esposizione del materiale con la profondità è calcolato con l’approccio di Lang e Thomas per una durezza in superficie rispettivamente di 735 HV e 680 HV e per una durezza a cuore rispettivamente di 320 HV e 450 HV. Per SH = 735 HV e una durezza a cuore di 450 HV i due approcci portano a a esposizioni massime assai differenti.

Con Lang la massima esposizione è minore di A_TFF= 0,6 e con Thomas è maggiore di A_TFF= 0,8. Tuttavia, l’influenza dei due approcci al calcolo della durezza sull’esposizione del materiale diminuisce con una minore durezza a cuore e in superficie come altrettanto mostrato in figura 3.

Una stima precisa del profilo di durezza con la profondità può migliorare l’accuratezza del calcolo della capacità di carico a TFF in modo significativo. Pertanto, si raccomanda caldamente di stimare il profilo di durezza in modo il più possibile accurato per poter verificare in modo attendibile il rischio di TFF.

La figura 4 mostra l’influenza della durezza superficiale sull’esposizione del materiale. La durezza del materiale è variata in un intervallo usuale per gli ingranaggi cementati. Il profilo di durezza e gli sforzi residui sono calcolati in accordo agli approcci di Lang. Si può vedere che per le durezze superficiali più basse il profilo di esposizione in prossimità della superficie differisce significativamente.

Tuttavia, l’esposizione del materiale alle profondità maggiori è meno influenzata. A profondità di circa 0,7 mm l’esposizione del materiale diviene comparabile. Se il profilo di durezza è calcolato con l’approccio di Thomas, si vede un aumento dell’esposizione del materiale per valori crescenti della durezza in superficie secondo quando mostrato in figura 5. In questo caso, si ha una pendenza più elevata e la transizione alla durezza a cuore è più vicina alla superficie con durezza superficiale più elevata.

Si ha anche un effetto sugli sforzi residui calcolati, che si traducono in una maggiore differenza nella massima esposizione del materiale calcolata. Con un calcolo dell’esposizione del materiale basata sull’approccio alla durezza di Thomas, una maggiore durezza superficiale porta a un più rischio di TFF teoricamente più elevato (e a una minore profondità dell’esposizione massima a causa dei differenti punti di transizione alla durezza a cuore).

Ciò non è validato sperimentalmente, ma non si può ancora escludere che una ripida diminuzione nella durezza dalla superficie al cuore della struttura possa indirettamente (per gli sforzi residui) avere effetti negativi sulla resistenza a TFF di una ruota dentata. La figura 6 mostra l’influenza della durezza a cuore sull’esposizione del materiale in accordo alla ISO/TS 6336-4.

Durezza a cuore significa, qui, la bassa durezza che si raggiunge sotto il fianco alle profondità più elevate. Se la durezza è calcolata con l’approccio di Lang, un aumento della durezza a cuore porta a una diminuzione del rischio di TFF, come usualmente ci si aspetta. Gli sforzi residui in profondità sono in questo caso comparabili. Se si varia la durezza a cuore nell’approccio di Thomas, l’influenza della durezza a cuore sull’esposizione del materiale differisce significativamente come mostrato in figura 7.

Il profilo di durezza fino a 0,5 mm è identico, ma la durezza a cuore e anche la profondità di transizione alla durezza a cuore cambiano con differenti valori di durezza a cuore. Ciò influenza gli sforzi residui e di conseguenza ha un impatto rilevante sull’esposizione del materiale calcolata. Per valori di durezza a cuore più alti la massima esposizione si sposta più vicino alla superficie del fianco.

Il valore massimo però non cambia. Invece, per resistenza più elevata nella zona del cuore ci si aspetterebbe usualmente un minore rischio di TFF. L’influenza teorica della CHD è mostrata in figura 8. Un aumento di CHD causa lo spostamento della durezza e degli sforzi residui verso profondità del materiale maggiori. Con l’aumento di CHD, il massimo rischio calcolato di TFF diminuisce molto e si sposta a profondità maggiori.

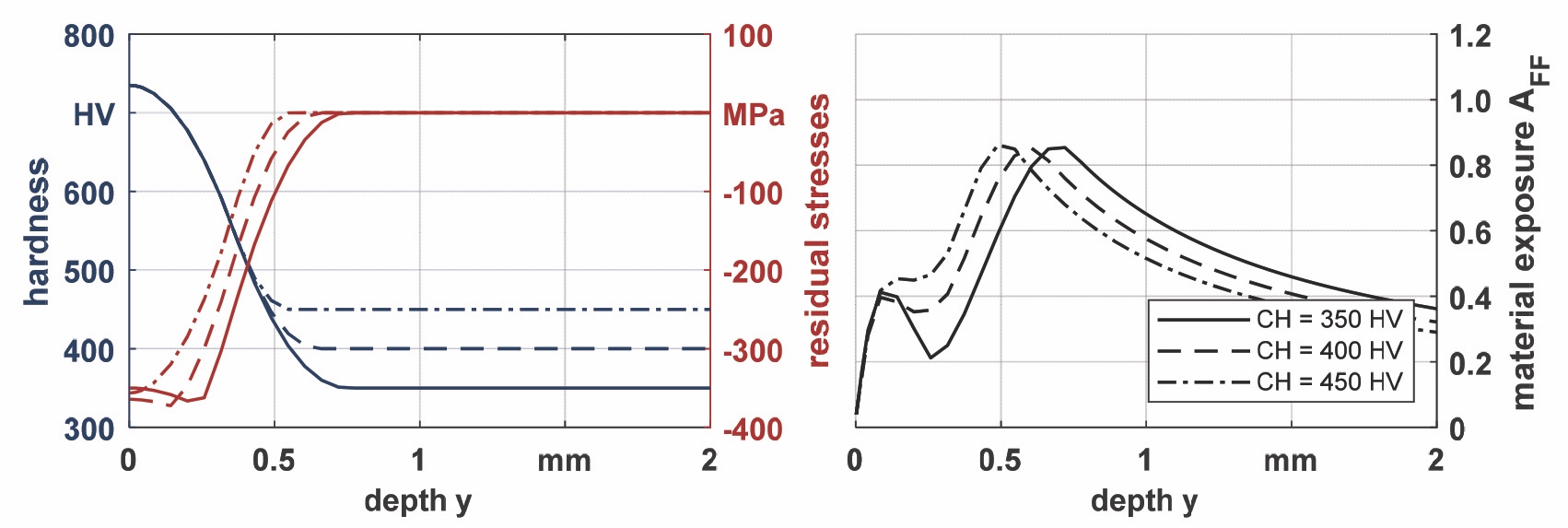
Anche se si calcola la durezza con l’approccio di Thomas si osserva una influenza confrontabile della CHD sull’esposizione del materiale. Anche l’entità della massima esposizione del materiale calcolata con i due approcci è la stessa per i tre valori di CHD considerati.

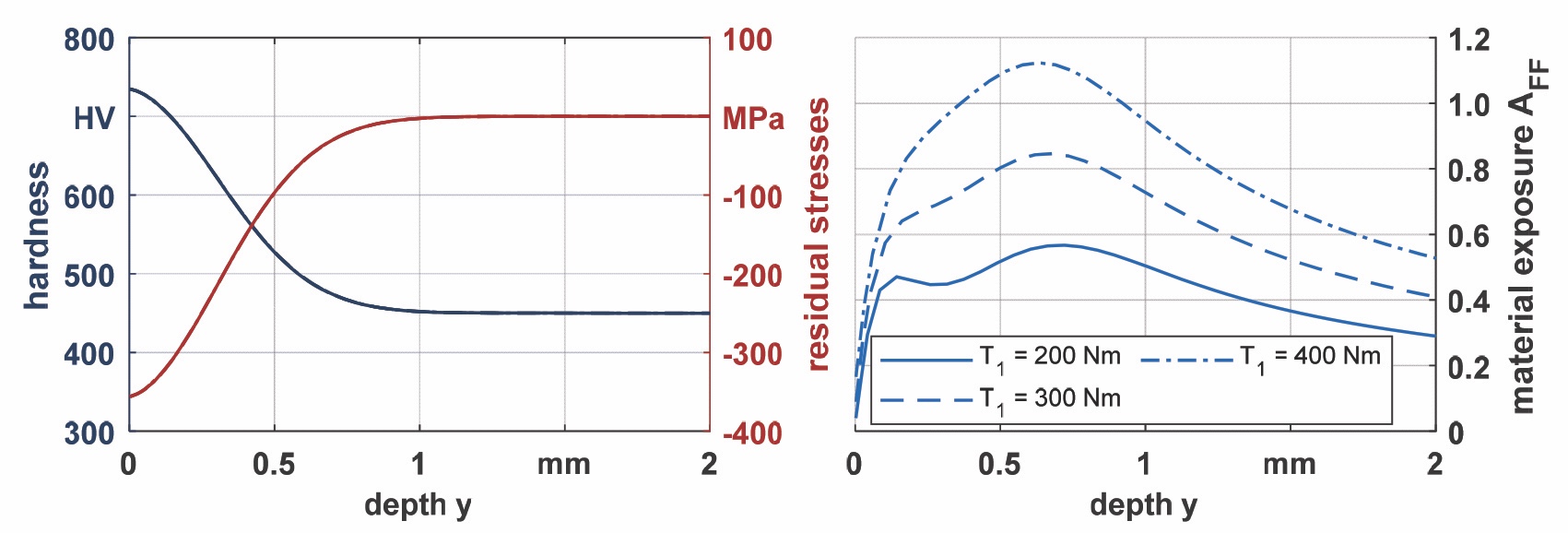
Naturalmente è stata anche indagata l’influenza della coppia sull’esposizione del materiale per l’ingranaggio di prova considerato come mostrato in figura 9. Le coppie T₁ = 200, 300 e 400 Nm sul pignone corrispondono rispettivamente a sforzi di contatto Hertziani pari a p_dyn = 1160, 1420, e 1640 N/mm². Per questa geometria la massima esposizione del materiale è a una profondità di circa y = 0,6-0,7 mm.

Per i diversi carichi, l’esposizione del materiale aumenta proporzionalmente. Tuttavia, la profondità della massima esposizione è confrontabile per i diversi carichi. Questo studio parametrico mostra che la durezza e gli sforzi residui hanno effetti significativi sulla esposizione del materiale calcolata, soprattutto alle profondità maggiori. Questi effetti possono risultare diversi a seconda che la durezza sia calcolata con l’approccio di Lang o di Thomas.

Con l’approccio di Thomas, l’esposizione del materiale aumenta all’aumentare della durezza in superficie o a cuore, cosa che non è confermata dalla sperimentazione e neppure ci si aspetta che lo sia. Il calcolo della durezza di Lang sembra più adatto per gli studi parametrici relativi al rischio di TFF. Nella ISO/TS 6336-4, si raccomanda di utilizzare profili di durezza misurati, opportunamente mediati e lisciati.

Altrimenti si potrebbe adattare il profilo di durezza calcolato al profilo di durezza atteso. L’importante è che il profilo di durezza con la profondità sia il più preciso possibile. Oltre alla geometria e la coppia, o la conseguente pressione di Hertz, il maggior fattore di influenza sull’esposizione del materiale calcolata è il raggio di curvatura relativa.

Al crescere della CHD usualmente il rischio di TFF diminuisce significativamente. Pertanto, è stata specificata una bassa CHD < 0,4 mm per la geometria di ingranaggio scelta. La CHD ottimale per la flessione è usualmente circa pari a 0,1-0,2 ∙ m_n [41], che per questo ingranaggio sarebbe 0,3-0,6 mm.

Anche la CHD ottimale per il pitting è funzione del raggio di curvatura relativa secondo [15] e sarebbe circa 1,2 mm per questo ingranaggio. Invece non è ancora stata effettuata un’indagine sperimentale sulla CHD ottimale per la TFF.

Calcolo della resistenza a pitting e a flessione a piede dente

Per l’ingranaggio di prova e la microgeometria scelti sono stati effettuati calcoli aggiuntivi relativi alla resistenza a flessione a piede dente e a pitting in accordo alle ISO 6336-2 [37] e ISO 6336-3 [38].

La figura 10 mostra I risultati del calcolo per l’ingranaggio progettato relativi alla capacità di carico a TFF, pitting e flessione a piede dente per larghezze di fascia di 13 mm e 20 mm. Per il calcolo con la ISO 6336, la coppia limite è stata determinata per un fattore di sicurezza unitario (S_H = 1.0, S_F = 1.0).

Riguardo alla TFF, è indicata la coppia corrispondente a un’esposizione del materiale A_FF = 0,8. Per calcolare le coppie limite, è stato necessario fare delle ipotesi per alcuni fattori della ISO 6336, quali Y_S (fattore di correzione dello sforzo) o Z_H (fattore di zona).

Gli sforzi limite, ad esempio, sono stati posti pari a σ _HP,ref = 1500 MPa e σ _FP,ref = 1080 MPa, che sono valori tipici per ingranaggi confrontabili che sono stati oggetto di sperimentazione presso l’istituto.

Tutti i risultati sono mostrati solamente per la ruota. Quelli del pignone sono confrontabili e non sono pertanto mostrati.

In figura 10, la coppia limite stimata per la TFF è 300 Nm. Sebbene Witzig [18] abbia mostrato che anche la TFF ha una curva S-N, non ci sono ancora sufficienti dati sperimentali per determinare una resistenza a fatica a termine, cioè per una vita finita. Un’esposizione del materiale A_TFF = 0,8 usualmente è correlata con una probabilità di cedimento del 50% al banco prova.

Per le coppie più elevate (≥ 600 Nm), si vede che i limiti di resistenza a pitting e a flessione si raggiungono dopo alcuni milioni di cicli di carico. Misure aggiuntive sono state pertanto prese per prevenire queste modalità di cedimento in modo affidabile nel corso delle prove. Per assicurare un alto fattore di sicurezza a pitting e per prevenire rotture a flessione nel corso delle prove, sono state considerate ruote dentate con spallamento per gli ingranaggi scelti [15].

Grazie all’allargamento della larghezza di fascia al raccordo al piede, si ottiene una maggiore resistenza a flessione senza influenzare la capacità di carico della superficie o la coppia necessaria per le prove. Si può ipotizzare, sulla base dell’esperienza delle prove disponibili, che la larghezza di fascia al piede è determinante per la capacità di carico a flessione. Per questa ragione, il dente è allargato al di sotto del fianco attivo fino alla larghezza di 20 mm, mentre la larghezza nel fianco è 13 mm.

La resistenza a pitting può essere aumentata riducendo la rugosità del fianco, con la pallinatura (shot peening) e la burattatura, così come con un lubrificante che con buone proprietà per la resistenza a pitting. Per evitare possibili maggiori costi di produzione, è stata specificata una rugosità più bassa per il processo di rettifica ed è stato scelto per le prove un olio con elevate proprietà per la resistenza a pitting.

Setup sperimentale, banco prova e attrezzatura di misura

Geometria, produzione e materiale degli ingranaggi di prova

Sulla base degli studi teorici secondo l’approccio della ISO/TS 6336-4, è stato progettato e costruito un ingranaggio di prova teoricamente incline alla TFF. La geometria scelta è mostrata in tabella 1.

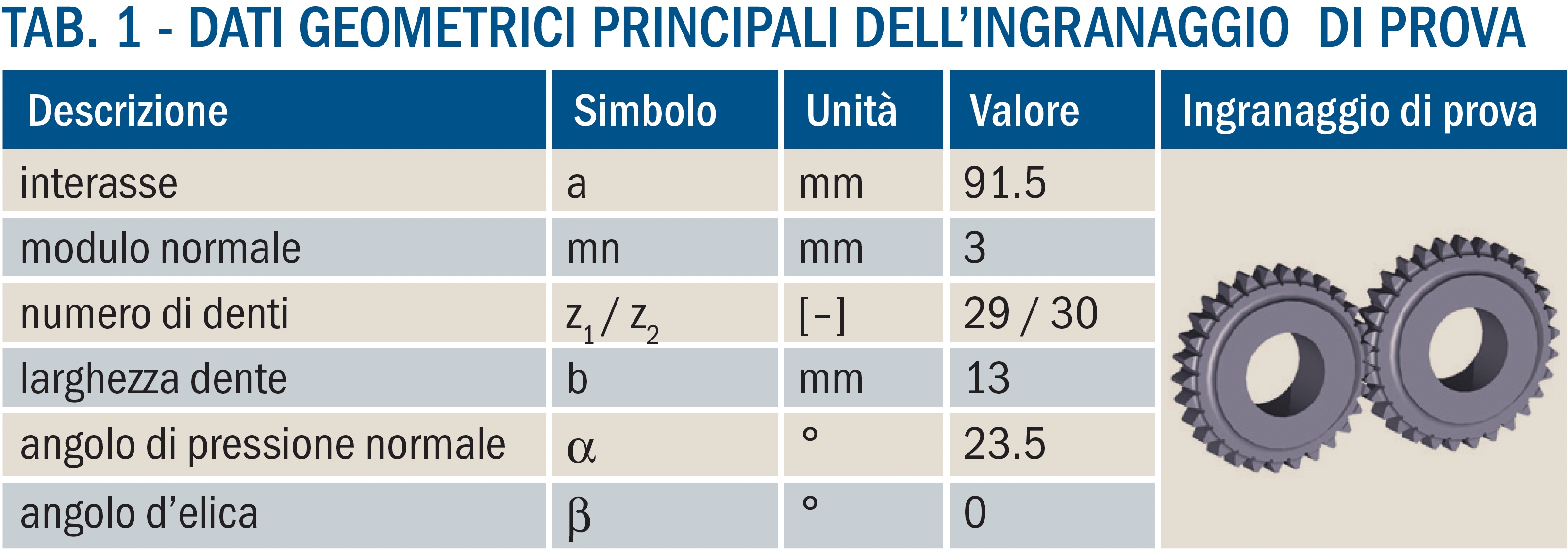Gli ingranaggi sono stati tagliati con una protuberanza di 0,15 mm da barre circolari laminate di 110 mm in 20MnCr5 (1.7147). Quindi è seguita una cementazione con la specifica di una massima CHD di 0,5 mm. Dopo il trattamento termico, gli ingranaggi sono stati puliti meccanicamente e un lotto è anche stato burattato.

Gli ingranaggi sono stati rettificati con una rettificatrice LGG 280, con una modifica di testa (tip Relief) di C_⍺a= 40 μm sui fianchi sia del pignone che della ruota. Il processo di rettifica è stato eseguito in due fasi, prerettifica e rettifica con velocità di 30-40 m/s. Con questo processo, l’effetto della protuberanza è stato quasi totalmente asportato per ottenere la CHD desiderata.

Banco e programma di prova

Le prove a fatica sono eseguite su un banco standard a ricircolo meccanico (back-to-back) con un interasse di 91,5 mm [42]. Questo banco ha un principio di ricircolo basato su un anello chiuso che collega un ingranaggio di prova e un altro ingranaggio uguale ma più largo in modo da applicare una coppia costante [36].

Il programma di prove è stato condotto in accordo alla direttiva FVA 563 I [43]. È stato provato un totale di 11 ingranaggi. L’obbiettivo era di generare cedimenti per TFF sui quali indagare le caratteristiche del cedimento. Obbiettivi ulteriori erano l’individuazione del ciclo di carico limite per determinare la resistenza a fatica a TFF e la verifica a fatica dell’ingranaggio.

Il pignone era conduttore della ruota e la velocità di rotazione e la coppia erano riferiti al pignone. La velocità di rotazione del pignone era n₁ = 3000 min_-1 per tutte le prove, tranne eseguita una a n₁ = 1500 min_-1.

Gli ingranaggi erano lubrificati a getto d’olio a 60°C con un olio sintetico di tipo PAO con un indice di viscosità ISO di 100. Questo lubrificante è stato scelto perché aveva già mostrato in altre prove elevate proprietà rispetto alla resistenza del fianco e sarebbe stato d’aiuto nel prevenire potenziali cedimenti per pitting.

Attrezzatura di misura

Per i profili di sforzi residui i campioni per le misure sono stati separati dagli ingranaggi con un processo che non generasse un impatto sugli sforzi residui.

La posizione di misura è al centro della larghezza di fascia e all’altezza del punto primitivo. Per la misura del profilo di durezza nella profondità, i singoli strati di materiale sono stati rimossi mediante attacco elettrochimico.

Gli sforzi residui in direzione tangente al profilo e assiale sono stati determinati con il metodo del sin2Ψ. Le misure sono state eseguite con un diffrattometro (Seifert XRD 3003 PTS) con radiazione cromo-K⍺ (40 mA e 40 kV) usando un foro collimatore del diametro di 1 mm, posto alla distanza di 10 mm dal punto di misura.

In ogni punto di misura è stato anche misurato il contenuto di austenite residua. La composizione chimica è stata determinata con uno spettrometro a emissione ottica.

La geometria dell’ingranaggio è stata misurata con un centro di misura 3D (P40 Klingelnberg). La microgeometria dei fianchi è stata misurata con un centro di misura per ingranaggi (P40). La rugosità del fianco è stata misurata con un dispositivo a contatto (T8000).

Risultati

Proprietà del materiale

Il materiale degli ingranaggi (20MnCr5 / 1.7147) è stato analizzato dopo la produzione. È stata analizzata la composizione chimica e la concentrazione media degli elementi è elencata in tabella 2. Le proporzioni tra gli elementi sono in accordo alle specifiche della norma DIN EN 10084 [45].

La pulizia del materiale degli ingranaggi è stata analizzata risguardo alle inclusioni non metalliche secondo le specifiche di prova per gli acciai (SEP) 1571, parti da 1 a 3 [46]. Si fa una distinzione tra cinque tipi di inclusioni non metalliche Tipo A (MnS), Tipo B (Al₂O₃), Tipo C (SiO₂), Tipo D (Al₂O₃) e Tipo D (CaS). Per la determinazione del grado di pulizia, sono state fatte sei diverse micrografie e valutate rispetto alla quantità dei differenti tipi di inclusione sulla superficie della micrografia.

I risultati sono mostrati in tabella 3. Gli ingranaggi avevano solo inclusioni di piccole dimensioni, che danno luogo a K4 = 0 per i solfuri e K4 = 30 per gli ossidi.

Geometria e rugosità del fianco

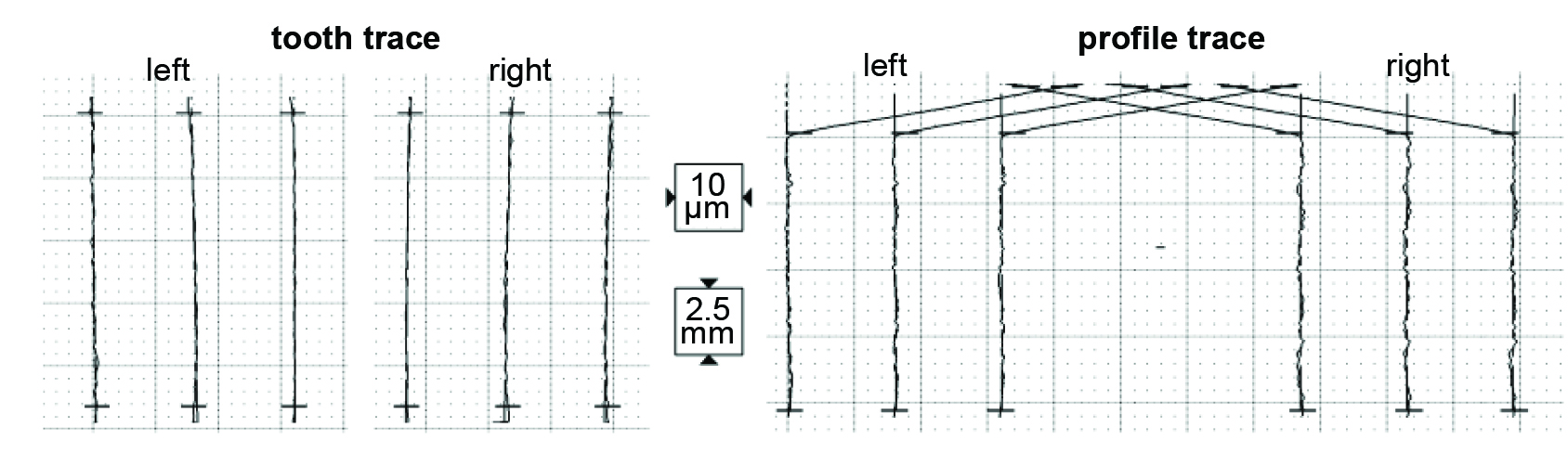
La geometria delle ruote dentate è stata misurata prima delle prove per determinare la qualità delle dentature secondo DIN 3962 [47]. Tutti gli ingranaggi hanno un grado di qualità Q ≤ 5. Il profilo e l’elica sono stati misurati su tre denti distanziati lungo la circonferenza per tutti gli ingranaggi.

Tutti gli ingranaggi hanno mostrato profili confrontabili e simili a quelli mostrati in figura 11. Nelle misure del profilo si nota la presenza del tip relief.

È stata misurata la rugosità dei fianchi destri oggetto di prova. Le misure restituiscono una rugosità media Ra ≈ 0,3 μm (Ra_min = 0,28 μm, Ra_max = 0,43 μm). Per l’ingranaggio sottoposto a burattatura la rugosità è Ra ≈ 0,06 μm.

Durezza

Dopo la prova è stato misurato il profilo di durezza su pignone e ruota. La durezza Vickers è stata misurata su entrambi I fianchi, in direzione normale al fianco partendo dal punto primitivo con HV 1 e HV 0,5 fino a una profondità di 1,2 mm.

La figura 12 mostra i profili di durezza misurati del fianco destro sottoposto a prova per il pignone e la ruota della prova No. 1. I fianchi sinistri (non oggetto di prova) mostrano profili simili.

Sono anche mostrati i profili di durezza calcolati con gli approcci di Lang [39] e Thomas [40], usualmente utilizzati in fase di progetto per ottenere profili di durezza appropriati per ingranaggi di piccole dimensioni. La correlazione tra i valori misurati e i profili determinati con l’approccio di Lang è assai buona.

Sforzi residui e austenite residua

La figura 13 mostra i profili di sforzi residui di entrambi i fianchi (caricato e non caricato) del pignone e della ruota dopo una prova a T₁= 500 Nm. I profili sono misurati fino a profondità diverse. Gli sforzi residui di pignone e ruota dovrebbero essere confrontabili a causa delle geometrie simili e del trattamento termico identico. Le differenze tra gli sforzi residui di pignone e ruota sono attribuibili all’usuale dispersione delle misure.

Si nota chiaramente una differenza tra i profili di durezza del fianco caricato e non caricato nella zona prossima alla superficie. Gli sforzi residui in superficie tendono a essere più elevati a causa del carico e raggiungono valori di circa -1300 MPa. In prossimità della superficie (0,05-0,15 mm) gli sforzi residui del fianco caricato sono più alti di quello scarico. Questo cambiamento negli sforzi residui è già stato osservato e descritto in [48].

A profondità di 0,15-0,6 mm, non vi è una differenza evidente tra i fianchi carico e scarico. Gli sforzi residui variano tra -100 MPa e -500 MPa. A profondità maggiori di 0,6 mm, gli sforzi residui assiali tendono a essere lievemente maggiori di quelli tangenziali e il fianco caricato della ruota mostra sforzi residui di compressione più elevati.

Non è stato applicato nessun fattore di correzione nella misura dei risultati, quale quello di Moore e Evans [49]. La correzione considera l’influenza della rimozione del materiale sugli sforzi residui che permangono. Con la correzione gli sforzi residui alle profondità più elevate sarebbero di minore compressione o anche di trazione.

Le misure di austenite residua non sono qui riportate. Comunque, le misure hanno dato valori usuali di austenite residua. L’austenite residua in prossimità della superficie è tra 10% e 25%. A profondità maggiori di 0,35 mm non è stata rilevata alcuna austenite residua.

Risultati delle prove

Undici coppie di ruote dentate sono state provate in un banco a ricircolo fino al verificarsi del cedimento o le prove sono state interrotte al raggiungimento di un numero di cicli molto elevato. Sono state quindi analizzate le caratteristiche del cedimento e la nucleazione della cricca primaria. Inoltre, le superficie di frattura dei singoli denti sono state analizzate al SEM.

La figura 14 mostra la foto del cedimento della prima prova. A sinistra si vede il dente fratturato, che mostra le tipiche caratteristiche della TFF. La cricca primaria è accompagnata da una cricca secondaria e una terziaria.

È anche visibile la conseguente rottura del dente vicino perché il banco non è stato arrestato immediatamente al verificarsi della TFF. Nell’immagine al centro si vede che la cricca primaria parte con un angolo di circa 50° rispetto al fianco e finisce con un’ampia curva in profondità del materiale, in corrispondenza del raccordo al piede sul fianco opposto. L’immagine a destra mostra la zona di frattura, nella cui parte sinistra si vede chiaramente il fisheye.

La figura 15 mostra i risultati delle 11 prove in un diagramma di Wöhler. Le prove sono state condotte a coppie da T₁ = 300 Nm fino a T₁ = 600 Nm. I cedimenti a TFF sono stati osservati tra N = 7 milioni e N = 70 milioni di cicli di carico. Due prove sono state interrotte al raggiungimento di un numero di cicli oltre il quale, sulla base dei primi esperimenti, non ci si aspettava più il cedimento. I due test superati sono a T₁ = 300 Nm e T₁= 400 Nm.

A T₁ = 350 Nm, che è presumibilmente prossimo al limite di fatica, si sono verificati due cedimenti prematuri. Si è ipotizzato che ciò dipendesse dalla presenza di grosse inclusioni non metalliche o da cluster di impurità, come è poi stato confermato dalle successive ispezioni (fig. 18).

Per le prove alle coppie più elevate, sono state scelti gli ingranaggi con la rugosità più bassa di Ra ≈ 0,3 μm. Tuttavia, le prove a T₁ = 600 Nm hanno mostrato la TFF e un concomitante danneggiamento simile al pitting, ad eccezione delle prove sull’ingranaggio sottoposto alla burattatura aggiuntiva (BF – barrel finishing).

Per gli ingranaggi provati a T₁= 500 Nm con una rugosità lievemente più alta (Ra ≈ 0,4 μm), non è stato osservato danneggiamento a pitting. Una prova (indicata con n) è stata condotta con n1=1500 min^-1, per indagare l’influenza della velocità di rotazione sulla TFF. Questa prova (n) non evidenzia un’influenza della velocità di rotazione sulla TFF. E comunque non ci si aspettava tale influenza, così come non vi è per gli altri cedimenti a fatica.

Il cedimento a TFF si è verificato prevalentemente sulla ruota condotta ad eccezione delle prove a T₁= 600 Nm, che hanno mostrato danneggiamenti aggiuntivi simili al pitting e una prova a T₁= 500 Nm. Inoltre, c’è la rottura fondamentalmente conseguente di almeno un dente vicino, perché il banco non viene fermato immediatamente quando la TFF avviene.

Per i pignoni provati a T₁ = 600 Nm, si è verificato un danneggiamento superficiale simile al pitting solamente sui fianchi del dente rotto e di quello vicino. I danneggiamenti simili al pitting sono prevalentemente posizionati sull’intera area dei due denti. Il pitting si osserva usualmente negli ingranaggi cementati e usualmente distribuito in modo uniforme sul dente nella parte di strisciamento specifico negativo. La figura 16 mostra il danneggiamento, le cui cause e tipologia sono ancora da determinare.

La figura 17 mostra un esempio di foto al microscopio elettronico a scansione (SEM) della superficie di frattura. L’immagine a sinistra è una visione d’assieme e quella destra è un ingrandimento del fisheye. Quasi tutte le superfici di frattura mostrano un fisheye evidente. Per la maggior parte delle prove il fisheye si mostra a lato sulla superficie di frattura. Il fisheye ellittico ha una lunghezza tra 3,2 mm e 6,2 mm e una larghezza tra 1,8 mm e 5,4 mm. Non è stata trovata una correlazione tra la coppia di prova e le dimensioni del fisheye.

Le analisi SEM e EDX (energy-dispersive x-ray) sono indispensabili per determinare con esattezza il punto di nucleazione e se vi sia una inclusione non metallica che ha causato la nucleazione. Per le due prove a T₁ = 350 Nm, si sospetta che il cedimento prematuro possa essere spiegato da una inclusione di grosse dimensioni o da un cluster di inclusioni piccole.

Per la determinazione del punto di nucleazione, bisogna esaminare visivamente un ingrandimento del fisheye [50]. Il percorso di propagazione o l’insieme delle cricche usualmente conducono a un’area di origine più piccola: la nucleazione è attesa in questa zona. Però spesso è difficile individuare il punto di nucleazione esatto. Tuttavia, in questa zona si possono trovare con le analisi EDX le inclusioni non metalliche, le impurità o i cluster.

Per le singole TFF, l’origine sottosuperficiale della cricca è stata ulteriormente indagata. Nella maggioranza dei casi, non sono state trovate inclusioni non metalliche nell’area di nucleazione. In un caso, è stata trovata una piccola inclusione di ossido di alluminio di circa 30 μm, ma si è potuto escludere che fosse il punto di nucleazione.

In figura 18 è mostrato l’esame della nucleazione della cricca per la prova a T₁= 350 Nm con una vita di circa 45 Mill. di cicli di carico. L’origine della cricca è stata analizzata al SEM e con ulteriori analisi EDX.

Dapprima si è analizzato il fisheye riguardo ai percorsi di propagazione e successivamente l’area di origine sospettata della cricca è stata ulteriormente oggetto di analisi EDX per la ricerca di inclusioni non metalliche. In questo caso, è stato trovato un cluster di inclusioni non metalliche, che costituiscono il punto di nucleazione presumibile. Le analisi EDX hanno mostrato un cluster di piccole inclusioni di ossido di alluminio di una lunghezza di circa 200 μm.

Conclusioni e prospettive

In questo lavoro è stato utilizzato il metodo di calcolo standard per la capacità di carico a frattura del fianco del dente (TFF) secondo la ISO/TS 6336-4 per progettare un nuovo ingranaggio di prova che può essere utilizzato per indagare la TFF in un banco prova standardizzato con interasse 91,5 mm.

Con studi parametrici sui fattori di influenza della ISO/TS 6336-4, si è messo in luce il loro effetto sul rischio calcolato di TFF. Inoltre, le TFF ottenute sono state caratterizzate e ulteriormente esaminate.

I risultati principali di queste ricerche sono sintetizzati nelle seguenti conclusioni:

• L’approccio della ISO/TS 6336-4 è idoneo a progettare ingranaggi di prova inclini alla TFF. E viceversa, l’approccio dovrebbe anche essere idoneo per prevenire la TFF.
• Le sensibilità del rischio calcolato di TFF al variare dei principali fattori di influenza può essere elevata. Nella fase di progetto, nella quale spesso si utilizzano approcci teorici per il calcolo della durezza e degli sforzi residui, piccole imprecisioni possono già portare a valutazioni significativamente fuorvianti del rischio di TFF.
• Il profilo di durezza secondo l’approccio di Lang mostra una buona correlazione con i valori medi di durezza misurati sugli ingranaggi di piccole dimensioni qui utilizzati. L’approccio di Thomas sembra più adatto per i bassi valori di durezza.
• Gli sforzi residui in prossimità della superficie sono influenzati dal carico. Alle profondità più elevate invece non vi è l’evidenza che il carico modifichi gli sforzi residui. Non si misurano sforzi residui di trazione fino a profondità di 1 mm. Tuttavia, non è stato considerato l’effetto della rimozione del materiale.
• Le caratteristiche della TFF già descritte in precedenza possono essere confermate. Inoltre, la superficie di frattura mostra il tipico fisheye, che ci si attende per i cedimenti con innesco sottosuperficiale.
• È stata confermata per la TFF la natura di cedimento a fatica con un comportamento alla Wöhler e i cedimenti prematuri sono stati causati da grosse inclusioni non metalliche, che hanno accorciato la vita.
• Cedimenti con origine in superficie o danneggiamenti simili al pitting possono essere prevenuti con la burattatura della superficie.

In seguito a ulteriori risultati di prova e indagini dei cedimenti, le singole TFF saranno oggetto di ricalcolo secondo la ISO/TS 6336-4 e sarà valutata l’accuratezza. La ricerca sulla TFF è ancora limitata e la specifica tecnica può già essere applicata anche se potrebbe avere bisogno di ulteriori estensioni o di fattori di influenza aggiuntivi per migliorare l’accuratezza.

Le estensioni dovrebbero essere definite sulla base di indagini sperimentali sulla TFF. Alcune influenze sulla TFF, quali l’influenza degli sforzi residui, l’effetto di differenti materiali base e di proprietà del materiale, quali le inclusioni non-metalliche o l’effetto del tipo di trattamento termico e dei suoi parametri, sono noti ma non sono ancora stati oggetto di sufficienti ricerche.

Alcuni suggerimenti per l’estensione del calcolo a TFF sono stati già sviluppati da differenti autori ma non sono ancora stati sufficientemente validati sperimentalmente. Inoltre, la statistica delle distribuzioni delle fratture o la specificazione di diverse probabilità di cedimento devono essere oggetto di ricerca sulla base di più diagrammi di Wöhler ottenuti da prove al banco su TFF.

Con l’ingranaggio di prova sviluppato, si possono eseguire in modo efficiente indagini sistematiche su molti altri fattori di influenza.

Ringraziamenti

Gli autori ringraziano lo studente Thomas Eckardt per le analisi teoriche sulla TFF svolte nella sua tesi semestrale così come Silke Rösch e Georgsmarienhütte GmbH per le analisi SEM delle superfici di frattura.

Articolo tratto da una relazione presentata all’AGMA FTM 2021 e stampato con l’autorizzazione dell’American Gear Manufacturers Association, proprietaria dei diritti d’autore. American Gear Manufacturers Association, 1001 N. Fairfax Street, 5th Floor, Alexandria, Virginia 22314. Le dichiarazioni e le opinioni espresse in questo testo sono quelle degli autori e non sono da considerarsi ufficiali dell’American Gear Manufacturers Association. Si ringrazia l’AGMA per la gentile autorizzazione alla pubblicazione (NdR).

Bibliografia

1. ISO 6336, 2016, “Calculation of load capacity of spur and helical gears”.
2. ANSI/AGMA 2101-D04, 2004, “Fundamental Rating Factors and Calculation Methods for Involute Spur and Helical Gear Teeth”.
3. ISO/TS 6336-4, 2019, “Calculation of load capacity of spur and helical gears – Part 4: Calculation of tooth flank fracture load capacity”.
4. Hein, M., Tobie, T., and Stahl, K., 2017, “Calculation of tooth flank fracture load capacity – Practical applicability and main influence parameters”, AGMA 2017 Fall Technical Meeting, Columbus, USA.
5. Boiadjiev, I., Stemplinger, J.-P., and Stahl, K., 2015, “New Method for Calculation of the Load Carrying Capacity of Bevel and Hypoid Gears regarding Tooth Flank Fracture”, VDI International Conference on Gears, Munich, Germany, pp.173–182.
6. Bauer, E., 1995, “Examples for Subsurface Initiated Gear Failures “ (published in german: “Beispiele für Verzahnungsschäden, ausgehend von innenliegenden Fehlstellen“). Antriebstechnik, Alianz Report 86, 6, pp.230-238.
7. Bauer, E., 1998, “Tooth Flank Fractures in High Performance Transmissions” (published in german: “Flankenbrüche bei Hochleistungsgetrieben”), Allianz Report 2/98”, pp.79-87.
8. Bauer, E. and Böhl, A., 2010, “Flank Breakage on Gears for Energy Systems”, VDI International Conference on Gears, VDI-Berichte Nr. 2108.
9. Al, B. C. and Langlois, P., 2016, “Analysis of Tooth Interior Fatigue Fracture Using Boundary Conditions from an Efficient and Accurate LTCA”, Gear Solutions, February 2016, pp.33–39.
10. Hein, M., Tobie, T., and Stahl, K., 2017, “Parameter study on the calculated risk of tooth flank fracture of case hardened gears”, JSME International Conference on Motion and Power Transmissions.
11. MackAldener, M. and Olsson, M., 2001, “Tooth Interior Fatigue Fracture – computational and material aspects”, International Journal of Fatigue, 23(4), pp.329-340.
12. MackAldener, M. and Olsson, M., 2002, “Analysis of crack propagation during tooth interior fatigue fracture”, Engineering Fracture Mechanics (69), pp.2147-2162.
13. Fuchs, D., Schurer, S., Tobie, T., and Stahl, K., 2019, “Investigations into non-metallic inclusion crack area characteristics relevant for tooth root fracture damages of case carburised and shot-peened high strength gears of different sizes made of high-quality steels”, Forschung im Ingenieurwesen, 83(3), pp.579–587.
14. Tobie, T., Stahl, K., and Höhn, B.-R., 2013, “Tooth Flank Breakage: Influences on Subsurface Initiated Fatigue Failures of Case Hardened Gears”, ASME 2013, Portland, Oregon, USA.
15. Tobie, T., 2001, “Influence of the case hardening depth on the pitting strength and tooth bending strength of larger gears” (published in german: “Zur Grübchen- und Zahnfußtragfähigkeit einsatzgehärteter Zahnräder”. Einflüsse aus Einsatzhärtungstiefe, Wärmebehandlung und Fertigung bei unterschiedlicher Baugröße”, Ph.D. thesis, FZG, Technical University of Munich, Germany.
16. Bruckmeier, S., 2006, “Tooth Flank Fracture in Gearings” (published in german:”Flankenbruch bei Stirnradgetrieben”, Ph.D. thesis, FZG, Technical University of Munich, Germany.
17. Oster, P., 1982, “Stresses in gears below the EHL contact” (published in german: “Beanspruchung der Zahnflanken unter Bedingungen der Elastohydrodynamik”, Ph.D. thesis, FZG, Technical University of Munich.
18. Witzig, J., 2012, “Tooth flank fracture – limit of load carrying capacity in the material depth” (published in german:”Flankenbruch – Eine Grenze der Zahnradtragfähigkeit in der Werkstofftiefe”, Ph.D. thesis, FZG, Technical University of Munich, Germany.
19. Boiadjiev, I., Witzig, J., Tobie, T., and Stahl, K., 2014, “Tooth Flank Fracture – Basic Principles and Calculation Model for a Subsurface Initiated Fatigue Failure Mode of Case Hardened Gears”, VDI International Conference on Gears, Lyon Villeurbanne, France, pp.670–680.
20. Weber, R., 2015, “Design concept against volume failure in case-hardened spur gears.” (published in german: “Auslegungskonzept gegen Volumenversagen bei einsatzgehärteten Stirnrädern”, Ph.D. thesis, University of Kassel, Germany.
21. Weber, R., Damerau, J., Rötting, J., and Bacher-Höchst, M., 2013, “Simulation of dynamic tooth loads and local stress histories in involute gears”, VDI International Conference on Gears, München, Germany.
22. Weber, R., Rötting, J., Scholtes, B., and Bacher-Höchst, M., 2014, “Load stresses and residual stresses in the tooth interior”, Lyon Villeurbanne, France, Woodhead Publishing, 2, pp.804–813.
23. Murakami, Y., 2019, “Metal Fatigue: Effects of Small Defects and Nonmetallic Inclusions. Elsevier Science & Technology, San Diego, Ann Arbor, Michigan.
24. Konowalczyk, P., 2018, “Grübchen- und Zahnflankenbruchtragfähigkeit großmoduliger Stirnräder”. „Pitting and tooth flank fracture load capacity of large modul spur gears”, Ph.D. thesis, Edition Wissenschaft Apprimus, Band 21/2018. Apprimus Verlag, Aachen.
25. Konowalczyk, P., Löpenhaus, C., and Brecher, C., 2017, “Inclusion Based Calculation Approach for Flank Fracture Load Capacity”, 58th Conference “Gear and Transmission Research” of the WZL on May 10/11.
26. Fuchs, D., Tobie, T., and Stahl, K., 2021, “Investigations on fisheye failures in gears and their Influence on the load carrying capacity” (published in german: “FVA 293 IV: Untersuchungen zum Fehlstellenversagen an Zahnrädern und deren Einfluss auf die Zahnradtragfähigkeit”, Forschungsvereinigung Antriebstechnik e.V.
27. Ghribi, D., Octrue, M., and Sainsot, P., 2015, “Comparative study of the tooth flank fracture in cylindrical gears. Efficient method to assess the risk of the tooth flank fracture on the cylindrical gears”, VDI International Conference on Gears, Munich, Germany.
28. Kampka, M., Brecher, C., and Löpenhaus, C., 2018, “Optimization of Power Density by Local Gear Failure Modeling”, AGMA Fall Technical Meeting.
29. Liu, H., Liu, H., Bocher, P., Zhu, C., and Sun, Z., 2018, “Effects of case hardening properties on the contact fatigue of a wind turbine gear pair”, International Journal of Mechanical Sciences, 141, pp.520-527.
30. Meis, J.-A., 2017, “Flank fracture assessment under consideration of material quality”, VDI International Conference on Gears, Munich, Germany.
31. Octrue, M., Ghribi, D., and Sainsot, P., 2017, “A Contribution to Study The Tooth Flank Fracture (TFF) In Cylindrical Gears”, 7th International Conference on Fatigue Design, 29-30 November, Senlis, France.
32. Sandberg, E., 1981, “A Calculation Method for Subsurface Fatigue. Det Norske Veritas (DNV)”, International Symposium on Gearing & Power Transmissions, Tokyo.
33. Wang, W., Liu, H., Zhu, C., Bocher, P., Liu, H., and Sun, Z., 2018, “Evaluation of Rolling Contact Fatigue of a Carburized Wind Turbine Gear Considering the Residual Stress and Hardness Gradient”, Journal of Tribology, 140(6), pp.61401:1-10.
34. Wickborn, C., 2017, “Extension of the flank load carrying capacity calculation of cylindrical gears in the material depth – influence of material properties and material defects” (published in german: “Erweiterung der Flankentragfähigkeitsberechnung von Stirnrädern in der Werkstofftiefe- Einfluss von Werkstoffeigenschaften und Werkstoffdefekten”, Ph.D. thesis, Technical University of Munich, Germany.
35. Iss, V., Müller, D., and Haupt, N., 2022 (ongoing), “Extended calculation of the tooth flank fracture risk of case-hardened gears with consideration of the residual stresses in larger material depths” (published in german: “FVA 835: Erweiterte Berechnung der Flankenbruchgefährdung einsatzgehärteter Zahnräder unter besonderer Berücksichtigung des Eigenspannungszustands in größerer Werkstofftiefe. Forschungsvereinigung Antriebstechnik e.V.
36. DIN 51354 Part 1, 1990, “Testing of lubricants; FZG gear test rig; general working principles”.
37. ISO 6336-2, 2006, “Calculation of load capacity of spur and helical gears – Part 2: Calculation of surface durability (pitting)”.
38. ISO 6336-3, 2006, “Calculation of load capacity of spur and helical gears – Part 3: Calculation of tooth bending strength”.
39. Lang, O. R., 1988, “Calculation and Design of Inductive Hardened Components” (published in german: “Berechnung und Auslegung induktiv randschichtgehärteter Bauteile. In: Kloos, K. H.; Grosch J.: Induktives Randschichthärten, 23.-25. March 1988, Munich: Arbeitsgemeinschaft Wärmebehandlung und Werkstofftechnik (AWT) conference Proceedings, pp. 332-348.
40. Thomas, J., 1998, “Load carrying capacity of bevel gears” (published in german: “Flankentragfähigkeit und Laufverhalten von hart-feinbearbeiteten Kegelrädern”, Ph.D. thesis, FZG, Technical University of Munich, Germany.
41. ISO 6336-5, 2016, “Calculation of load capacity of spur and helical gears – Part 5: Strength and quality of materials”.
42. DIN ISO 14635-1, 2006, “Gears – FZG test procedures – Part 1: FZG test method A/8,3/90 for relative scuffing load-carrying capacity of oils”.
43. Tobie, T. and Matt, P., 2012, “FVA Directive 563 I: Standardisation of Load Capacity Tests”.
44. König, J., Tobie, T., and Stahl, K., 2019, “Influences of Lubrication on Pitting Strength for Different Flank Conditions” (published in german: “FVA 459 III: Schmierstoffeinfluss Grübchentragfähigkeit. Schmierstoffeinflüsse auf die Grübchentragfähigkeit bei unterschiedlichen Flankenzuständen”, Forschungsvereinigung Antriebstechnik 1337.
45. DIN EN 10084, 2008, “Case hardening steels – Technical delivery conditions”.
46. SEP 1571, 2017, “Evaluation of inclusions in special steels based on their surface areas – parts 1-3”, publisher: Stahleisen GmbH, Düsseldorf, Germany.
47. DIN 3962, 1978, “Tolerances for Cylindrical Gear Teeth; Tolerances for Deviations of Individual Parameters”.
48. Elstorpff, M.-G., 1993, “Influences on pitting strength of case carburized gears up to the highest finite life” (published in german: “Einflüsse auf die Grübchentragfähigkeit einsatzgehärteter Zahnräder bis in das höchste Zeitfestigkeitsgebiet”, Ph.D. thesis, Technical University of Munich, Germany.
49. Moore, M. G. and Evans, W. P., 1958, “Mathematical Correction for Stress in Removed Layers in XRay Diffraction Residual Stress Analysis”, SAE Transactions, Vol. 66 pp. 340-345.
50. Fuchs, D., Rommel, S., Tobie, T., and Stahl, K., 2021, “In-depth analysis of crack area characteristics of fisheye failures in high-strength gears”, International Journal of Fracture – Open access (Springer).