La pallinatura è ampiamente utilizzata per migliorare il comportamento a fatica dei componenti metallici, grazie alla capacità di indurre indurimento superficiale e campi di tensioni residue compressive (Figura 1). Questi benefici, tuttavia, non sono garantiti in ogni condizione: se i parametri del processo non vengono selezionati correttamente, possono comparire effetti indesiderati che riducono la resistenza a fatica.
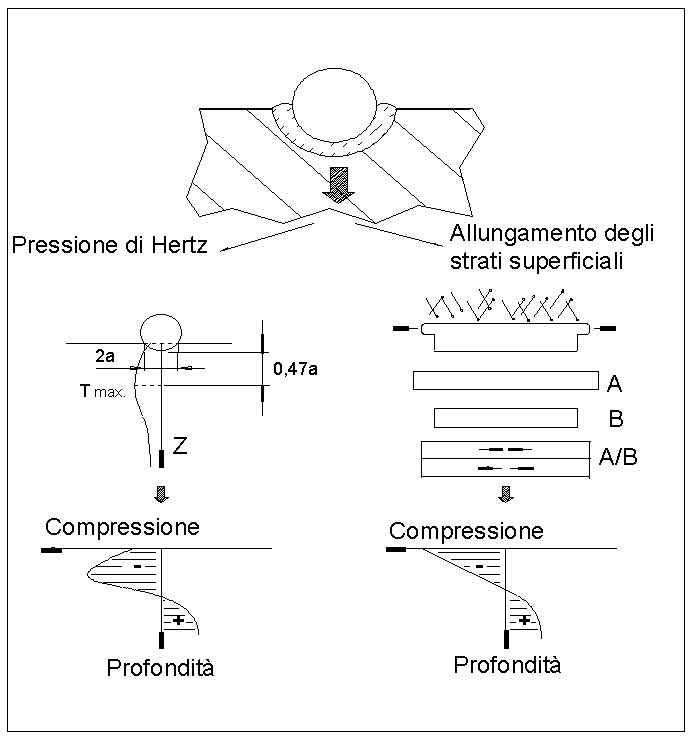
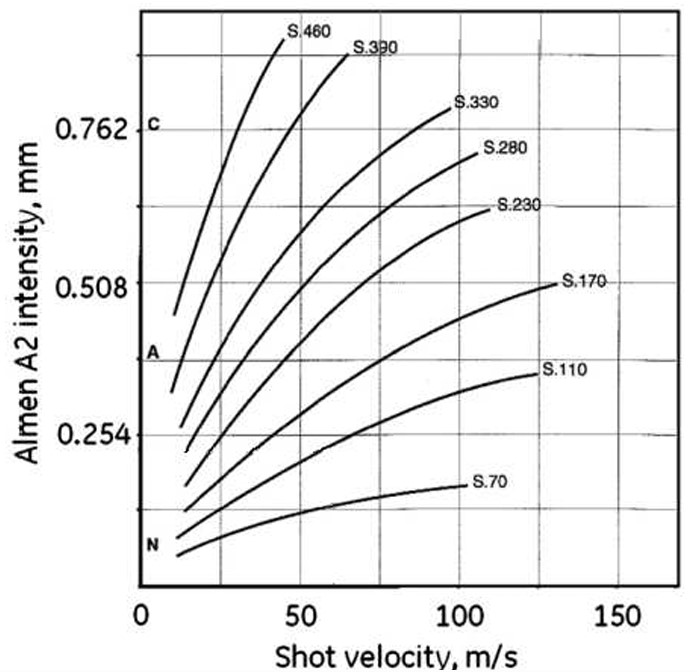
Il fenomeno della pallinatura, o shotpeening, è molto più complesso di quanto possa apparire a prima vista. In Figura 1b è schematizzato il meccanismo di contatto localizzato tra il pallino ed il materiale (pressione di Hertz) che provoca deformazioni plastiche e allungamento degli strati superficiali, generando così campi di compressione residua che si distribuiscono in profondità nel materiale. Nella stessa immagine è anche rappresento come il passaggio da un singolo ad una miriate di pallini modifichi in modo significativo il profilo di tensioni residue nel materiale. In Figura 1c invece è mostrato un esempio di come l’intensità dell’impatto (misurato convenzionalmente in Almen) è legato a fattori multipli, come, ad esempio, velocità e dimensione dei pallini. Anche solo attraverso questi semplici esempi si comprende immediatamente come nella pallinatura risulti essenziale comprendere l’influenza singola o combinata dei parametri di processo e riuscire a determinarne i valori ottimali.

Per farlo si possono impiegare approcci analitici, sperimentali o numerici. I metodi analitici offrono soluzioni semplificate ma non sempre applicabili a casi complessi, specie in presenza di geometrie e materiali meno comuni; le prove sperimentali forniscono dati importanti e reali ma richiedono tempo e risorse significative; le simulazioni numeriche, invece, permettono di ridurre i costi sperimentali offrendo modelli predittivi sempre più accurati.
Nel corso degli anni proprio utilizzando le simulazioni è stato spesso indagato l’effetto di parametri quali velocità e dimensione dei pallini, pressione, angolo d’impatto, tempo di esposizione, distanza dell’ugello e percentuale di copertura, arrivando talvolta a risultati interessanti anche in termini di ricadute pratiche. È stato osservato, ad esempio, che questi fattori possono modificare profondamente lo stato di tensione residua, la durezza superficiale e la rugosità, con ripercussioni dirette sulla vita a fatica e, in alcuni casi, anche su fenomeni di corrosione o bagnabilità dei materiali.
Molti studi poi si sono concentrati su singoli obiettivi – ad esempio massimizzare la durezza, ridurre la rugosità o aumentare la profondità delle tensioni residue – mentre meno ricerche hanno affrontato la ottimizzazione multi-obiettivo, cioè la ricerca simultanea delle condizioni che garantiscono il miglior equilibrio tra proprietà spesso in competizione. Inoltre, raramente è stato analizzato in modo sistematico l’effetto dello spessore del pezzo trattato, che può influenzare significativamente la distribuzione delle tensioni.
Da queste considerazioni nasce l’esigenza più generale di sviluppare modelli statistici integrati con simulazioni numeriche, capaci di descrivere in maniera affidabile il processo e guidare l’individuazione dei parametri ottimali, bilanciando tensioni residue e rugosità superficiale, con l’obiettivo finale di migliorare la durabilità dei componenti meccanici.
Materiali e metodi
Per analizzare e ottimizzare il processo di pallinatura nello studio internazionale qui riportato è stato utilizzato un approccio basato su simulazioni numeriche e strumenti statistici. L’idea di fondo è stata quella di ricostruire digitalmente l’impatto dei pallini sul materiale e, a partire dai risultati, costruire un modello che permettesse di prevedere le condizioni ottimali senza dover eseguire una quantità eccessiva di test reali (Figura 2).
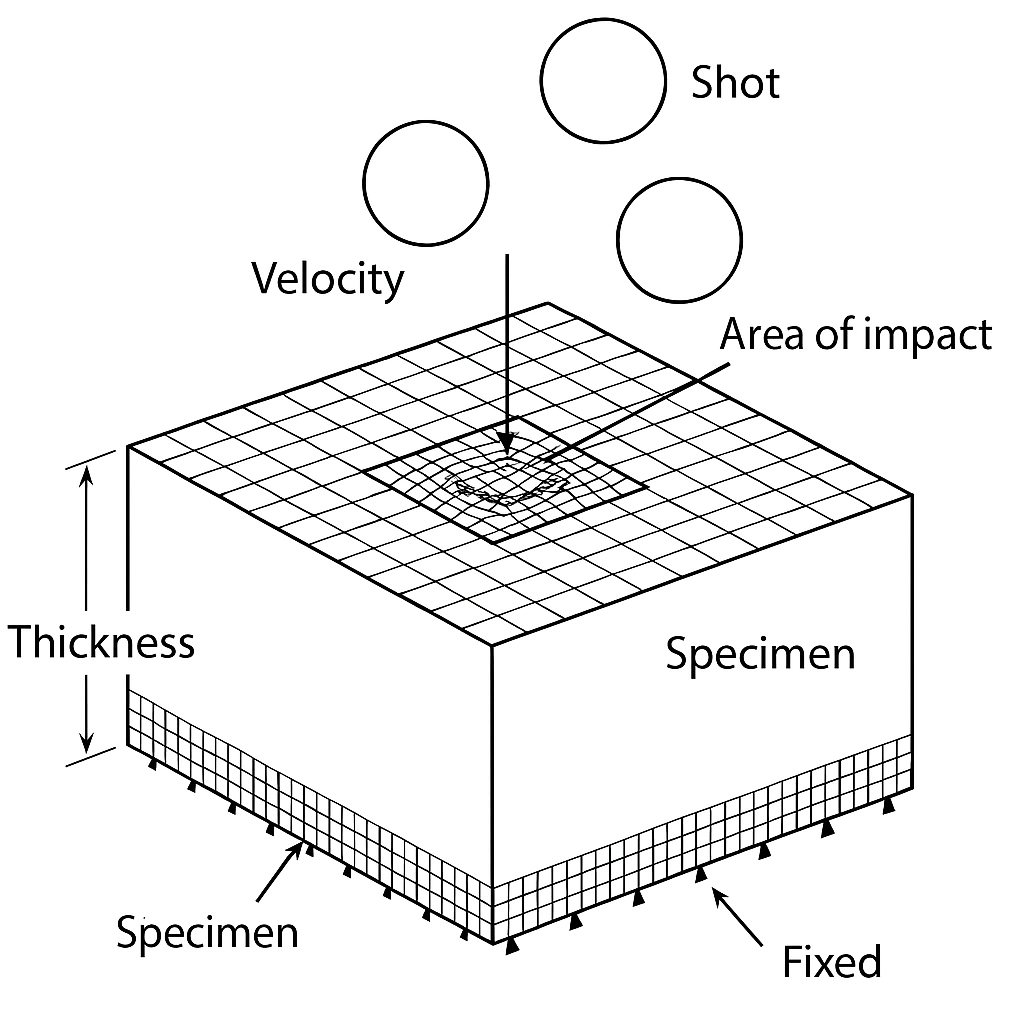
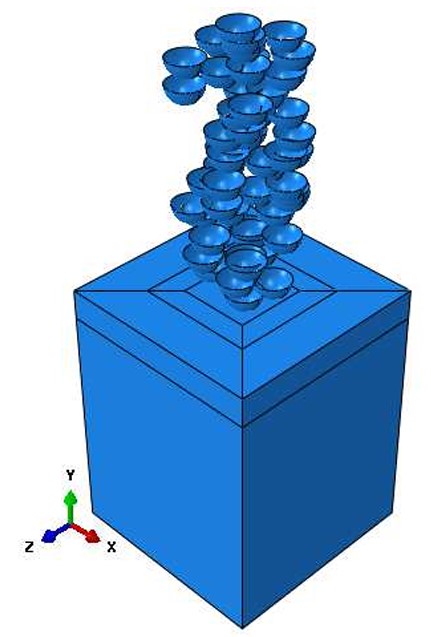
Le simulazioni sono state svolte con il software di analisi ABAQUS, impiegando un modello tridimensionale esplicito capace di catturare gli effetti dinamici dell’urto. L’obiettivo era simulare gli urti successivi dei pallini sulla superficie metallica, così da calcolare come si generano le tensioni residue e come varia la qualità superficiale del componente. Per ridurre le oscillazioni numeriche indesiderate sono stati introdotti opportuni coefficienti di smorzamento, in modo da ottenere risultati stabili e affidabili.
Il materiale considerato è stato un acciaio inox martensitico AISI 420, modellato con la legge costitutiva di Johnson-Cook, che descrive il comportamento plastico a seconda della deformazione, della velocità di deformazione e della temperatura (box 1). Questo modello è adatto a simulare urti rapidi e deformazioni intense come quelle della pallinatura. I pallini sono stati considerati rigidi, assegnando loro velocità iniziali variabili (70–110 m/s), mentre l’interazione tra pallino e superficie è stata modellata con attrito (coefficiente 0,2). La superficie è stata discretizzata con una mesh molto fine nella zona di impatto, per descrivere in dettaglio la formazione delle tensioni residue e delle deformazioni.
Per riprodurre condizioni realistiche, è stato introdotto un algoritmo di distribuzione casuale degli impatti, così da simulare l’effetto di più pallini in successione. In questo modo, il modello non si limita a descrivere un singolo urto ideale, ma approssima meglio la distribuzione irregolare tipica del processo reale.
Sono stati variati quattro parametri principali:
- diametro dei pallini,
- velocità di impatto,
- percentuale di copertura,
- spessore del provino.
Questi parametri sono stati combinati secondo un piano sperimentale di tipo statistico, o Design of Experiments (DoE), che consente di valutare non solo l’effetto di ciascun fattore, ma anche le possibili interazioni tra di essi. Per ogni combinazione, il modello ha fornito valori di interesse legati a:
- tensioni residue superficiali e massime,
- profondità delle zone in compressione,
- rugosità superficiale (parametri Ra e Rc).
Infine, i dati numerici ottenuti sono stati elaborati con la Response Surface Methodology (RSM), che costruisce equazioni matematiche di previsione, e analizzati con l’ANOVA per individuare i fattori più significativi (box 2). L’ottimizzazione multi-obiettivo è stata condotta tramite la funzione di desiderabilità, che permette di bilanciare parametri in conflitto (massima compressione e minima rugosità) e identificare il miglior compromesso operativo.
Analisi preliminare
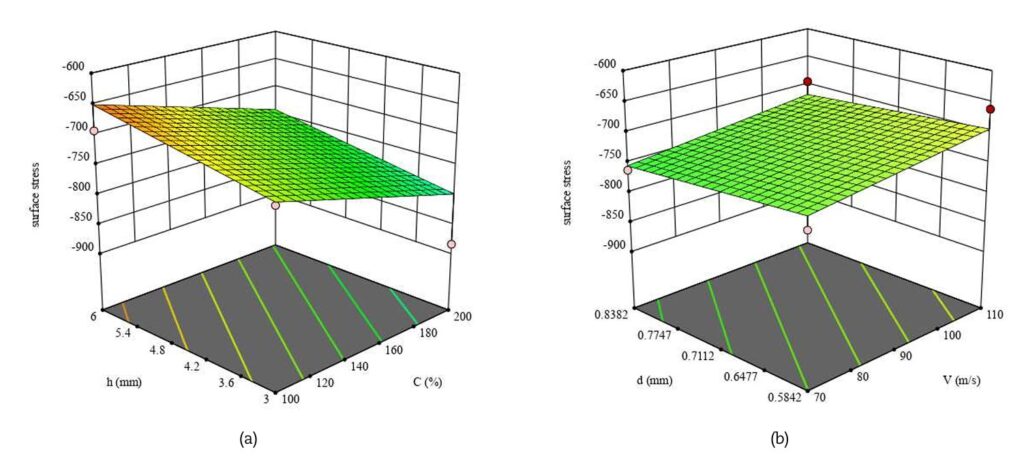
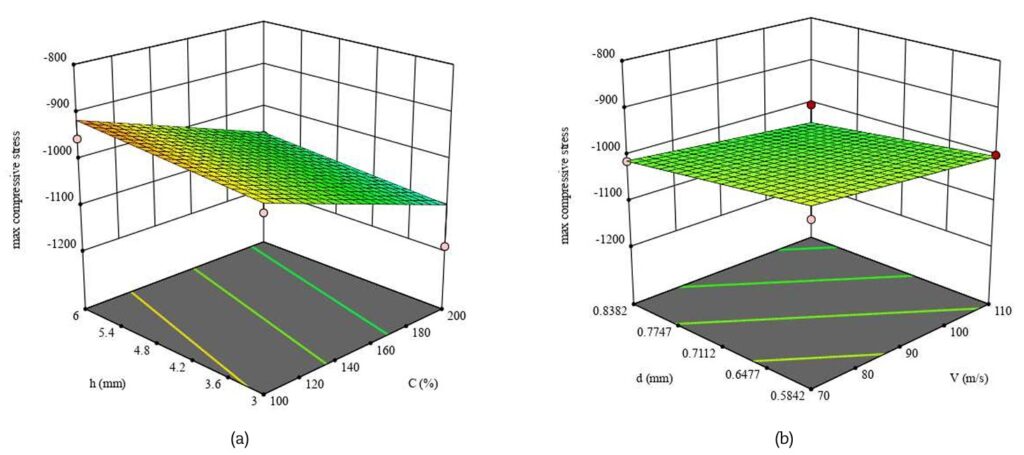
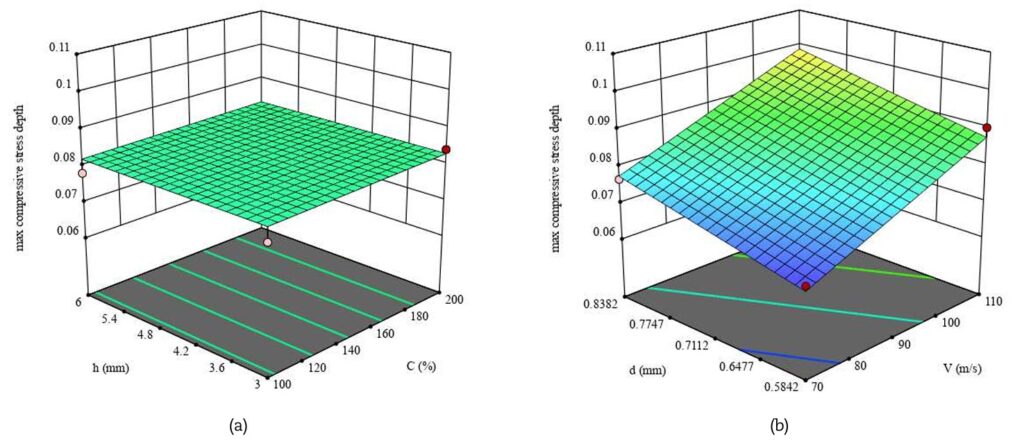
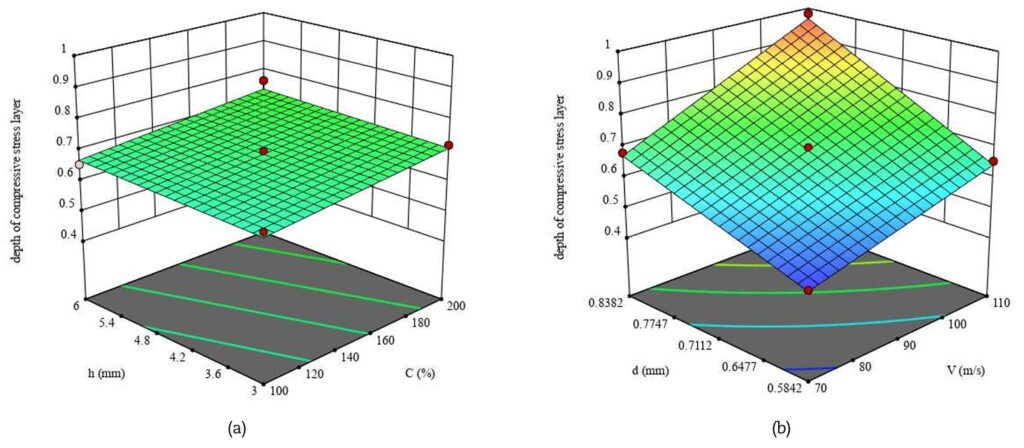
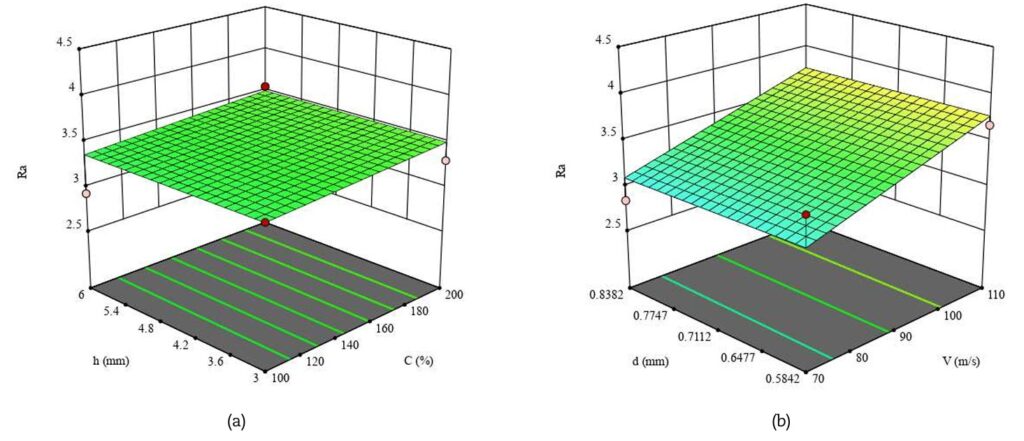
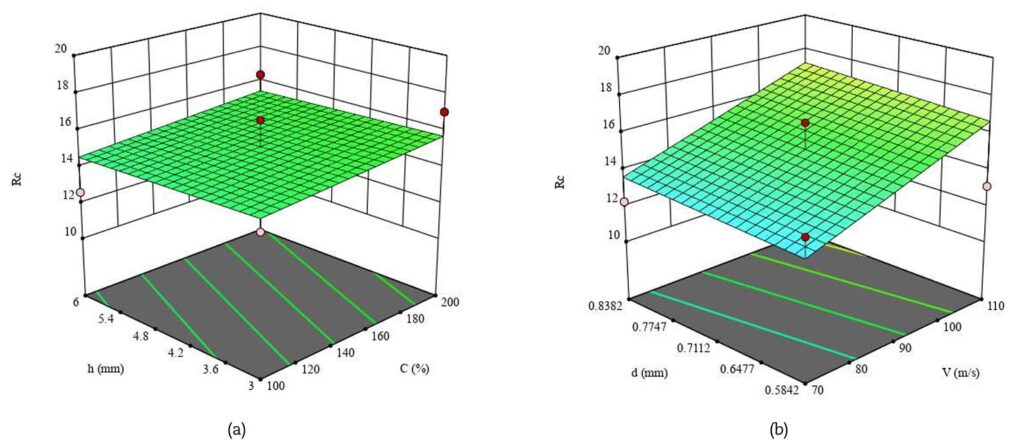
Dall’analisi delle superfici di risposta (RSM) emerge con chiarezza come i diversi parametri di processo influenzino gli esiti della pallinatura. La tensione residua superficiale aumenta al crescere della copertura, mentre tende a ridursi con lo spessore del pezzo, risultando invece poco sensibile alla velocità e al diametro dei pallini (Fig. 3). Diversamente, la tensione residua massima interna è fortemente condizionata dalla copertura e dal diametro dei pallini, mentre la velocità ha un effetto trascurabile (Fig. 4). La profondità a cui si colloca questa massima compressione dipende in modo diretto sia dalla velocità sia dal diametro: incrementi di entrambi i parametri portano la compressione utile a spingersi più in profondità (Fig. 5). Ancora più complessa è la situazione per la profondità complessiva dello strato compresso, governata da tutti i parametri analizzati e in particolare dall’interazione tra velocità e diametro (Fig. 6). Per quanto riguarda le caratteristiche superficiali, sia la rugosità media Ra sia la rugosità Rc (picchi e valli) risultano dominate quasi esclusivamente dalla velocità dei pallini, che ne determina un aumento progressivo (Figg. 7–8).
Risultati e discussione
Le simulazioni numeriche hanno permesso di costruire un quadro chiaro sull’influenza dei parametri di processo. In particolare, in Tabella 1 sono riportati gli effetti della modifica dei principali parametri coinvolti nel processo di pallinatura, quali velocità dei pallini (V), diametro dei pallini (d) e percentuale di copertura (C), rispetto ad un utilizzo su materiali di differente spessore (h). Questi effetti sono valutati in termini di tensione residua superficiale (σRSsurf) e massima (σRSmax), profondità della tensione residua massima (δRSmax) e dello strato compresso (δRSc), rugosità media di picchi e valli principali (Rc) e rugosità media del profilo (Ra), quali valori simulati. Ne emerge come:
1. Tensioni residue superficiali: le tensioni compressive sulla superficie non dipendono in modo significativo né dalla velocità né dal diametro dei pallini, ma sono fortemente influenzate dalla percentuale di copertura e dallo spessore del pezzo. In pratica, aumentando la copertura si incrementa la compressione, mentre uno spessore maggiore tende a ridurne l’intensità superficiale.
2. Tensione residua massima: il valore massimo di compressione raggiunto all’interno del materiale risulta poco sensibile alla velocità, ma dipende in maniera rilevante dalla copertura e dal diametro dei pallini: pallini più grandi e coperture elevate portano a stati tensionali più marcati.
3. Profondità delle tensioni residue: la profondità alla quale si registra la massima compressione cresce con la velocità e con il diametro dei pallini, mentre lo spessore del pezzo ha un ruolo marginale. Diversamente, la profondità complessiva dello strato compresso è influenzata da tutti i parametri: diametro, velocità, copertura e spessore.
4. Rugosità superficiale: la rugosità (sia media, Ra, che di picchi e valli, Rc) è legata quasi esclusivamente alla velocità dei pallini: all’aumentare della velocità, la superficie diventa più irregolare. Ciò significa che incrementare troppo la velocità, pur aumentando la profondità delle tensioni utili, rischia di penalizzare la qualità superficiale.
5. Ottimizzazione complessiva: non è possibile ottimizzare singolarmente ogni parametro senza passare per compromessi sugli altri: ciò che massimizza le tensioni residue, ad esempio, può peggiorare la rugosità, e viceversa. L’uso di una funzione di desiderabilità è sempre necessaria e, questa volta ha permesso di trovare il miglior equilibrio complessivo nel caso di uno stato di compressione profondo e stabile, pur mantenendo al tempo stesso la rugosità entro limiti accettabili. Tali condizioni emergono con: alta copertura (circa 200%), velocità medio-bassa (70–90 m/s), pallini di diametro medio-alto.
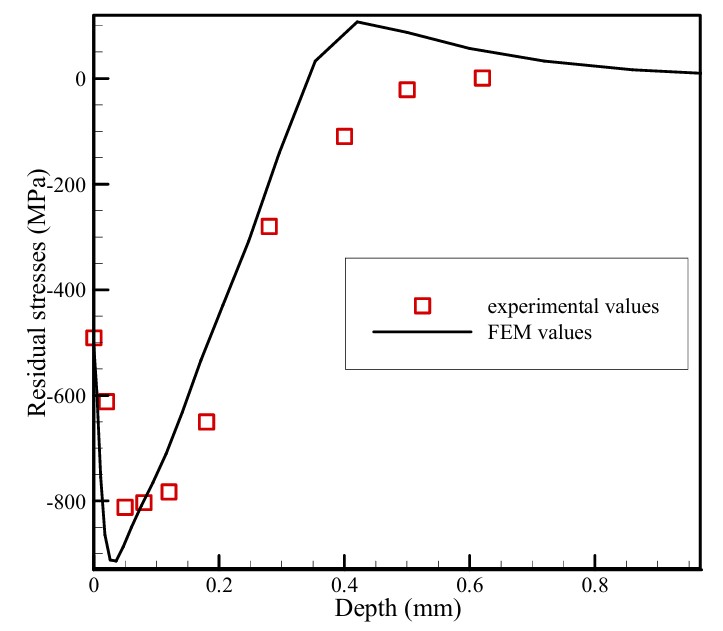
La Tabella 2 riassume i principali risultati dell’analisi ANOVA, mostrando in modo complessivo come i parametri fondamentali del processo di pallinatura (velocità, diametro, copertura, spessore) abbiano una influenza diretta su tensioni residue, profondità degli strati compressi e rugosità superficiale. Per quanto lo studio si sia concentrato sulle sole simulazioni, i risultati del modello sono stati confrontati con misure sperimentali di tensioni residue ottenute tramite diffrazione a raggi X e rimozione elettrolitica di strati. La corrispondenza – verificata alle condizioni (i) Shot S170, (ii) Intensità Almen 14A (equivalente a una velocità di 67,7 m/s), (iii) Copertura 100%, (iv) Angolo di impatto 90°, con coefficiente di attrito μ = 0,2 tra i pallini e la superficie durante il contatto – è risultata soddisfacente (Figura 9), confermando l’affidabilità delle simulazioni numerica e la validità della procedura statistico.
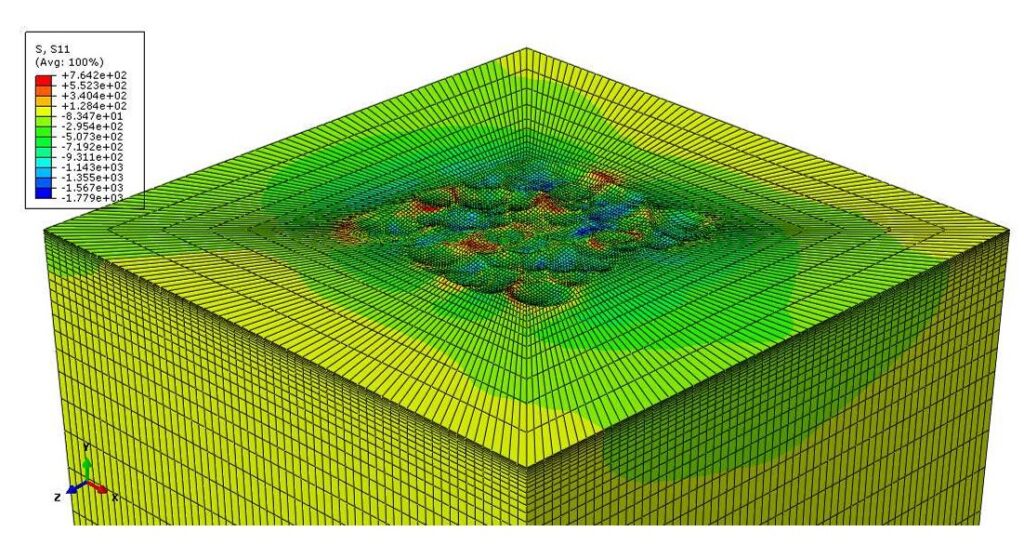
La modellazione del processo di pallinatura si propone così come un utilissimo strumento, che consente di indagare in dettaglio ciò che avviene a diversi livelli del materiale, offrendo una visione più chiara e completa rispetto a quanto si riesce a ottenere sperimentalmente; come mostra la Figura 10, è possibile, ad esempio, visualizzare direttamente non solo la deformazione residua dopo la pallinatura, ma anche la distribuzione delle tensioni sulla superficie trattata, rendendo più semplice e accurata la comprensione dei meccanismi in gioco.
Modelli matematici semplificati
Da questa analisi sono stati infine ricavati modelli matematici semplificati che descrivono come i parametri di processo influenzano le principali risposte della pallinatura. Ogni modello è espresso come funzione lineare (o quasi-lineare) dei diversi fattori considerati e permette di individuare con immediatezza quali parametri hanno un peso reale sul fenomeno e quali risultano invece trascurabili. In particolare, emerge che:
- La copertura (C) risulta determinante per le tensioni residue superficiali e massime, confermando che una percentuale elevata garantisce un incremento della compressione utile.
- Il diametro dei pallini (d) incide sia sulla tensione residua massima che sulla profondità delle compressioni, mostrando che pallini più grandi trasferiscono energia più in profondità.
- La velocità di impatto (V) ha effetto minimo sulle tensioni superficiali, ma controlla la profondità della compressione e domina la rugosità, che cresce linearmente con l’aumento della velocità.
- Lo spessore del materiale (h) influisce sulla distribuzione delle tensioni residue, riducendo la compressione superficiale e contribuendo alla profondità complessiva dello strato compresso.
- Alcuni effetti combinati quali l’interazione tra velocità e diametro dei pallini (V×d) risultano spesso particolarmente significativi, molto più dei parametri singoli, per spiegare fenomeni quali la profondità complessiva della zona compressa.
In Tabella 3 sono riepilogati i modelli matematici associati a ciascuna risposta e i parametri di processo che ne influenzano maggiormente l’andamento.
Conclusioni
Lo studio ha dimostrato che la pallinatura può essere efficacemente analizzata e ottimizzata attraverso la combinazione di simulazioni numeriche FEM e metodi statistici (RSM e ANOVA). Questo approccio consente di ridurre la dipendenza da prove sperimentali estese, fornendo modelli predittivi affidabili per la scelta dei parametri di processo. Viene evidenziato che:
- la copertura è il parametro chiave per incrementare le tensioni residue superficiali e massime.
- il diametro dei pallini influenza sia l’intensità sia la profondità delle compressioni.
- la velocità di impatto determina la profondità della zona compressa, ma incide negativamente sulla rugosità, che cresce linearmente.
- lo spessore del pezzo non è neutro: modifica la distribuzione delle tensioni e contribuisce alla profondità dello strato compresso.
- l’interazione velocità × diametro ha un effetto rilevante sulla profondità dello strato in compressione.
L’ottimizzazione multi-obiettivo ha individuato come condizioni ottimali una copertura elevata (≈200%) e una velocità medio-bassa (70–90 m/s), con pallini di diametro medio-alto. Questo compromesso garantisce un buono stato di compressione interna riducendo al minimo l’aumento della rugosità superficiale.
Approfondimenti
- Hassanzadeh M., Moussavi Torshizi S.E. (2022). Multi-objective Optimization of Shot-peening Parameters using Design of Experiments and Finite Element Simulation: A Statistical Model. Journal of Applied and Computational Mechanics, 8(3), 838–852.
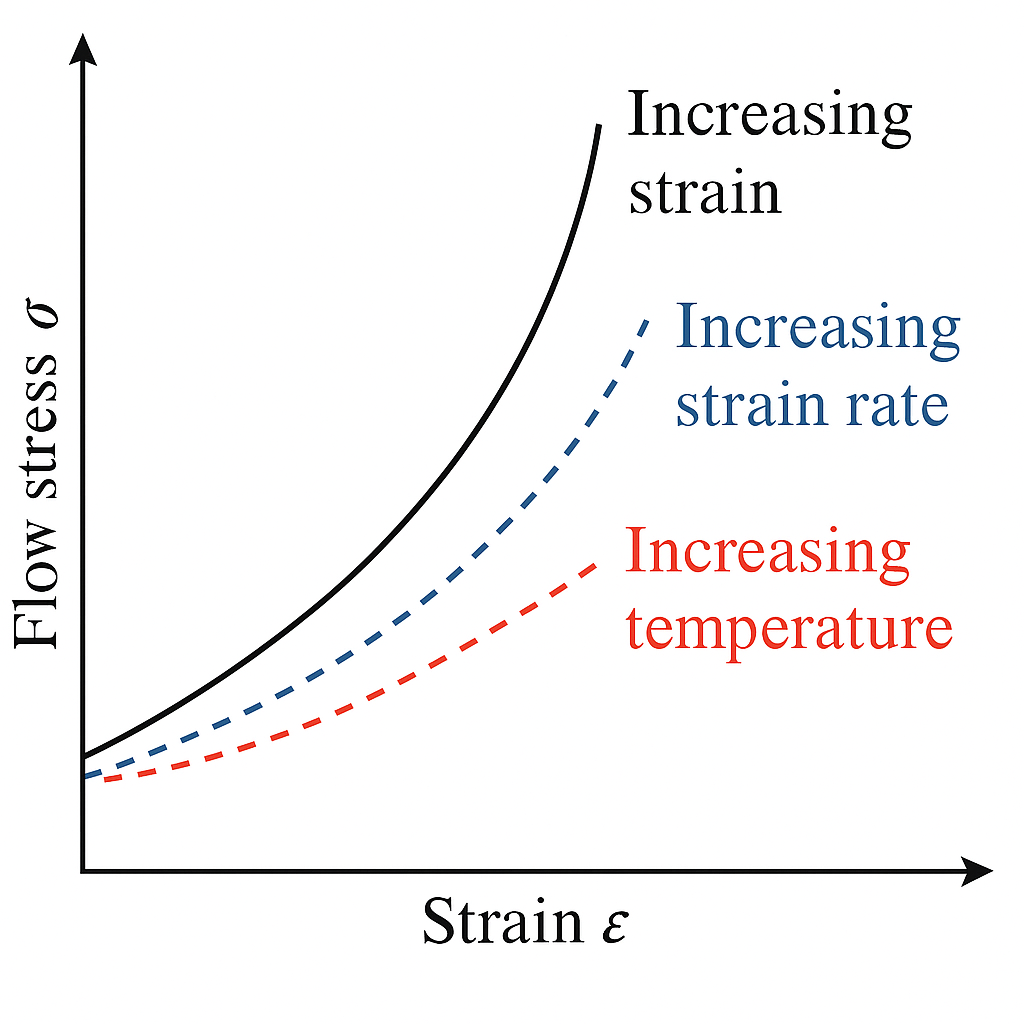
L’equazione base del modello esprime la tensione di flusso σ, ossia il valore della tensione effettiva che il materiale deve sopportare per continuare a deformarsi plasticamente nelle condizioni date, come prodotto di tre termini:
1. Componente di incrudimento: σ = A + B εⁿ
dove ε è la deformazione plastica equivalente, A rappresenta il limite di snervamento iniziale, B il coefficiente di incrudimento e n l’esponente di incrudimento. Questo termine descrive l’aumento di resistenza del materiale al crescere della deformazione plastica.
2. Componente di sensibilità alla velocità di deformazione: (1 + C ln(ε̇ / ε̇₀))
dove ε̇ è la velocità di deformazione, ε̇₀ un valore di riferimento e C un coefficiente che quantifica la sensibilità del materiale alla velocità di carico. In pratica, a deformazioni più rapide corrisponde una resistenza più elevata.
3. Componente di softening termico: (1 − (T − T₀) / (Tₘ − T₀))ᵐ
dove T è la temperatura istantanea, T₀ la temperatura ambiente, Tₘ quella di fusione e m un coefficiente che descrive l’ammorbidimento a caldo. All’aumentare della temperatura, la resistenza del materiale cala progressivamente.
La resistenza del materiale cresce con l’aumento della deformazione plastica (incrudimento) e con la velocità di deformazione, mentre diminuisce al crescere della temperatura per effetto di softening termico (Figura 11). Combinando questi tre termini, il modello Johnson–Cook consente di catturare in modo compatto l’effetto simultaneo di deformazione, velocità e temperatura. Per questo motivo è largamente adottato nelle simulazioni FEM di processi dinamici, come la pallinatura, in cui il materiale è sottoposto a urti ripetuti, deformazioni localizzate e condizioni di elevata velocità.
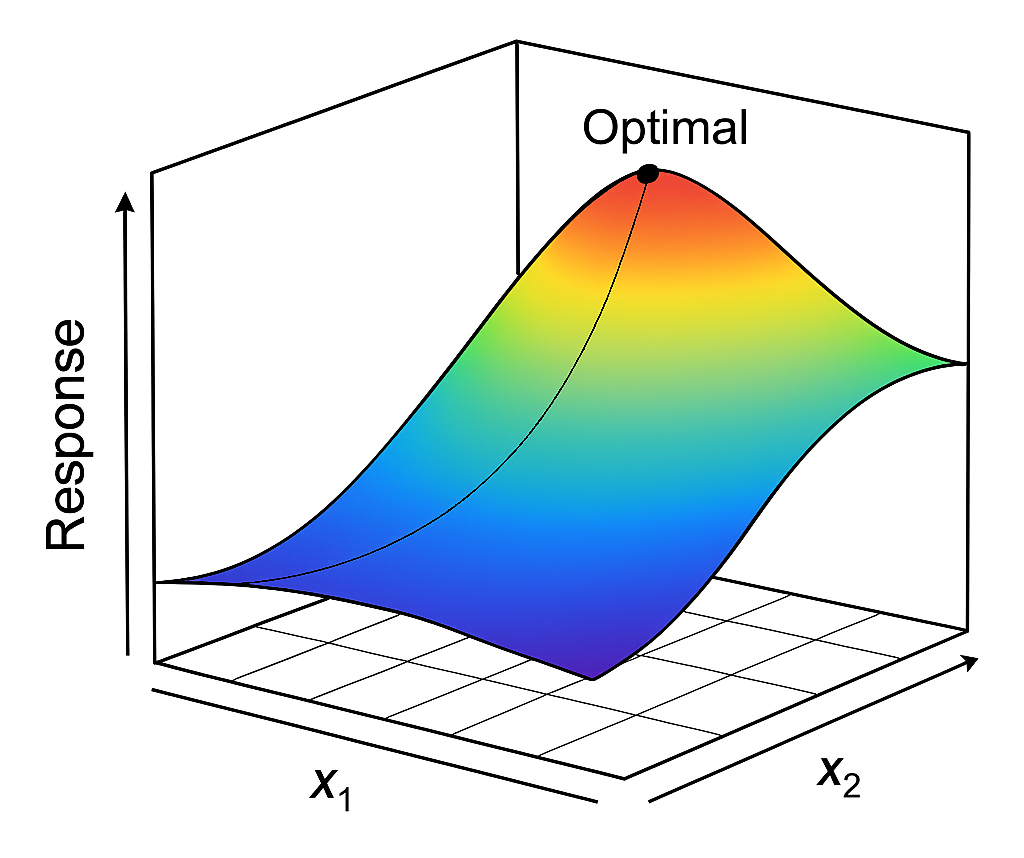
Il modello più utilizzato è una funzione polinomiale di secondo grado, che permette di rappresentare sia gli effetti lineari dei fattori, sia le loro interazioni, sia eventuali curvature nelle risposte (Figura 12). A partire dai dati raccolti con un piano sperimentale opportuno, di Design of Experiment (DoE), si applica una regressione statistica per stimare i coefficienti del modello.
Una volta costruita la “superficie di risposta”, diventa possibile:
• Visualizzare graficamente come i parametri influenzano le variabili di output (es. tensioni residue, rugosità);
• Individuare zone ottimali di lavoro, bilanciando parametri in conflitto;
• Ridurre il numero di prove reali, perché le simulazioni o gli esperimenti sono selezionati in modo mirato;
• Valutare le interazioni tra fattori, che spesso sfuggono se analizzati singolarmente.
In contesti industriali, la RSM è uno strumento molto utile per tradurre i risultati di simulazioni numeriche o test sperimentali in linee guida pratiche: permette di capire non solo quali parametri contano di più, ma anche come impostarli per ottenere il miglior compromesso tra prestazioni, costi e qualità del prodotto.
Il principio è semplice: la variabilità complessiva dei dati viene scomposta in due parti:
• la quota spiegata dal modello, cioè attribuibile ai fattori considerati (es. velocità, diametro, copertura, spessore nel caso della pallinatura);
• la quota residua, dovuta a errori o variazioni non spiegate.
Per ciascun fattore l’ANOVA calcola:
• la somma dei quadrati (SS), che misura la variabilità spiegata;
• i gradi di libertà (gdl), legati al numero di livelli del fattore;
• il quadrato medio (MS), rapporto tra SS e gdl;
• il valore F, che confronta la variabilità spiegata da quel fattore con la variabilità residua;
• il p-value, che indica la probabilità che l’effetto osservato sia dovuto al caso.
Nella pratica industriale, un p-value < 0,05 segnala che il fattore è statisticamente significativo, ossia incide realmente sul processo. Se il p-value è più alto, il fattore può essere trascurato nelle decisioni operative.
Applicata a processi complessi come la pallinatura, l’ANOVA diventa uno strumento decisionale: permette di stabilire rapidamente su quali parametri concentrare il controllo e l’ottimizzazione, evitando sprechi di tempo e risorse su variabili poco influenti.

