Assi e alberi: progetto, dimensionamento e verifica statica

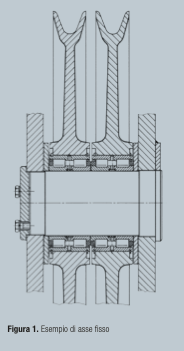
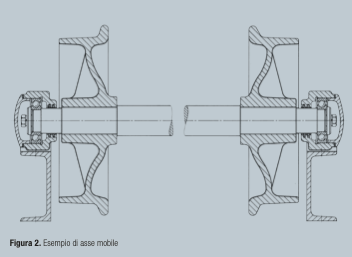
Gli assi possono essere fissi o rotanti e si distinguono dagli alberi per il fatto che non trasmettono momento torcente: la loro funzione è quella di supportare ruote, carrucole,  rulli avvolgitori, pulegge per cinghie e catene e simili. Sono sollecitati a flessione, che può essere statica o di fatica con cicli diversi in relazione allo specifico caso.

Gli alberi sono invece sempre rotanti e trasmettono momento torcente, come avviene nei motori, nelle turbine, nei cambi e in moltissime altre applicazioni: sono pertanto sollecitati a torsione o a torsione e flessione. Il momento torcente viene introdotto nell’albero mediante giunti o innesti, oppure mediante organi calettati su di esso, quali le ruote dentate delle trasmissioni ad ingranaggi o le ruote dentate per catene o le pulegge per cinghie.

Gli alberi possono essere classificati secondo svariati criteri: ad esempio, secondo la sezione, possiamo distinguere tra alberi tondi o profilati, o tra alberi pieni e cavi. Possiamo poi distinguere i generici alberi ad asse rettilineo da quelli speciali, come gli alberi a gomito, gli alberi a camme e quelli cardanici. Oppure possiamo differenziare quelli rigidi da quelli flessibili. Anche la lunghezza può costituire elemento di classificazione, in alberi lunghi e alberi corti, perché al suo variare si modifica il rapporto tra le verifiche che si eseguono sull’albero e pertanto cambia la condizione più limitativa, così come risulta influenzata la scelta del materiale.

Progetto

Una volta specificate le funzioni che l’albero deve assolvere, si devono identificare le forze e i momenti al quale l’albero è sottoposto, a partire dal momento torcente, la cui entità discende dalla potenza da trasmettere e dalla velocità di rotazione. La valutazione del momento flettente richiede invece la conoscenza delle lunghezze e della posizione dei supporti, che nelle fasi preliminari possono essere ancora indeterminati, ma riguardo ai quali si devono fare delle ipotesi iniziali per poter procedere.

La scelta del materiale è in genere influenzata da numerosi fattori, ma vi sono alcuni elementi fondamentali dei quali si deve tenere conto. Innanzitutto bisogna differenziare il caso degli alberi nei quali le forze e i momenti sono applicati con azioni dirette di contatto con rotolamento e strisciamento, per i quali si devono utilizzare materiali in grado di resistere anche a fatica da contatto e/o ad usura, caratterizzati quindi da elevate durezze superficiali, come quelle ottenibili con acciai da cementazione e nitrurazione. Tale indicazione vale anche quando l’albero porta “di pezzo” un organo sollecitato a fatica superficiale o a usura, come nel caso di un pignone, la cui presenza può ad esempio indirizzare verso l’uso di un materiale cementato. Diversamente, quando le sollecitazioni sono trasmesse all’albero mediante elementi calettati su di esso senza moti relativi, come nel caso di giunti, innesti, anelli di cuscinetti, ruote e pulegge varie, si opta tipicamente per gli acciai da bonifica. Come anticipato, la lunghezza può influenzare la scelta del materiale: negli alberi lunghi, a causa della loro flessibilità, la verifica a deformabilità può divenire la più restrittiva e in questo caso, tenuto conto che tutti gli acciai hanno grosso modo lo stesso modulo elastico, non si ha nessun beneficio aumentando la resistenza del materiale; viceversa, negli alberi corti, per i quali la resistenza a fatica risulta generalmente il fattore limitante, si ha ovviamente vantaggio se si scegli un acciaio ad alta resistenza.

Non deve essere trascurata anche la definizione dei vincoli, nella maggioranza dei casi realizzati medianti cuscinetti a rotolamento. La “regola” è costituita dall’utilizzo di una condizione di vincolo isostatica, ottenuta mediante un cuscinetto libero assialmente (floating, in inglese) e uno bloccato (locating), che spesso vengono indicati anche mediante i termini di carrello e cerniera.

Tuttavia nella pratica, tenuto conto che vi sono spesso requisiti particolari da soddisfare, in termini di rigidezze o di limitazione dei giochi, sono possibili svariati altri schemi di vincolo, come ad esempio quelli basati sull’utilizzo di cuscinetti obliqui montati in opposizione.

Una volta configurato, le principali verifiche alle quali si dovrà sottoporre l’albero sono le seguenti:

• verifica di resistenza statica;
• verifica di resistenza a fatica;
• verifica alla deformabilità (limitazione di frecce e rotazioni);
• verifica alle velocità critiche flessionali e torsionali;
• verifica a fatica da contatto e/o a usura dove appropriata.

Dimensionamento

Le suddette verifiche di dettaglio sono possibili solamente quando l’albero è stato pre-dimensionato, cioè quando si ha una configurazione sufficientemente definita sulla quale eseguirle. Come già anticipato, il rapporto tra la restrittività delle diverse verifiche è influenzato da diversi fattori e pertanto, nella fase di dimensionamento iniziale, non è possibile tenere conto di tutte quante:  si procede con una determinazione di massima delle dimensioni, basata sulla verifica di resistenza agli sforzi presenti, calcolati in modo approssimativo e confrontati con limiti del materiale valutati con ampi margini.

Al fine di calcolare gli sforzi agenti nell’albero, dopo averne definito la lunghezza, la distanza tra i supporti e la posizione degli elementi su di esso calettati, si è soliti schematizzarlo mediante un modello a trave, con il quale si possono calcolare le reazioni vincolari, trasversali e assiali, e i diagrammi delle azioni interne, in particolare taglio, azione assiale, momento flettente e torcente.

In generale, tenuto conto che l’albero è sottoposto a forze agenti in piani diversi, è necessario realizzare un modello spaziale, il quale richiede che lo studio della trave venga effettuato su due piani tra di loro perpendicolari: ciò produrrà reazioni vincolari e diagrammi delle azioni interne per ciascun piano, che dovranno poi essere composte vettorialmente, sezione per sezione. Solo in alcuni casi particolari, è possibile ricondurre lo studio ad un singolo piano.

Non vengono qui descritti i singoli passi della procedura mediante la quale si modella la trave e la si risolve, ma si riporta un esempio tratto da [1], che si riferisce al caso di un albero intermedio di un riduttore ad ingranaggi cilindrici a denti diritti, che viene qui mostrato graficamente a titolo illustrativo in figura 3, senza entrare nel dettaglio della definizione dei valori numerici.

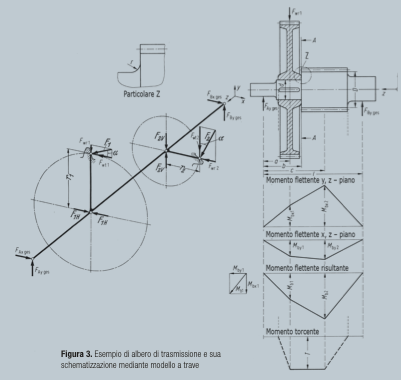
Una volta completati i calcoli sullo schema a trave, sono noti i valori massimi del momento flettente e del momento torcente, che potranno essere utilizzati per dimensionare l’asse o l’albero in oggetto.

Nel caso degli assi, sottoposti a sola flessione, il dimensionamento viene effettuato limitando lo sforzo di flessione nella sezione in cui è massimo. Nel caso più frequente di albero a sezione circolare piena, il massimo sforzo di flessione è dato dalla relazione:

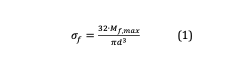
nella quale compaiono, con evidente significato dei simboli, il momento flettente e il diametro.

Risolvendo  la  disequazione che limita detto sforzo al valore ammissibile, si ottiene per il diametro dell’albero la seguente condizione:

Il valore così calcolato costituisce un diametro medio di riferimento, attorno al quale verrà plasmata l’effettiva geometria dell’albero, che non potrà prescindere da spallamenti e  variazioni di diametro lungo il suo sviluppo, necessari al calettamento degli organi di macchine, il cui dettaglio dovrà essere definito successivamente.

La sollecitazione ammissibile da utilizzare nella (2) dovrà essere determinata con ampio margine, tenuto conto che in questa fase non si entra nel merito delle specifiche condizioni di sollecitazione, quali le caratteristiche del ciclo e la presenza di intaglio e degli altri effetti, nel caso della fatica. Un’indicazione è quella di utilizzare, per lo sforzo ammissibile di flessione, un sesto del carico unitario di rottura a trazione, secondo la seguente formula:

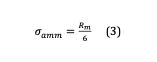
Vale la pena di sottolineare che questo diametro, scelto con una procedura alquanto approssimativa, costituisce solamente un valore iniziale per poter eseguire i successivi calcoli, grazie ai quali si potrà pervenire ad una definizione accurata e particolareggiata del diametro dell’albero nelle varie sezioni, a prescindere dal fatto che il valore di partenza fosse già una stima sufficientemente accurata. In altri termini, l’ampio margine introdotto in questa fase, non pregiudica il risultato finale.

Nel caso di albero sottoposto a torsione, si dovrà limitare il massimo sforzo di scorrimento determinato dal momento torcente, utilizzando le formule seguenti:

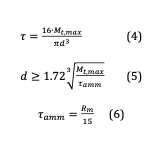
Nel caso di torsione e flessione combinate, si può calcolare un momento flettente equivalente e poi procedere come nel caso della flessione:

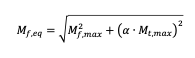
con:

α²= 0.25 nel caso di flessione rotante con torsione pulsante o costante;

α²= 0.75 nel caso di flessione rotante con torsione alternata.

Una volta stabilito il diametro come sopra indicato, si potrà procedere alla definizione della geometria dettagliata dell’albero, necessaria per l’esecuzione delle successive verifiche.

Verifica di resistenza statica

Per la verifica di resistenza statica, si indica qui il procedimento per il caso più generale di presenza di flessione e torsione combinate. La verifica statica ha la finalità di assicurare che, nelle condizioni di massima sollecitazione alla quale potrà essere sottoposto l’albero nella sua vita, non si abbia il cedimento statico dello stesso. Non verrà quindi eseguita in condizioni di carico nominale, ma ricercando la condizione più gravosa, dovuta ad esempio alla coppia di spunto all’avviamento, o comunque considerando ogni possibile sovraccarico derivante da altre cause.

La verifica statica viene generalmente eseguita rispetto alle condizioni di “carico ultimo” sopportabile dalla sezione dell’albero che, se in acciaio, beneficia della duttilità del materiale grazie alla quale, a differenza dei materiali fragili, una volta raggiunto il limite elastico nel punto più sollecitato si ha la ridistribuzione degli sforzi, senza che si produca la rottura del componente. Inoltre, nel caso della flessione e della torsione, si potrebbe invocare l’ulteriore beneficio derivante dal coefficiente di collaborazione, che però nel seguito sarà ignorato.

In queste condizioni, dal punto di vista pratico, si potrà eseguire la verifica statica senza tenere conto dell’effetto del coefficiente d’intaglio.

Utilizzando i criteri di resistenza di Von Mises e di Guest-Tresa, si potrà scrivere per il coefficiente di sicurezza a carico ultimo (o plasticizzazione totale) rispettivamente:

Nelle quali compaiono appunto gli sforzi nominali, cioè non incrementati per effetto dell’intaglio.

Tenuto conto che la deformazione plastica dell’albero in corrispondenza del carico ultimo può, in talune applicazioni, non essere ammissibile, si può, in questi casi, introdurre una limitazione assai più restrittiva, consistente nel prevenire che anche soltanto localmente si ecceda il limite elastico del materiale (inizio plasticizzazione): dal punto di vista pratico, ciò significa riscrivere le condizioni di verifica, introducendovi gli sforzi massimi, pari a quelli nominali moltiplicati per il rispettivo coefficiente d’intaglio:

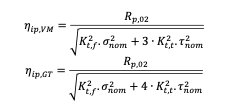
Per approfondimenti, si rimanda a [1]. Le ulteriori verifiche saranno trattate nella seconda parte.

Per una trattazione organica dell’argomento si veda il “Manuale degli Organi delle Macchine”