Le misurazioni tramite diffrazione dei raggi x, normalmente indicate con il loro acronimo inglese XRD (X Ray Diffraction) sono ormai una tecnologia ampiamente utilizzata in ambito meccanico per lo studio e la caratterizzazione dei materiali a struttura cristallina (come i metalli), grazie soprattutto alla loro caratteristica di essere completamente non distruttive e di poter fornire informazioni puntuali. Illustreremo come l’analisi della “larghezza” di un picco di diffrazione possa fornire indicazioni sulla presenza di micro deformazioni plastiche, e come tale informazione possa essere utilizzata per verificare l’efficacia di trattamenti termici di distensione.
di Francesco Chichi
Come anticipato nell’introduzione, le misurazioni basate sul fenomeno della diffrazione dei raggi X possono essere utilizzate unicamente su materiali cristallini, ossia materiali i cui atomi sono organizzati secondo una struttura geometricamente ordinata e simmetrica, basata sulla ripetizione tridimensionale di una struttura-base che prende il nome di cella elementare (fig. 1)
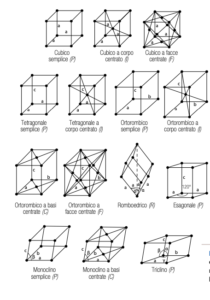
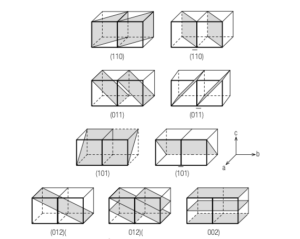
Tale struttura organizzata costituisce il reticolo cristallino, nel quale è sempre possibile individuare diversi piani reticolari (fig. 2).
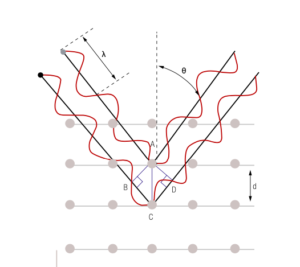
Andando a colpire il reticolo cristallino con un fascio di raggi X di opportuna lunghezza d’onda, tale fascio viene diffratto seguendo la cosiddetta legge di Braggs, per la quale la quale la radiazione diffratta da piani reticolari adiacenti ha interferenza costruttiva solo quando la distanza interplanare “d” risulta pari a (fig. 3)
Essendo:
l= lunghezza d’onda della radiazione incidente
Q = angolo relativo tra la radiazione incidente e il piano reticolare
n= numero intero, solitamente posto pari ad 1
possiamo pertanto dire che ad ognuno dei piani reticolari presenti in un reticolo cristallino è associabile un “angolo di diffrazione”, ossia un valore angolare per cui il fascio diffratto risulta coerente e quindi rilevabile in intensità.
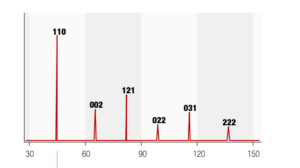
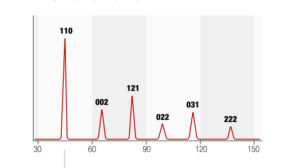
A titolo esemplificativo nella figura 4 è rappresentato uno spettro di diffrazione ideale prodotto da un campione di acciaio illuminato da un fascio di raggi X prodotto da un anodo Cu Ka con lunghezza d’onda l = 1,5402 Angstrom, dove i piani reticolari associati ad ogni angolo di diffrazione sono identificati mediante il relativo indice cristallografico di Miller.
Nella realtà la forma dei picchi di diffrazione non è così “pulita” come quella di figura 4, e questo dipende dal fatto che nella realtà non esistono strutture cristalline perfette come quelle che abbiamo descritto fino ad ora.
Dal cristallo al cristallite
Questo articolo si è aperto con la descrizione della struttura cristallina, descritta come una ripetizione tridimensionale ordinata di un “modulo base” costituito dalla cella elementare.
Nella realtà una tale ripetizione tridimensionale “all’infinito” è tutt’altro che la regola, costituendo anzi una rarissima eccezione , ottenibile solo con notevoli sforzi in condizioni di laboratorio: nella totalità dei materiali ingegneristici difetti reticolari, imperfezioni, fenomeni di soluzione solida e un infinità di altri elementi di disturbo fanno si che le porzioni di materiale aventi effettivamente una struttura cristallina omogenea abbiano dimensioni veramente ridotte, indicativamente da 10 a 50 mm: tale porzione di materiale caratterizzata da una struttura cristallina regolare ed omogenea costituisce un cristallite.
Nella figura 5 sono riportati il caso di una struttura cristallina ideale e una reale, dove una singola distorsione reticolare comporta la comparsa di 4 diversi sistemi reticolari coerenti, costituenti ciascuno un cristallite: in pratica il cristallite può quindi essere considerato come la porzione di materiale assimilabile ad un monocristallo.
La presenza di questi sistemi con orientamento reticolare leggermente deviato rispetto alla condizione ideale fa si che la diffrazione non sia più concentrata in corrispondenza di un unico esatto valore angolare, ma risulti dispersa secondo una gaussiana intorno a tale valore “ideale”: nella figura 6 è riportata la forma reale dello spettro di diffrazione ideale riportato in figura 5, dove le linee di diffrazione scompaiono per lasciare spazio a curve di larghezza finita.
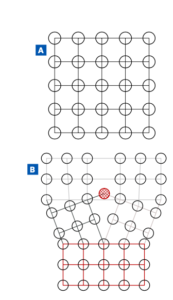
5b: condizione reale: la presenza di una singola irregolarità nel reticolo cristallino comporta la comparsa di 4 diversi sistemi di piani reticolari coerenti rispetto a loro stessi (evidenziati nei diversi colori), corrispondente ciascuno ad un diverso cristallite
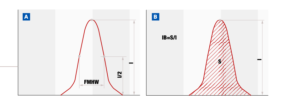
La “dispersione” della curva spettrale rispetto al valore angolare teorico è solitamente espressa mediante i parametri FWHM (Full Width at Half Maximum) o IB (integral breadth) , dove con FWHM si intende la larghezza della curva al 50% dell’altezza del picco , mentre con IB si intende la superficie sottesa alla curva normalizzata rispetto al valore di picco (fig. 7): entrambi questi parametri finiscono quindi per essere indicatori di quella che è la densità delle dislocazioni nel volume di materiale irradiato dal fascio di raggi X (solitamente uno spot di diametro 1mm e profondità di penetrazione di qualche decina di micron), e di conseguenza fornire la base per esprimere una sorta di “dimensione media” dei cristalliti nel suddetto volume.
Significato metallurgico delle dislocazioni
Come abbiamo appena detto, da un’analisi quantitativa del profilo della curva sottesa ad un picco di diffrazione è possibile ricavare informazioni sulla densità di dislocazioni presenti nel materiale, e di conseguenza avere una quantificazione della omogeneità della struttura cristallina del materiale.
Da un punto di vista metallurgico, le dislocazioni sono comunque sempre presenti nei materiali ingegneristici, ma soprattutto si vengono a creare a seguito di deformazioni plastiche: possiamo anzi dire che proprio la coalescenza di vacanze e impurità in fronti di dislocazione è il meccanismo che permette lo scorrimento dei piani cristallini attraverso cui la deformazione plastica assume il suo aspetto macroscopico.
Tali deformazioni plastiche possono essere un effetto diretto (come nelle operazioni di forgiatura) o collaterale (come nelle operazioni di lavorazione per asportazione di truciolo) delle lavorazioni, ma possono anche essere l’effetto di trattamenti termici come la tempra, tali da impedire una naturale orientazione in fase di raffreddamento dei piani reticolari.
Ecco cosi che la misurazione delle dimensioni del cristallite diventa un informazione correlata allo stato di rilassamento del materiale, e il confronto comparativo delle dimensioni del cristallite prima e dopo un trattamento termico diventa un elementi di verifica e controllo dell’efficacia del trattamento termico, e analogamente la diminuzione o l’aumento delle dimensioni del cristallite a seguito di una lavorazione diventa un indice dell’eventuale danneggiamento a livello microscopico indotto dalla lavorazione stessa.
A titolo esemplificativo si può citare il caso di estrusi in lega 6063 – T6, considerati prima nello stato lasciato dalla estrusione, poi sottoposti a lavorazione di macchina ed infine sottoposti ad un processo di distensione alla temperatura di 300 °C e successivo raffreddamento in aria ferma.
Nello stato in cui si trova al termine del processo di estrusione, la dimensione media del cristallite in superficie risulta pari a 80 nm: procedendo ad una opportuna asportazione elettrochimica è stato possibile ricostruire l’andamento delle dimensioni medie del cristallite fino alla profondità di 250 micron (0,25mm) , con un andamento della dimensione media progressivamente crescente fino a stabilizzarsi intorno al valore di 120 nm; contestualmente, la determinazione delle tensioni residue, effettuata sempre per via diffrattometrica, vede un andamento come da tabella 1, i cui risultati sono riportati in forma grafica nelle figure 8 e 9.
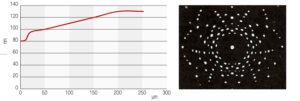
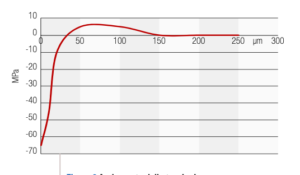
Tabella 1
| profondità | dimensioni cristallite (nm) | tensioni residue (Mpa) |
| 0 | 80 | -65 |
| 10 | 82 | -45 |
| 20 | 95 | -10 |
| 50 | 100 | 5 |
| 100 | 110 | 5 |
| 150 | 120 | 0 |
| 200 | 130 | 0 |
| 250 | 130 | 0 |
Sottoponendo tali campioni ad una successiva lavorazione di asportazione di truciolo per la spianatura della superficie, l’andamento in funzione della profondità delle dimensioni medie del cristallite e delle tensioni residue è come da tabella 2, con gli andamenti grafici riportati nelle figure 11 e 12.
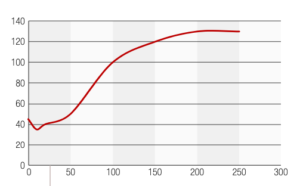
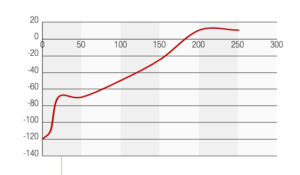
Tabella 2
| profondità | cristallite | tensioni residue |
| 0 | 45 | -120 |
| 10 | 35 | -110 |
| 20 | 40 | -70 |
| 50 | 50 | -70 |
| 100 | 100 | -50 |
| 150 | 120 | -25 |
| 200 | 130 | 10 |
| 250 | 130 | 10 |
Per concludere, l’andamento in funzione della profondità delle dimensioni medie del cristallite e delle tensioni residue successivamente al trattamento termico di distensione è come da tabella 3 , con gli andamenti grafici riportati nelle figure 13 e 14.
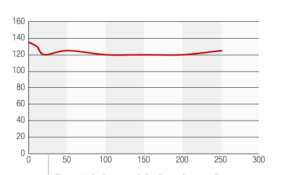
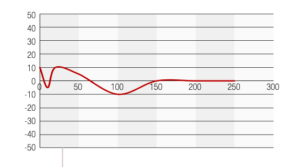
Tabella 3
| profondità | cristallite | tensioni residue |
| 0 | 135 | 10 |
| 10 | 130 | -5 |
| 20 | 120 | 10 |
| 50 | 125 | 5 |
| 100 | 120 | -10 |
| 150 | 120 | 0 |
| 200 | 120 | 0 |
| 250 | 125 | 0 |
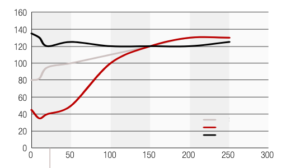
Analisi dei risultati
Quali siano gli effetti del processo di estrusione, delle lavorazioni di macchina e dei trattamenti termici di distensione sullo stato di deformazione plastica (o equivalentemente sulla densità delle dislocazioni), e metallurgicamente ben noto, cosi come quali siano le distribuzioni di tensioni residue che si possono attendere.
Il trattamento termico di distensione riporta la dimensione media del cristallite al suo valore “a cuore” di 120 – 130 nm, con fenomeni di ingrossamento del grano in superficie.
La relazione tra dimensione del cristallite e fenomeni di plasticizzazione è per altro confermata anche dalle determinazione delle tensioni residue, che nel caso del trattamento termico risultano annullate (con la dimensione del cristallite ai suoi valori massimi) mentre nel caso di estrusione e lavorazione meccanica sono presenti tensioni residue di compressione per una profondità leggermente superiore a quella per cui si riscontrano frazionamenti del cristallite: effetto anche questo atteso, in quanto lo stato tensionale indotto dalla deformazione plastica è ovviamente esteso anche alle adiacenti porzioni di materiale ancora in regime elastico.


