L’uso dei cuscinetti a gas è stato recentemente esteso a nuove applicazioni. Viene qui descritta l’importanza di alcuni aspetti come l’interazione fluido-struttura e la presenza di possibili errori di produzione per ottenere dei modelli numerici quanto più possibile fedeli ai prototipi reali
Federico Colombo, Luigi Lentini, Terenziano Raparelli, Andrea Trivella
Grazie alla loro affidabilità, ripetibilità e attrito praticamente nullo, i cuscinetti a gas vengono largamente utilizzati in applicazioni di tipo metrologico o manifatturiero come ad esempio machine di misura, guide lineari, tavole rotanti e macchine per fresature a specchio.
Inoltre, grazie alla loro eco-compatibilità e pulizia l’utilizzo di questa tipologia di supporti si sta ampiamente diffondendo anche in settori come la produzione di semiconduttori, il test di schede elettroniche e nelle turbomacchine miniaturizzate.
Questa maggiore diffusione sta anche portando a richieste sempre più stringenti che non si limitano più solo al garantire il soddisfacimento di alcuni requisiti minimi ma all’assicurare con una certa accuratezza determinate caratteristiche statiche o dinamiche.
Fattori quali errori di produzione e interazione tra più fisiche differenti, come dilatazioni termiche e deformazioni elastiche, possono portare a ottenere, a seconda dei casi, anche variazioni del 10-15% rispetto alle performance attese.
Infatti, solamente considerando gli errori legati al processo produttivo di un cuscinetto è possibile incorrere in macro o micro-errori geometrici come errori di planarità o circolarità delle superfici e/o a imperfezioni relative alla realizzazione dei fori di alimentazione del cuscinetto: cianfrinature, raggi di raccordo o piccole tasche create a seguito dell’inserimento di inserti.
I primi studi riguardo gli effetti di questa tipologia di errori sulle performance di cuscinetti a gas risalgono agli inizi degli anni Ottanta quando la potenza dei modelli numerici e dei calcolatori aveva raggiunto dei livelli di accuratezza sufficiente per poter effettuare questo tipo di valutazioni.
Ad esempio, in questi primi lavori K.J. Stout e E.G. Pink [1,2], dopo aver osservato che in alcuni casi vi era una significativa discrepanza tra i risultati teorici e quelli sperimentali proposero tra i primi delle formulazioni empiriche per il calcolo dei coefficienti di efflusso e successivamente si concentrarono sugli effetti legati agli errori di forma.
L’utilizzo di coefficienti di efflusso appropriati è un aspetto di fondamentale importanza all’interno di un modello numerico di un cuscinetto ad aria in quanto consente di tenere conto del tipo di moto del fluido attraverso i fori (turbolento o laminare) e di effetti legati alla geometria del foro di alimentazione al fine di ottenere delle portate numeriche molto più vicine a quelle misurate durante le caratterizzazioni sperimentali.
Una formulazione empirica che tiene conto in modo piuttosto rigoroso di tutti questi fenomeni è stata proposta in [3].
In maniera ugualmente importante è utile valutare le performance di un cuscinetto sulla base di stime statistiche che possano tenere conto dei possibili errori geometrici sia della parte statorica che mobile costituenti il cuscinetto.
Infatti, anche in presenza di lavorazioni effettuate secondo elevati standard di precisione è necessario tenere conto che i valori di tolleranza risultano sempre essere comparabili con le dimensioni dei meati che di solito si utilizzano nelle convenzionali applicazioni di pattini o cuscinetti a gas.
Nonostante il vantaggio di avere un effetto che tende a ridurre l’influenza di imperfezioni superficiali delle superfici separate dal fluido (in gergo tecnico chiamato “averaging effect”) molti studi scientifici hanno rilevato l’importanza di studiare la correlazione tra le tolleranze macro e micro-geometriche relative alla geometria dei supporti e le prestazioni del sistema supportato.
Ad esempio, H. Yabe [4, 5] ha trovato una stretta correlazione tra il runout di un rotore e gli errori di circolarità sulla sua superficie e quella del cuscinetto radiale che lo supporta [4].
Altri studi simili sono anche stati effettuati considerando il caso di guide lineari supportate da pattini pneumostatici [5].
Nell’ultimo decennio, lo sviluppo di software di simulazione capaci di accoppiare simultaneamente più equazioni fisiche di diversa natura ha consentito di effettuare ulteriori passi in avanti per quanto concerne la modellazione numerica finalizzata alla progettazione di sistemi di qualsiasi natura.
Questa possibilità ha permesso di integrare i classici modelli di cuscinetti a gas basati sulla sola equazione di Reynolds con le equazioni proprie della meccanica strutturale e della termodinamica consentendo quindi di raggiungere un ancor più elevato grado di affidabilità.
Questo articolo descrive uno studio numerico-sperimentale effettuato all’interno del laboratorio di Supporti a gas del Politecnico di Torino al fine di valutare l’influenza di alcuni effetti come la planarità, l’inclinazione e le deformazioni della superficie di un pattino pneumostatico durante le sue condizioni di lavoro.
Banco prova e test sperimentali
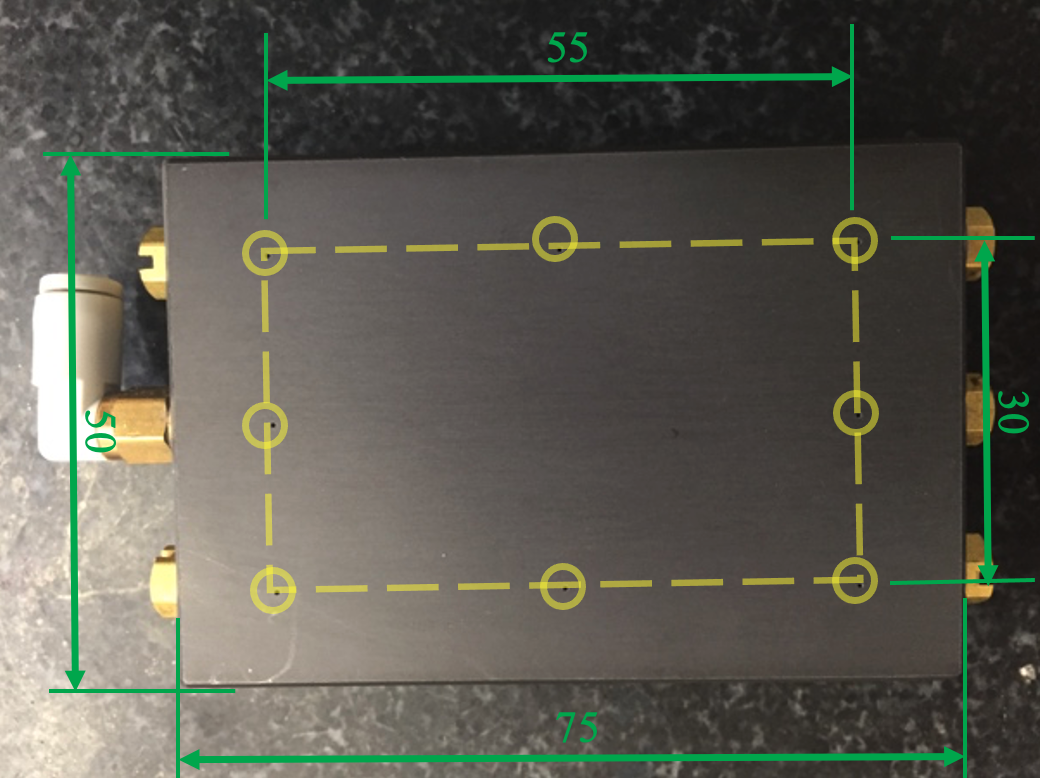
La figura 1 mostra una fotografia del pattino pneumostatico oggetto della sperimentazione. Il cuscinetto presenta una superficie attiva a base rettangolare di 75×50 mm2 con otto fori di alimentazione di diametro pari a 0,2 mm distribuiti lungo il perimetro di un rettangolo con dimensioni di 55×30 mm2.
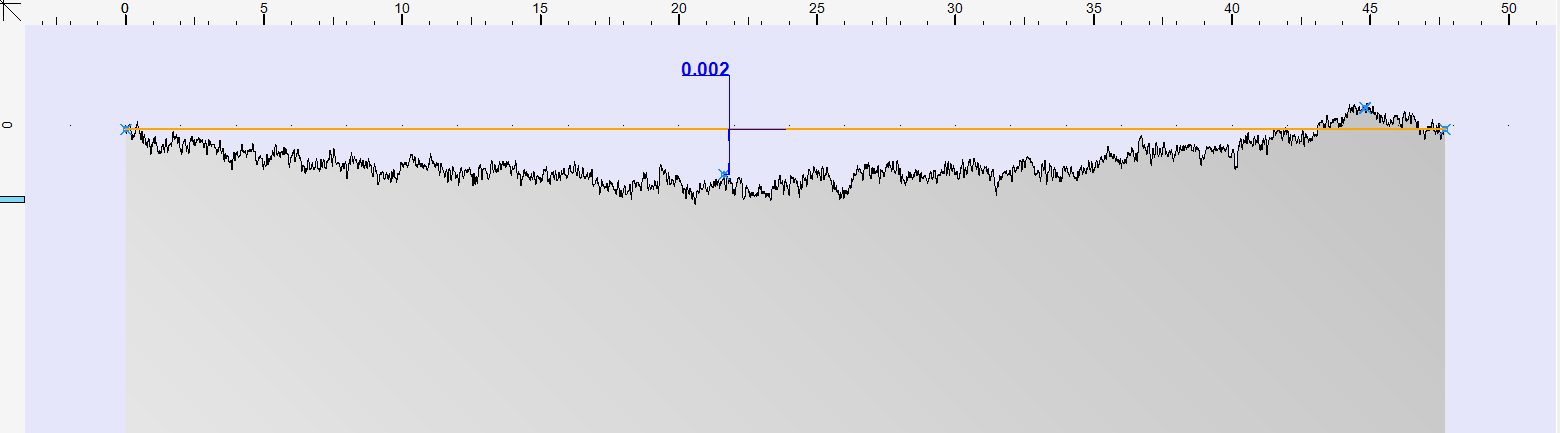
Al fine di valutare la corretta forma del meato sono state effettuate diverse misure del profilo della superficie attiva del cuscinetto. Una di queste è riportata in figura 1b, da cui è possibile notare l’evidente concavità della superficie del cuscinetto.
Le prestazioni statiche di tale pattino sono state testate su un apposito banco prova la cui fotografia e il cui schema sono visibili rispettivamente nelle figure 2a e 2b.

Come si può vedere dallo schema funzionale (fig.2b), il banco presenta una struttura che si estende verticalmente dal basso verso l’alto e presenta un basamento di acciaio sul quale viene posizionato il pattino in prova.
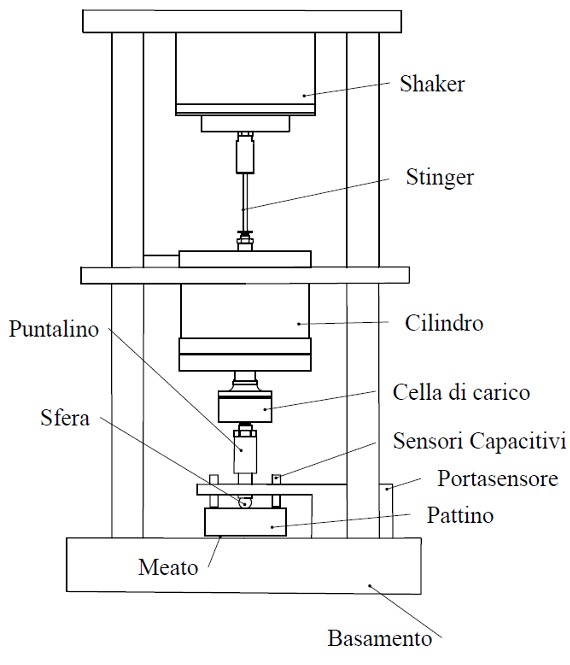
Fig. 2b – Schema del banco prova utilizzato durante la sperimentazione.
Questo viene caricato per mezzo di una “catena” di elementi collegati rigidamente in serie: un puntalino sferico, una cella di carico, un cilindro pneumatico, uno stinger e uno shaker.
I primi tre elementi permettono di trasmettere la forza statica generata dall’aria in pressione contenuta all’interno della camera del cilindro.
A questa forza statica, qualora fosse richiesto effettuare delle caratterizzazioni dinamiche, è possibile sovrapporre delle forzanti periodiche generate dallo shaker e trasmesse attraverso lo stinger il quale è rigidamente collegato allo stelo del cilindro.
Le caratteristiche di portanza (carico in funzione dell’altezza del meato), e consumo d’aria (portata in funzione dell’altezza di meato) sono ottenute variando gradualmente il carico applicato al pattino tramite il cilindro pneumatico e misurando contemporaneamente i corrispondenti valori di forza, portata e altezza di meato rispettivamente per mezzo della cella di carico, di un flussimetro e i quattro sensori capacitivi (fig. 2b).
È utile sottolineare che i valori di meato sono stati ottenuti in maniera indiretta come differenza dei valori misurati dai sensori capacitivi in presenza e in assenza di aria di alimentazione.
Il modello numerico
Il modello numerico del pattino descritto precedentemente è stato implementato mediante l’uso del software di simulazione multifisica COMSOL.
La parte di modello relativa al fluido è stata sviluppata in due parti.
La prima riguarda la modellazione del flusso d’aria che attraversa i fori di alimentazione del cuscinetto per poi arrivare all’interno del meato.
Secondo un classico approccio si è utilizzata la classica formula di un’espansione isoentropica (formula della portata attraversata da un ugello ideale) corretta mediante un’opportuna e ben nota formulazione del coefficiente di efflusso cd
dove, ds, ps e Ts rappresentano rispettivamente il diametro dei fori di alimentazione, la pressione e la temperatura del fluido a monte di essi.
R e µ sono il rapporto dei calori specifici e la viscosità dinamica dell’aria, p¯ = pc /ps è il rapporto tra le pressioni a valle e a monte dei fori di alimentazione cd ed è il coefficiente di efflusso che è stato espresso sia in funzione del numero di Reynolds Re che dell’altezza di meato h.
Queste equazioni sono state replicate per ogni singolo foro al fine di poter calcolare la portata in ingresso al meato Gin = 8∙Gforo in funzione delle variabili incognite pc (una per ogni foro).
La seconda parte del modello è quella che serve a calcolare le pressioni all’interno del meato: l’equazione di Reynolds isoterma.
La medesima equazione in COMSOL viene equivalentemente espressa come:
Dove p, vave e h sono rispettivamente i valori locali della pressione, velocità media lungo e altezza di meato in corrispondenza di ogni singolo nodo della griglia di calcolo.
Le componenti scalari della velocità media, che corrispondono alle portate volumiche per unità di profondità (qx, qy), possono essere calcolate a partire dal profilo di velocità come:
L’ultima equazione necessaria al fine di legare la prima e la seconda parte del modello è l’equazione di conservazione della massa applicata al meato:
dove Gout è la portata uscente dal meato in corrispondenza dei bordi del pattino.
Le equazioni descritte, insieme alle condizioni al contorno (pressione ambiente in corrispondenza del bordo del pattino) rappresentano un problema ai valori iniziali che risolto insieme alle equazioni della meccanica dei solidi permette di considerare l’interazione fluido-struttura e quindi la variazione della geometria del meato a seguito della deformazione.
Risultati
Il modello multifisico precedentemente descritto è stato utilizzato per quantificare l’accuratezza dei risultati numerici in correlazione con la presenza di possibili fattori macro-geometri come la planarità delle superfici, una loro possibile inclinazione (tilting) e la presenza di deformazioni dovute ai carichi applicati.
Queste valutazioni sono state effettuate ad un valore di pressione di alimentazione pari a 0,5 MPa relativi, essendo un valore di uso comune in molte applicazioni.
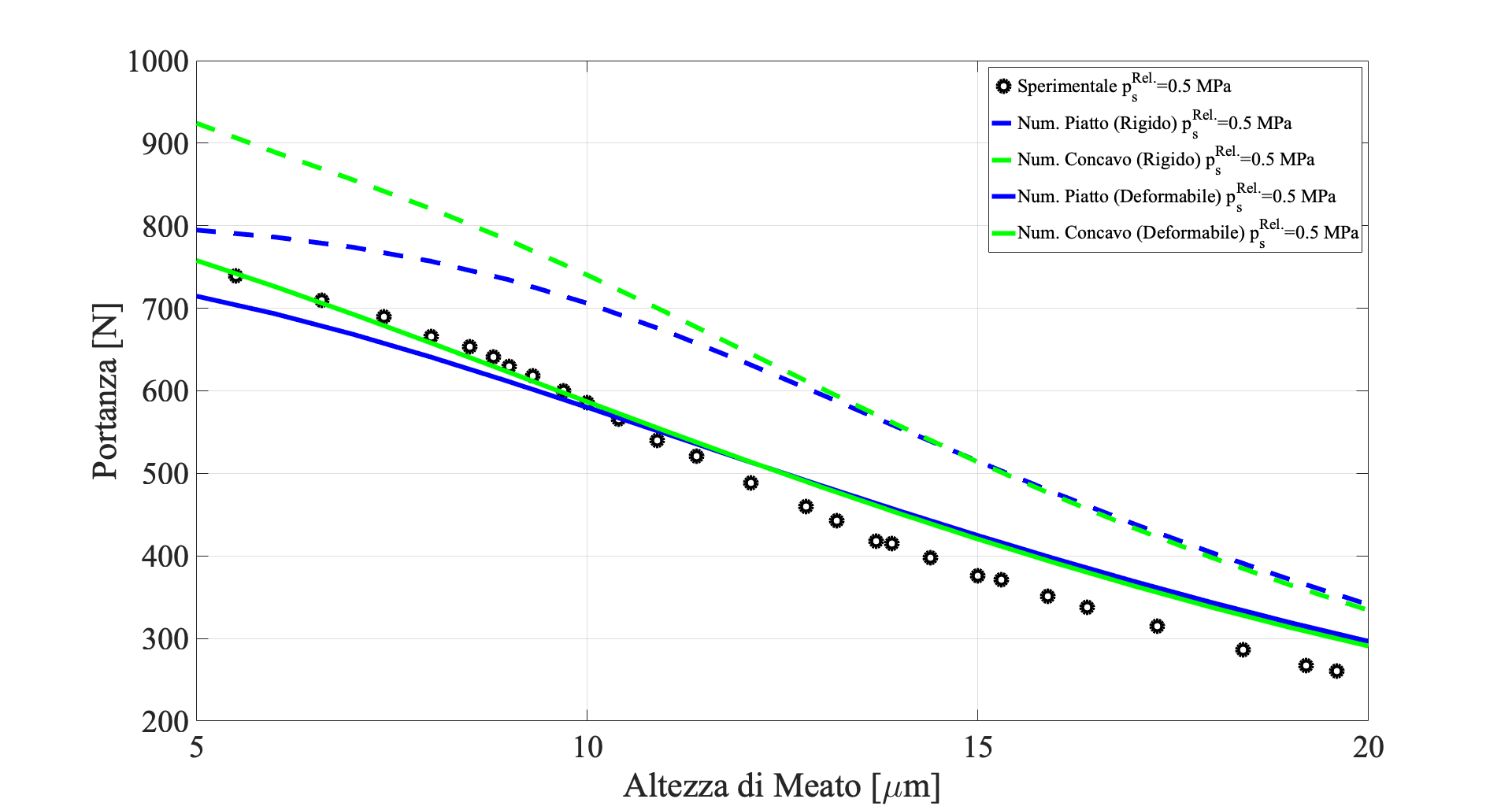
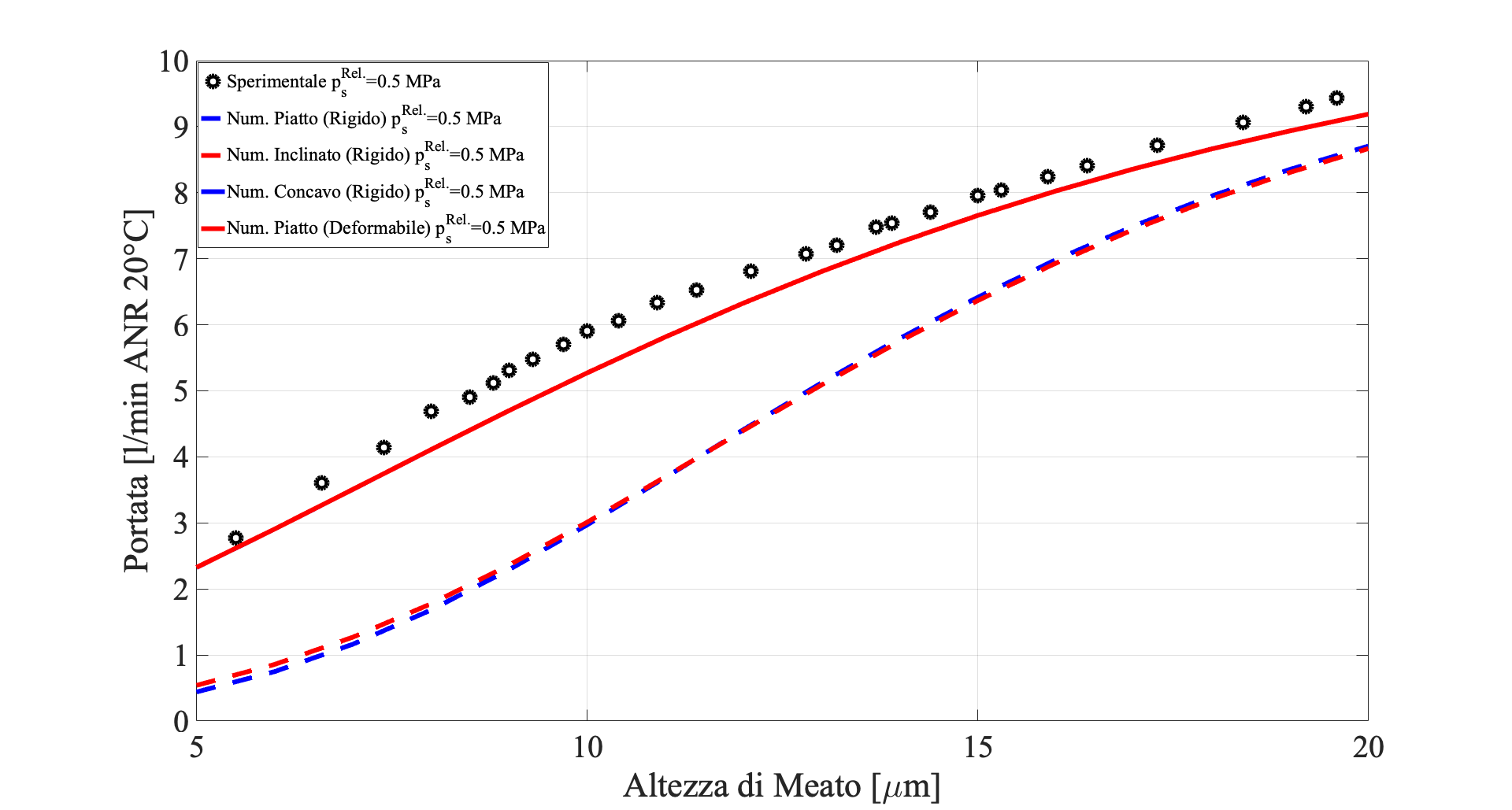
Le figure 5 e 6 comparano i risultati sperimentali con quelli di quattro modelli numerici differenti:
- pattino rigido con meato piatto
- pattino rigido inclinato
- pattino deformabile con meato piatto
- pattino deformabile inclinato.
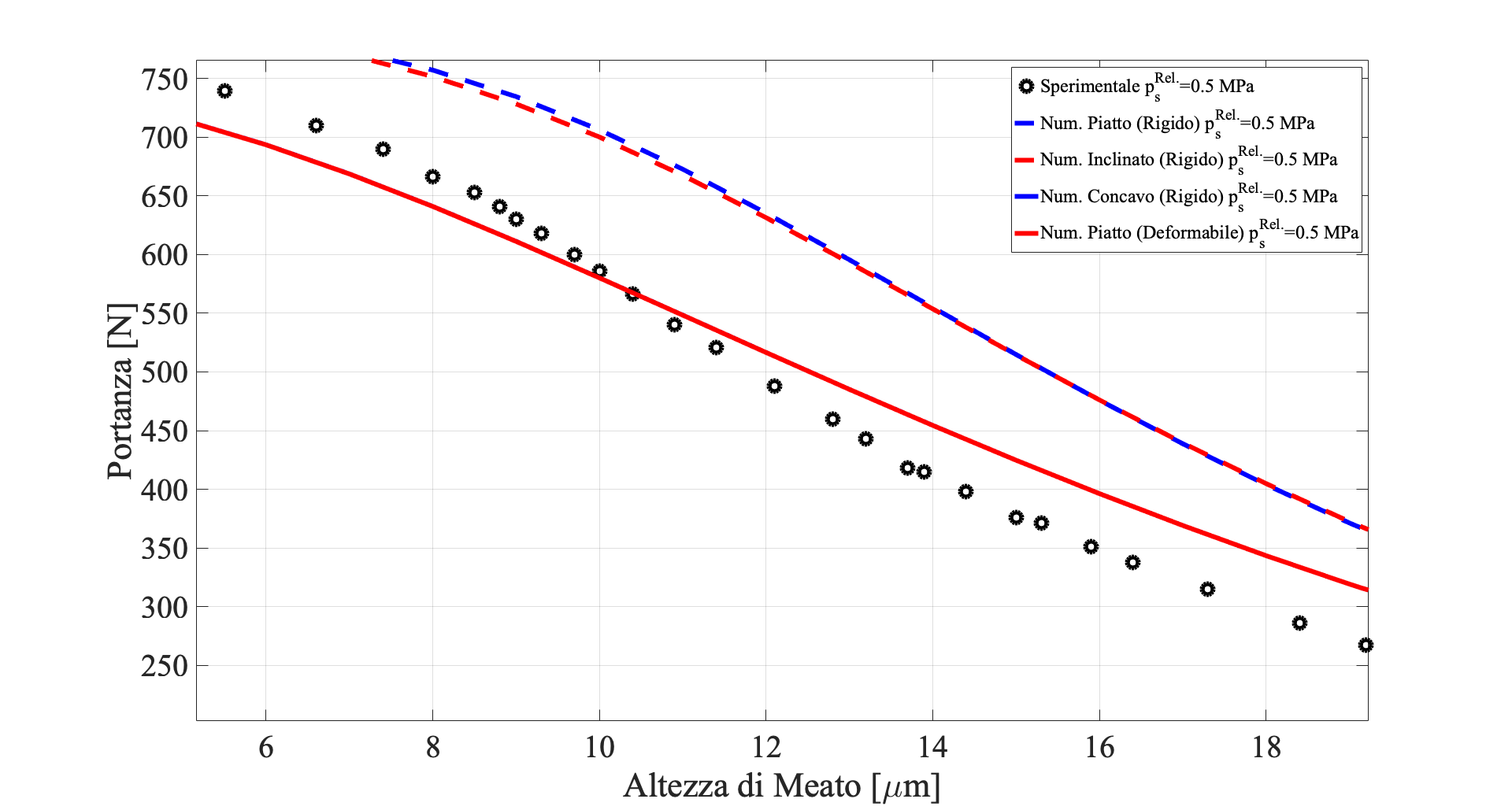
Confrontando le capacità di carico e i consumi d’ aria, appare evidente una significativa discrepanza tra i valori numerici e quelli sperimentali.
Questa si può facilmente spiegare avendo misurato a priori il profilo del cuscinetto, il quale presentava una certa concavità e sapendo inoltre che l’effetto delle deformazioni dovute al carico applicato non risultano essere affatto trascurabili rispetto ai valori di meato.
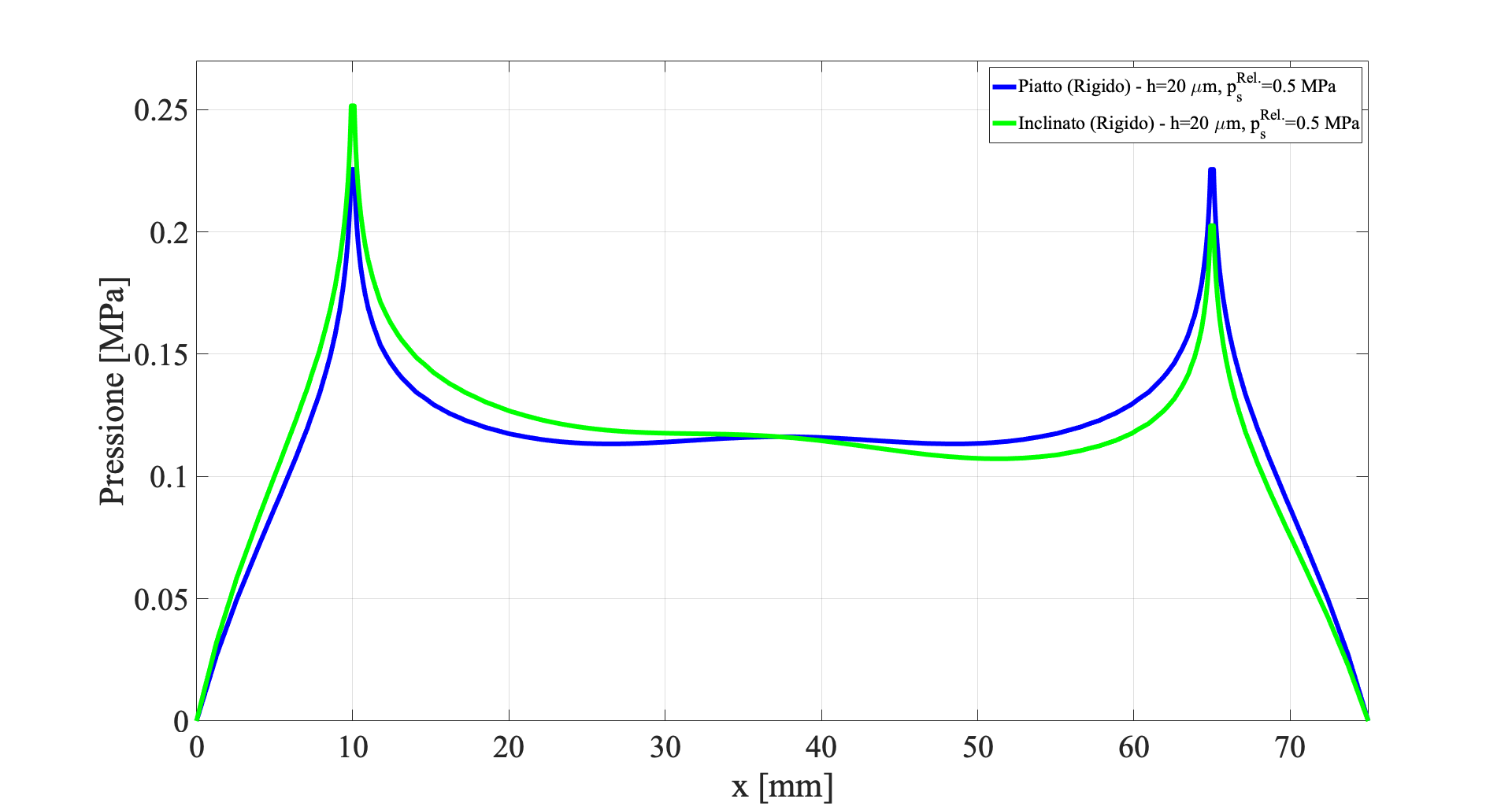
Considerando il pattino rigido, il confronto dei risultati numerici nel caso di meato piatto e inclinato evidenzia come un’inclinazione statica non porti a nessun significativo cambiamento delle caratteristiche globali del cuscinetto.
Questo aspetto si può facilmente spiegare analizzando la distribuzione di pressione (fig. 7) che in presenza di un’inclinazione della superficie del pattino diventa asimmetrica ma, una volta integrata, fornisce gli stessi valori di portanza e consumo d’aria del caso di superficie piana.
È poi importante notare che, nei casi in cui è stata considerata l’interazione fluido struttura (caso di pattino deformabile), i risultati numerici tendono ad avvicinarsi notevolmente a quelli sperimentali.
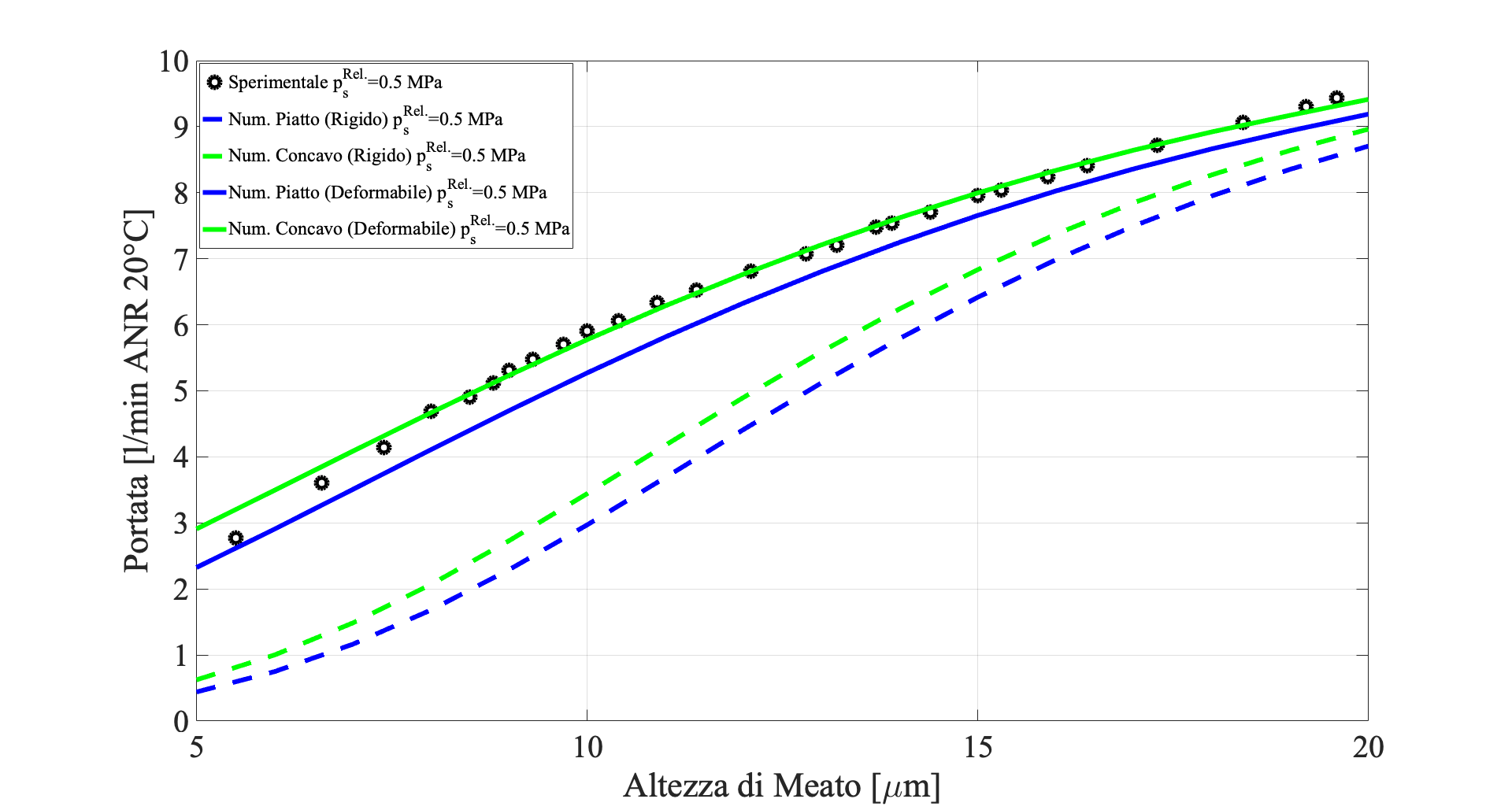
Infine, come si evince dai confronti mostrati nelle figure 9 e 10, i migliori match tra le curve numeriche e quelle sperimentali si ottengono quando, oltre che a considerare l’interazione fluido struttura, si vada a modellare un profilo di meato quanto più simile a quello reale.
In questo caso, il profilo è stato modellato come piatto nelle regioni in prossimità dei bordi e concavo in quella centrale, dato che, come detto precedentemente, il pattino presentava una marcata concavità con dei valori massimi di circa 2 micrometri (fig. 1b).
In conclusione
In questo articolo è stata esposta una breve panoramica sull’influenza dei difetti di produzione e montaggio di cuscinetti a gas in correlazione alle loro prestazioni. Tramite l’utilizzo di un software di simulazione multifisica è stato possibile verificare e quantificare l’effetto di fattori che molto spesso vengono trattati come secondari: errori di montaggio, caratteristiche delle superfici e l’interazione fluido struttura, con pattino deformabile. Il confronto dei risultati numerici e sperimentali ha dimostrato che soprattutto l’interazione fluido-struttura non possa essere trascurata qualora si voglia garantire un sufficiente standard di accuratezza in relazione al livello tecnologico raggiunto nelle odierne applicazioni in cui vengano utilizzati cuscinetti a gas.
Bibliografia
[1] Pink, E. G. “Investigations into design methods for externally pressurized gas journal bearings.” Tribology 7.6 (1974): 265-269. [2] Pink, E. G., and K. J. Stout. “Orifice restrictor losses in journal bearings.” Proceedings of the Institution of Mechanical Engineers 193.1 (1979): 47-52. [3] Belforte, G., Raparelli, T., Viktorov, V., & Trivella, A. (2007). Discharge coefficients of orifice-type restrictor for aerostatic bearings. Tribology International, 40(3), 512-521. [4] Yabe, Hiroshi. “A study on run-out characteristics of externally pressurized gas journal bearing: Rotor run-out characteristics.” JSME international journal. Ser. C, Dynamics, control, robotics, design and manufacturing 37.2 (1994): 355-361. [5] Yabe, Hiroshi, and Yasuyuki Ikuno. “A study on sliding accuracy characteristics of an externally pressurized gas-lubricated guide way: fundamental sliding accuracy characteristics.” JSME international journal. Ser. C, Dynamics, control, robotics, design and manufacturing 39.2 (1996): 371-377.






