In questo articolo si esporranno i calcoli più comuni che servono per definire alcuni elementi del profilo del dente del creatore
I più comuni calcolo necessari per definire alcuni elementi del profilo del dente del creatore sono:
calcolo del profilo normale; calcolo dell’angolo di pressione minorato nei creatori; calcolo del profilo di semitopping; calcolo di verifica per l’utilizzo del semitopping.
Calcolo del profilo dei denti del creatore: profilo normale
Chiamiamo profilo normale quel profilo che non ha modifiche particolari, quali protuberanza o semitopping o altre correzioni di forma.
Consideriamo inoltre che la cremagliera di riferimento abbia la linea primitiva tangente al diametro primitivo teorico dell’ingranaggio e che quindi l’angolo di pressione sia quello nominale dell’ingranaggio.
È necessario precisare questo perché poco più avanti si parlerà dei cosiddetti creatori ad angolo di pressione minorato, che, pur avendo i fianchi dei denti con un’inclinazione diversa da quella nominale dell’ingranaggio, eseguono egualmente il profilo voluto.
Supponiamo di dover dentare un certo ingranaggio avente:
modulo m
angolo di pressione α0
spessore circolare S0
dedendum hf
addendum h0
diametro primitivo d0
Il creatore dovrà avere l’addendum: hkw = hf

Dovrà avere lo spessore del dente sulla linea primitiva Sw uguale allo spessore circolare del vano del dente, che è a sua volta uguale al passo meno lo spessore circolare del dente.

L’inclinazione del fianco del dente del creatore sarà uguale all’angolo di pressione α0.
Se l’ingranaggio non è semitopping o topping, l’altezza totale Hw dovrà essere maggiore dell’altezza totale del dente dell’ingranaggio.
Hw > hk + hf (2)
Il profilo del dente del creatore dipende anche dalla spoglia frontale, che qualcuno chiama angolo di taglio.
Si tratta dell’angolo che il piano di affilatura fa con il piano che contiene l’asse del creatore (nel caso di solchi di affilatura paralleli all’asse).
Questo angolo, nella stragrande maggioranza dei casi, è di zero gradi. Cioè il piano di affilatura passa sull’asse del creatore.
Il motivo fondamentale di questa scelta è che solo in questo modo il profilo del creatore resta costante nelle successive affilature.
Un altro motivo importante è che per poter affilare i creatori che hanno un angolo di spoglia anteriore diverso da zero, bisogna portare la mola dell’affilatrice fuori asse di una quantità non sempre uguale, ma che è legata a diametro effettivo del creatore dalla semplice relazione:
tgγ = a/(D/2) = 2a/D (3)
Nel caso γ di positivo la mola sarà spostata sottocentro, nel caso di γ negativo la mola lavorerà sopracentro (figura 2).

Il valore di a deve essere quindi calcolato di volta in volta in funzione del diametro effettivo del creatore.
L’angolo di spoglia positivo si adotta quando si devono tagliare materiali particolarmente teneri, come per esempio alluminio, o acciai molto malleabili, avendo a disposizione solo dentatrici che non possono lavorare ad alta velocità di taglio.
Con un angolo di spoglia γ positivo si riduce lo sforzo del tagliente e si migliora la sua azione di taglio, ma contemporaneamente si indebolisce il tagliente in quanto la forza di taglio, che è sempre ortogonale alla superficie della faccia di taglio, ha una direzione sfavorevole, cioè tende a scheggiare il tagliente stesso.
Il fatto che la forza di taglio si riduce ha anche come diretta conseguenza una più lenta formazione del cratere d’usura sul petto del dente, ma sfortunatamente, esso è più vicino allo spigolo tagliente, aumentando quindi la possibilità di scheggiature precoci.
Considerazioni opposte si possono fare riguardo l’angolo γ negativo. In questo caso il tagliente si irrobustisce, il cratere si forma più velocemente ma in una posizione arretrata e gli spigoli taglienti sono in un certo senso protetti.
La spoglia fortemente negativa si applica generalmente sui creatori in metallo duro (carbide) del tipo skiving, che eseguono operazioni di finitura su ingranaggi già temprati.
Il creatore costruito con un angolo γ diverso da zero, deve essere progettato e costruito con un angolo di pressione che non è uguale all’angolo di pressione normale dell’ingranaggio.
La relazione che si deve applicare per calcolare l’angolo di pressione del creatore è la seguente:

Dove:
αon1= angolo di pressione costruttivo del creatore
αon= angolo di pressione normale dell’ingranaggio
γ = angolo di spoglia frontale
x = angolo di spoglia sul fianco
Nella costruzione di un creatore nuovo va considerato il segno più nel caso di angolo di spoglia positivo ed il segno meno nel caso di angolo di spoglia negativo.

Il problema dell’interferenza
Tra due ruote dentate che si accoppiano può generarsi un’interferenza, cioè lo spigolo di testa di una ruota può interferire con la base del dente dell’accoppiante rendendo precaria o impossibile la rotazione.
A questo fenomeno non fugge nemmeno lo speciale accoppiamento tra un ingranaggio ed una cremagliera che, bisogna ricordarlo, è un ingranaggio con un numero di denti infinito.
Se consideriamo ora che i denti del creatore costituiscono una cremagliera, può accadere che in determinate circostanze si generi il fenomeno dell’interferenza che all’atto pratico produce un sottointaglio alla base del dente (figura 4).
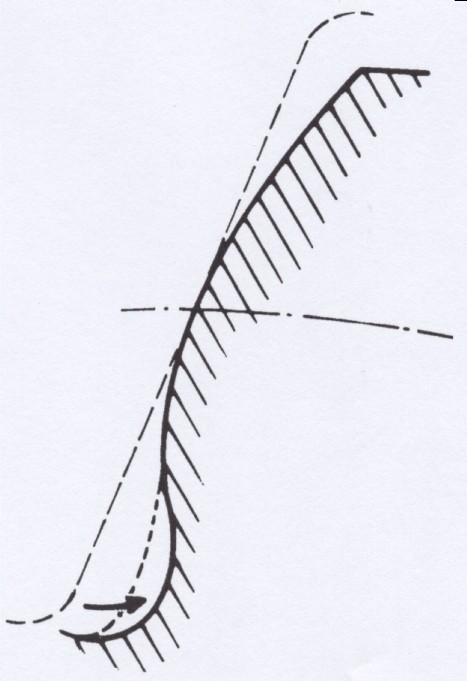
Questo fatto fino ad un certo punto può essere considerato positivo dal punto di vista della geometria del dente, in quanto il sottointaglio fa le funzioni dello scarico che normalmente è generato dalla protuberanza per facilitare le operazioni di finitura dei denti. Se però il sottointaglio è troppo grande, riduce il profilo attivo del dente al punto da ridurre considerevolmente la linea di ingranamento tra ingranaggio e controruota.
Oggi, vengono progettate delle scatole cambio più piccole rispetto il passato anche per trasmettere potenze relativamente grandi; in questi casi vengono richieste lunghe linee di ingranamento con la massima lunghezza del profilo attivo.
L’inizio del profilo attivo (TIF) è su un diametro molto prossimo al diametro di fondo dente e quindi non sono ammessi sottointagli generati dall’interferenza.
Un altro grave problema è costituito dal fatto che nella zona di interferenza si ha un’asportazione maggiorata di materiale da parte di ogni dente, con un aumento dello spessore del truciolo e, quindi, della sollecitazione di ogni singolo dente del creatore.
Il fenomeno dell’interferenza tra due ingranaggi dipende dall’angolo di pressione, dal rapporto di trasmissione e dall’addendum previsto sugli ingranaggi.
Se consideriamo un dimensionamento normale, con l’addendum dell’ingranaggio uguale al modulo, cioè:
h0 = k ・m
con k=1 e nel caso dei creatori, dove Z1 è infinito, cioè dove si ha:
Z2/Z1 = 0
si può usare il diagramma della figura 5 per trovare il numero minimo di denti per cui si genera una certa interferenza che può permettere l’uso del creatore senza protuberanza.

Creatori con angolo di pressione minorato
È necessario fare prima di tutto una premessa.Il modulo e l’angolo di pressione, specie sui creatori, sono dei valori convenzionali che possono essere cambiati entro ampi limiti senza modificare sostanzialmente i risultati sul pezzo prodotto.
Il fatto è che normalmente si sceglie come cerchio di rotolamento il diametro primitivo dell’ingranaggio. Si fa coincidere quindi il diametro primitivo di funzionamento con il diametro primitivo nominale dell’ingranaggio, ma questa è una scelta non obbligatoria; in teoria si può scegliere come diametro primitivo di funzionamento, cioè come cerchio su cui rotolare, un qualsiasi diametro dell’ingranaggio.
Sarà sufficiente considerare i valori che derivano da questa scelta e cioè il nuovo valore di passo e quindi di modulo, il nuovo valore dell’angolo di pressione ed il nuovo valore dell’elica.

La figura 6 mostra, accanto all’ingranaggio standard, lo stesso ingranaggio in cui si considera prima un diametro primitivo più piccolo e poi un diametro primitivo più grande.
Facciamo l’esempio di un ingranaggio a denti diritti con i seguenti dati nominali:
m = 2 mm; Z = 30; αon= 20°.
Il diametro primitivo sarà:

In corrispondenza a questo diametro si avrà l’angolo di pressione di 20°.
Il diametro di base di questo ingranaggio sarà:
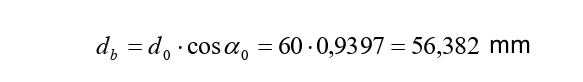
Supponiamo ora di considerare due casi, scegliendo come diametro primitivo dell’ingranaggio prima 59 e poi 61 mm.
Nella tabella 1 sono calcolati gli elementi fondamentali relativi a queste scelte, ma l’ingranaggio è sempre lo stesso: potremmo considerare anche i nuovi valori come quelli nominali!
| Valori nominali | Prima opzione | Seconda opzione | |
| m = p/ π (mm) | 2 | 1,9667 | 2,0333 |
| z | 30 | 30 | 30 |
| αo | 20° | 17°,1376 | 22°,4370 |
| do (mm) | 60 | 59 | 61 |
| db = do ・cos αo | 56,382 | 56,382 | 56,382 |
| cos αo = db / do | 0,9397 | 0,9556 | 0,9243 |
| P = π・do/Z | 6,2832 | 6,1785 | 6,3879 |
Precisato questo, e considerando che il fenomeno dell’interferenza di cui si è detto al punto precedente, è tanto maggiore quanto maggiore è l’addendum del creatore, cioè tanto maggiore è la distanza della testa del dente dal cerchio di rotolamento, ne deriva che per ridurre l’interferenza è sufficiente ridurre il valore dell’addendum del creatore.
In sostanza si tratta di rotolare su un cerchio più vicino al diametro interno dell’ingranaggio.
Se nell’esempio precedente ci fosse interferenza tra creatore e pezzo, questa sarebbe inferiore se si scegliesse l’opzione 1, mentre aumenterebbe se si scegliesse l’opzione 2.
Il creatore in questo caso dovrebbe avere l’angolo di pressione di 17°,1376 , cioè minore di quello nominale dell’ingranaggio.
Ecco quindi la ragione per cui si parla di creatori ad angolo di pressione minorato.
Il vantaggio maggiore che si ottiene usando questo tipo di creatore, oltre che a ridurre l’entità del sottointaglio e quindi di aumentare la lunghezza del profilo attivo, è quella di una minore sollecitazione sulla testa del dente con un aumento del rendimento del creatore stesso.
Un altro vantaggio è quello di ridurre il valore del raggio di raccordo a fondo dente, facilitando la progettazione e l’impiego dei coltelli rasatori.
Si può anche accennare al fatto che un creatore con un più basso angolo di pressione ha una minor tendenza a trasmettere gli errori di costruzione e di montaggio sul profilo del dente eseguito.
Si può anche fare la correzione opposta, perché in certi ingranaggi, il diametro primitivo è troppo vicino al diametro interno dell’ingranaggio o perfino inferiore. In questi casi si preferisce progettare il creatore con un angolo di pressione maggiorato alzando quindi il valore del cerchio di rotolamento.
Calcolo del profilo semitopping
Finora si sono usate formule matematiche che contenevano solo funzioni trigonometriche, ma ora, per il calcolo del profilo semitopping è necessario introdurre una nuova funzione, molto usata nel campo degli ingranaggi: cioè la funzione invα. Per far questo riportiamo anche la definizione di evolvente di cerchio, che, come tutti i tecnici sanno, è la forma che hanno i denti degli ingranaggi cilindrici usati normalmente nelle trasmissioni. L’evolvente di cerchio è il luogo dei punti descritto dall’estremità di una semiretta che rotola senza strisciare sopra un cerchio di raggio Rb detto cerchio di base (figura 7).

Tutti i denti degli ingranaggi cilindrici hanno il profilo che è una porzione di evolvente di cerchio. Questa curva ha alcune interessanti proprietà:
– il segmento PQ ha la stessa lunghezza dell’arco di cerchio O1Q;
– tutte le rette del tipo PQ, che collegano un generico punto P dell’evolvente al cerchio, sono tangenti al cerchio stesso;
– le stesse rette sono sempre ortogonali all’evolvente.
Inoltre, sempre con riferimento alla figura 7, si possono scrivere le seguenti relazioni.

Questa è la funzione involuta dell’angolo α.
α è detto l’angolo di pressione dell’evolvente nel punto P, cioè riferito al raggio R. Si ha ancora l’importante relazione:
Rb = R cosα
Tutte le moderne calcolatrici danno il valore della funzione
invα = α – tgα
Gli ingranaggi hanno, quasi sempre, gli smussi sulla sommità dei denti che preservano gli spigoli da ammaccature e bavature che renderebbero l’ingranaggio rumoroso.
I creatori che eseguono gli smussi sulla sommità dei denti sono detti semitopping.
Lo smusso si ottiene sagomando opportunamente il fondo dei denti del creatore.
Le due quote che bisogna calcolare sono: l’inclinazione γps della parte del creatore che esegue lo smusso e la distanza K dell’inizio smusso dalla retta primitiva (figura 8).
In sostanza lo smusso sull’ingranaggio, avente una certa inclinazione γx e l’inizio sul raggio Rx, è una porzione di evolvente che ha un certo raggio di base Rbx.
È importante calcolare lo spessore circolare del dente sul raggio inizio smusso Rx, cioè l’arco tra i punti Q e Q1. Si calcola con la seguente espressione:

Il creatore ha sempre la stessa linea primitiva tangente al cerchio primitivo di raggio Rp .
La parte che esegue lo smusso è come se dovesse lavorare un ingranaggio con raggio primitivo uguale a Rp e che deve fare un angolo di pressione γx nel punto Q (sul raggio Rx). Si ha quindi:
Rbx = R・cos γx
Raggio base dell’evolvente di cui lo smusso è parte.
cos γpx = Rbx /Rp
in cui γpx è l’angolo di pressione sul diametro primitivo, cioè sul punto Px . Questa è perciò l’inclinazione del tratto di creatore che deve fare lo smusso.
Si può calcolare la distanza K:

L’ampiezza dello smusso sull’ingranaggio resta costante nelle successive affilature del creatore, perché, come si è detto, il creatore è sostanzialmente una fresa a profilo costante in virtù della particolare curva della spoglia del dente.
Tuttavia ci sono alcune considerazioni da fare riguardo le varie tolleranze che entrano in gioco e che rendono molto difficile una effettiva costanza dello smusso.
Il primo luogo c’è la tolleranza di costruzione del creatore stesso, sia per quanto riguarda lo spessore del dente, sia per quanto riguarda la quota d’inizio smusso K e sia per quanto riguarda l’angolo γpx.
Poi c’è la tolleranza sullo spessore cordale del dente dell’ingranaggio in fase di dentatura, che consente al creatore di avvicinarsi un po’ di più o un po’ di meno al pezzo. Infine c’è la tolleranza sul diametro esterno dell’ingranaggio.

È evidente che se il raggio di inizio smusso Rx resta costante, al variare del raggio esterno Re l’ampiezza dello smusso varia sensibilmente.
Qualche volta può portare all’annullamento, o quasi, dello spessore di testa, cioè dello spessore del dente sul diametro esterno. In questo caso i due smussi, destro e sinistro, si intersecano sul diametro esterno. Ciò non è mai tollerato.
In alcuni casi, specie se si tratta di ingranaggi con piccolo modulo (ad esempio: m=1 oppure m=1,25), si usa il cosiddetto creatore topping.
Si tratta di costruire il profilo del dente del creatore in modo che, oltre a fare gli smussi, lavori anche sul diametro esterno. In questo caso si ha la certezza che in testa al dente ci sarà sempre un tratto piano.
Calcolo di verifica per l’utilizzo del semitopping
I creatori semitopping sono previsti per ottenere uno smusso con una stabilita entità radiale e con una data inclinazione su ruote dentate aventi un numero di denti prefissato.
Un creatore di questo tipo, perciò, eseguirà uno smusso esattamente come previsto solo sull’ingranaggio per il quale è stato calcolato.
Se si vuole tagliare un altro ingranaggio, con uguali caratteristiche ma con un numero di denti diverso, varieranno il valore dello smusso e la sua inclinazione; entro certi limiti questa variazione può essere tollerata.
Il valore dello smusso aumenta se aumenta il numero di denti dell’ingranaggio da dentare rispetto a quello per cui il creatore è stato calcolato, e viceversa.
Stabiliti i limiti entro i quali l’entità dello smusso può essere tollerato, il procedimento di verifica che viene esposto permette di stabilire se il creatore eseguirà lo smusso entro questi limiti.
Noti i valori di K, αon, γpx., m del creatore e noto il numero di denti Z dell’ingranaggio sul quale si deve effettuare lo smusso, si ha:
Rp= m・Z/2 raggio primitivo della dentatura
Rb= Rp・cosαon raggio del cerchio base della dentatura
RbI= Rp・cosαγpx. raggio del cerchio base dello smusso
Si può allora calcolare:

Stabiliti i valori massimo e minimo del valore radiale dello smusso Cmax e Cmin si trovano i rispettivi diametri di inizio smusso.
Rx1= Re – Cmax ed Rx2 = Re – Cmin
E quindi si possono calcolare i valori degli angoli di pressione dello smusso e dell’evolvente in corrispondenza a questi diametri.
cosαγpx1 = Rb’/ Rx1 cosαx1 = Rb’/ Rx1
cosαγpx2 = Rb’/ Rx2 cosαx2 = Rb’/ Rx2
Infine si calcola il valore del parametro A’:
A1’ = invγpx1 – invαx1
A2’ = invγpx2 – invαx1
Si ha allora:
per Cmax deve essere A1’ >=A
per Cmin deve essere A2’ >=A
Se queste relazioni sono soddisfatte il creatore può essere utilizzato in quanto eseguirà lo smusso entro i limiti che sono stati fissati.






