Le fasi di realizzazione di una “buona” coppia di ruote dentate sono la progettazione, la produzione, il controllo e il collaudo. Questo flusso di lavoro è chiamato “closed loop”. Alcuni esempi di closed loop per ingranaggi conici, cilindrici e a vite senza fine
Le fasi di realizzazione di una “buona” coppia di ruote dentate sono la progettazione, la produzione, il controllo e il collaudo. Ognuna di queste fasi fase si ripercuote sulla successiva e l’ultima si ripercuote sulla prima e così via. Questo flusso di lavoro è valido in diverse applicazioni, dai riduttori a gioco ridotto alle trasmissioni automobilistiche e ai riduttori industriali o per il sollevamento off-shore. Questo flusso di lavoro è chiamato “closed loop”.
Nell’articolo ne verranno presentati alcuni esempi per ingranaggi conici, cilindrici e a vite senza fine:
– scambio di informazioni tra l’ufficio tecnico e il controllo qualità per confrontare la microgeometria progettata, stimata e realizzata e LTCA;
– generazione di diagrammi del profilo per i disegni che possono essere modificati dal progettista in caso di deroghe su requisiti non rispettati ma accettabili;
– stima del twist causata dal processo di fabbricazione.
Il concetto di Closed Loop
Closed-loop è una espressione molto usata negli ultimi anni, soprattutto in relazione al concetto di Industria 4.0 [1]. Tale espressione verrà usata in questo articolo in riferimento alla relazione fra specifica e verifica (figura 1) come definito dal GPS (Geometrical Product Specifications) nelle norme ISO [3], a partire dalla ISO 1 [2], la “madre” di tutte le norme.
Il processo di progettazione di un ingranaggio prevede varie fasi, come l’analisi delle richieste del mercato, il dimensionamento di massima con formule, la verifica numerica e l’ottimizzazione [4], ma deve terminare con la realizzazione di un disegno che fornisca indicazioni chiare e incontrovertibili a chi deve realizzare il pezzo. È quello che si definisce una specifica.
D’altro canto, anche la produzione dell’ingranaggio passa da più fasi (forgiatura, taglio, trattamenti termici, finitura), ma deve terminare con il controllo che quanto realizzato sia aderente a quanto richiesto. È quello che si definisce verifica.
Se la specifica si concretizza un disegno bidimensionale con quote, tabelle e simboli realizzato in 2D a CAD, la verifica confluisce in un report con grafici e tabelle prodotto da una macchina CMM (“tridimensionale”) o GMM (evolventimetro) o compilato da un operatore che ha preso delle misure con hard-gauging (calibro, micrometro, ingranometro).
Il closed loop richiedere che specifica e verifica siano entrambi completi e senza.
Ad esempio, non può essere definita come una vera e propria specifica il disegno di una ruota in cui vengono riportati solo numero di denti, modulo (senza specificare se normale o trasversale) ed elica, ma neppure può esserlo il disegno la cui tabella riporta valori di misura cordale e misura fra i rulli non coerenti fra loro.
Allo stesso modo la consegna di un lotto di ruote dentate senza report di controllo qualità non può essere considerato una verifica.
Di seguito, verranno presentati alcuni esempi di closed loop fra progettazione e produzione per ruote cilindriche, coniche e per viti senza fine.
Ingranaggi conici
Storicamente, il closed loop nell’ambito degli ingranaggi è nato per quelli conici. Il processo di taglio classico delle ruote coniche, face-milling o face-hobbing, prevede intrinsecamente una messa a punto del contatto tramite i parametri della macchina utensile che è esso stesso un closed loop. Le moderne tecniche di simulazione del contatto prima della verifica sul tester (figura 2) hanno velocizzato i tempi di produzione, ma il concetto è rimasto pressoché invariato come descritto da [5] e [6].
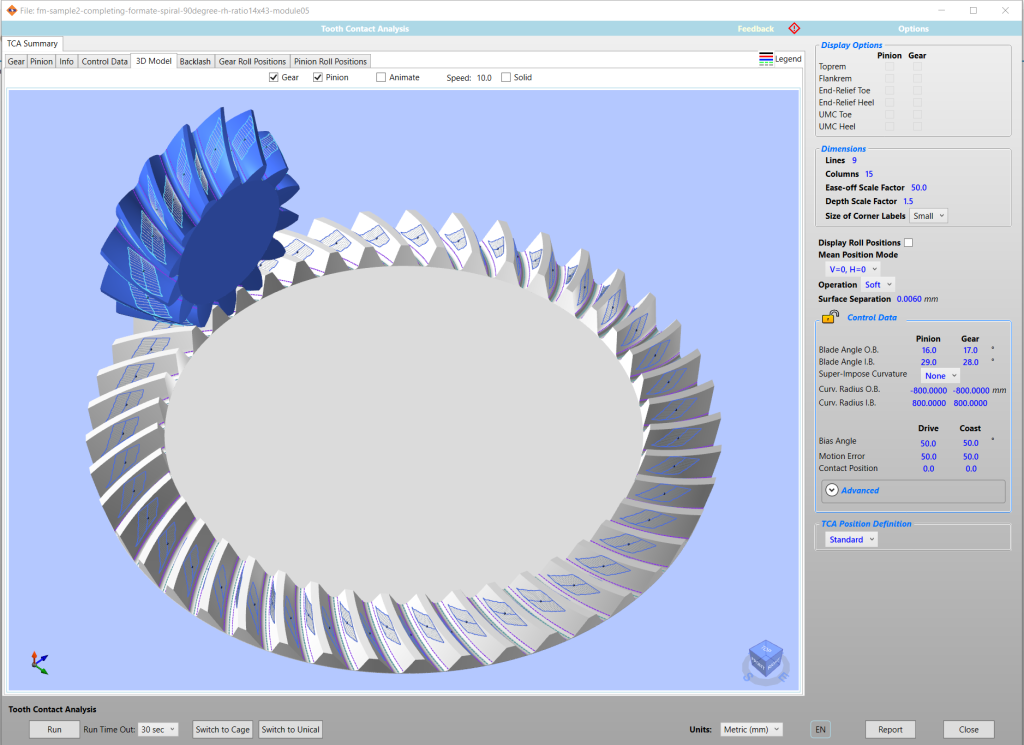
Non tutti i progettisti di coppie coniche dispongono però di questi software dedicati alle macchine utensili.
In questo caso seguono le orme di Socrate: sanno di non sapere. Possono limitarsi a definire, in prima battuta, solo modulo e numero di denti, oltre ai valori praticamente standard di angolo di pressione (che è spesso 20° o 22.5°), angolo di spirale (quasi sempre 35°) e larghezza di fascia (circa 1/3 della lunghezza della generatrice). È quasi imbarazzante pensare che lo spessore del dente e il raggio di fondo dente, così curati per le ruote cilindriche e così importanti per il calcolo della resistenza a flessione, vengano ignorati nella fase di progettazione delle ruote coniche.
Il più delle volte, il progettista di coppie coniche che non dispone del software dedicato alla macchina utensile “tenta di indovinare” quali saranno gli angoli di testa, e fondo, oltre allo spessore del dente, magari “sperando” in un raggio pieno per il fondo dente. Attualmente, la fonte bibliografica liberamente accessibile che arriva a definire più realisticamente la geometria finale di uno spiral face milling è [9]
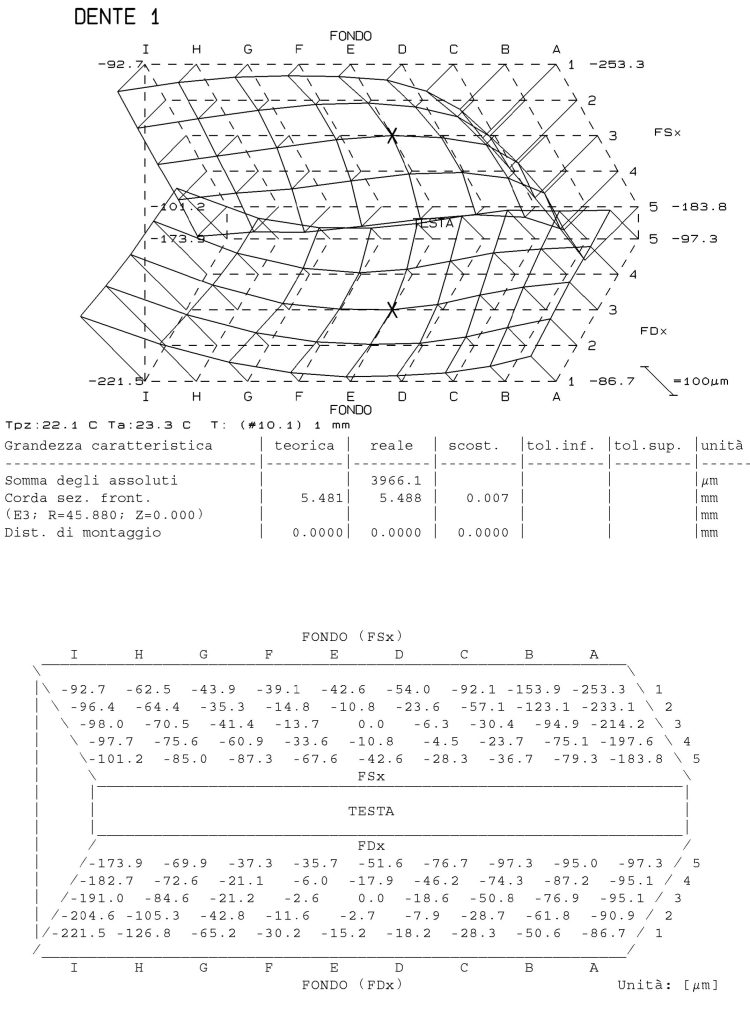
In certi casi il disegno viene realizzato in due tempi e tiene traccia dell’effetto del closed loop, come quello riportato in figura 3. Nella metà superiore c’è la geometria definita dal progettista, nella metà inferiore c’è la geometria effettiva, dedotta dal dimension sheet generato dall’officina.
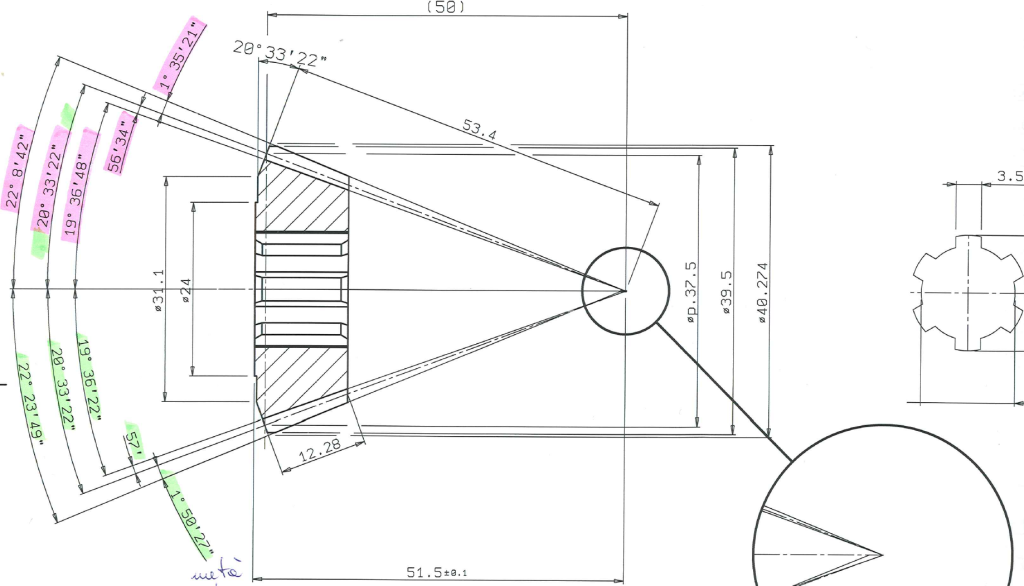
Questo primordiale closed loop per le coppie coniche, che si limita a intervenire sul processo di progettazione ancor prima di passare alla realizzazione dei componenti, cioè ad agire solo sulla definizione della specifica, si completa col passaggio della griglia di microgeometria rilevata dalla GMM al software di progettazione.
In altri casi, lo stesso disegno con i soli dati principali di dentatura viene consegnato a diversi fornitori. Molto probabilmente ciascuno di essi di solito taglierà la coppia conica con diversi parametri di taglio (tabella 1). Quella la stessa coppia conica sarà realizzata con geometrie diverse e avrà di conseguenza resistenze diverse. In casi come questo, l’ufficio tecnico non sarà in grado di generare un unico report di calcolo realistico e credibile della coppia conica per i clienti o per gli enti certificatori. In questo caso non si può parlare di closed loop.
| A | B | C | |
| Mean circular thickness pinion [mm] | 7.85 | 7.60 | 7.01 |
| Mean circular thickness gear [mm] | 3.10 | 3.40 | 3.98 |
| Whole depth | 8.09 | 8.40 | 8.09 |
| Edge radius used in strength – pinion [inch] | 0.015 | 0.020 | 0.040 |
| Edge radius used in strength – gear [inch] | 0.060 | 0.035 | 0.045 |
| Cutter radius [inch] | 3.000 | 3.750 | 3.000 |
| Geometry factor – Strength – J pinion | 0.2878 | 0.2831 | 0.2769 |
| Geometry factor – Strength – J gear | 0.2909 | 0.2861 | 0.3440 |
| Strength factor Q – pinion | 10.889 | 11.071 | 11.318 |
| Strength factor Q – gear | 2.74577 | 2.79255 | 2.32188 |
(13-51), modulo (4.126), larghezza di fascia (30 mm) e angolo di pressione (22.5°)
Ingranaggi cilindrici
Per gli ingranaggi cilindrici vengono ora riportati tre diversi casi applicativi.
Twist da fabbricazione
Il primo caso riguarda una trasmissione per automotive. È stato chiesto di verificare l’impronta di contatto sotto carico di una coppia di ingranaggi elicoidali.
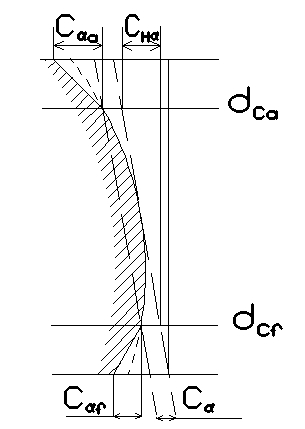
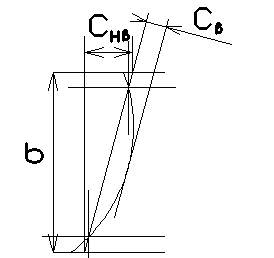
Dati il disegno delle due ruote e i cedimenti calcolati da un software multibody MBF, è stato chiesto di eseguire l’analisi di contatto sotto carico con diversi tipi di microgeometria:
- quella a disegno, che prevedeva sia bombatura di profilo che di elica (figura 4);
- quella stimata dal software di progettazione e analisi, che aggiunge un indesiderato ma inevitabile twist dovuto al processo di rettifica, se non compensato [10];
- quella stimata dal software della macchina di rettifica, applicando un metodo di parziale compensazione (figura 5);
- quella rilevata dalla GMM (figura 6).
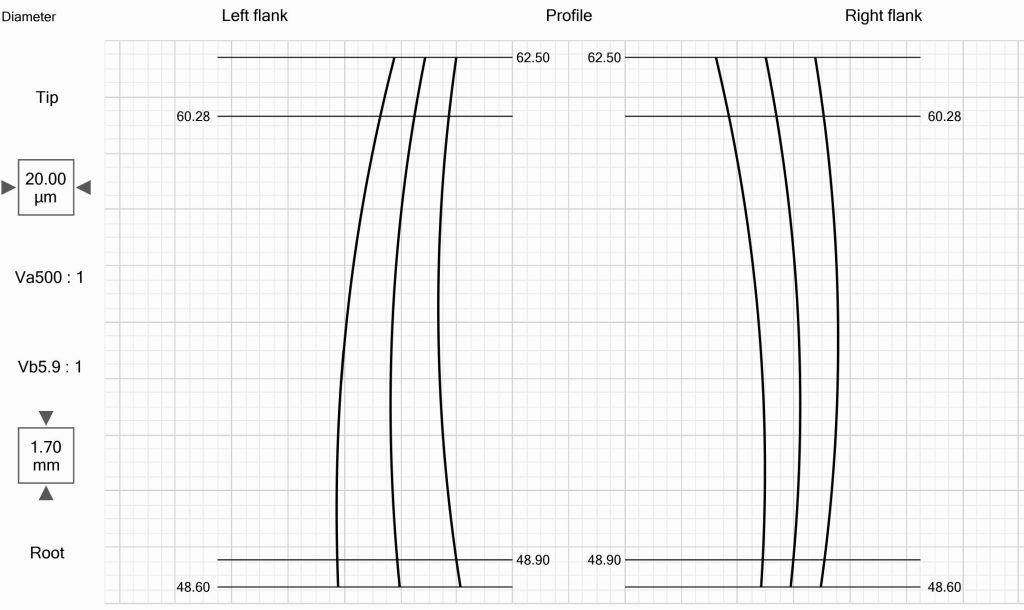
Le ultime due erano abbastanza simili per quanto riguarda il twist, ma la seconda aveva ovviamente un andamento più “sporco”. In entrambi i casi è stato possibile accedere alle griglie in un formato file importabile dal software di progettazione e analisi [11].
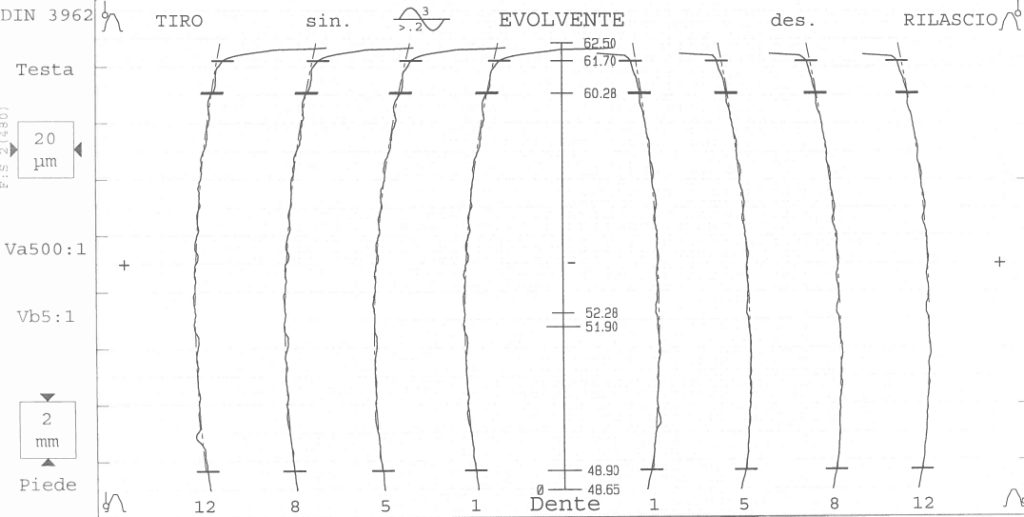
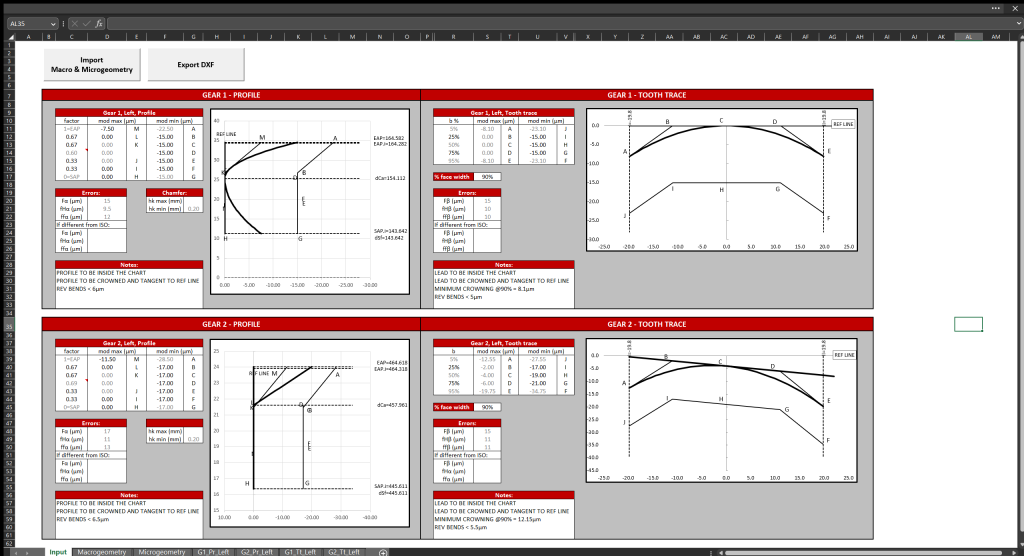
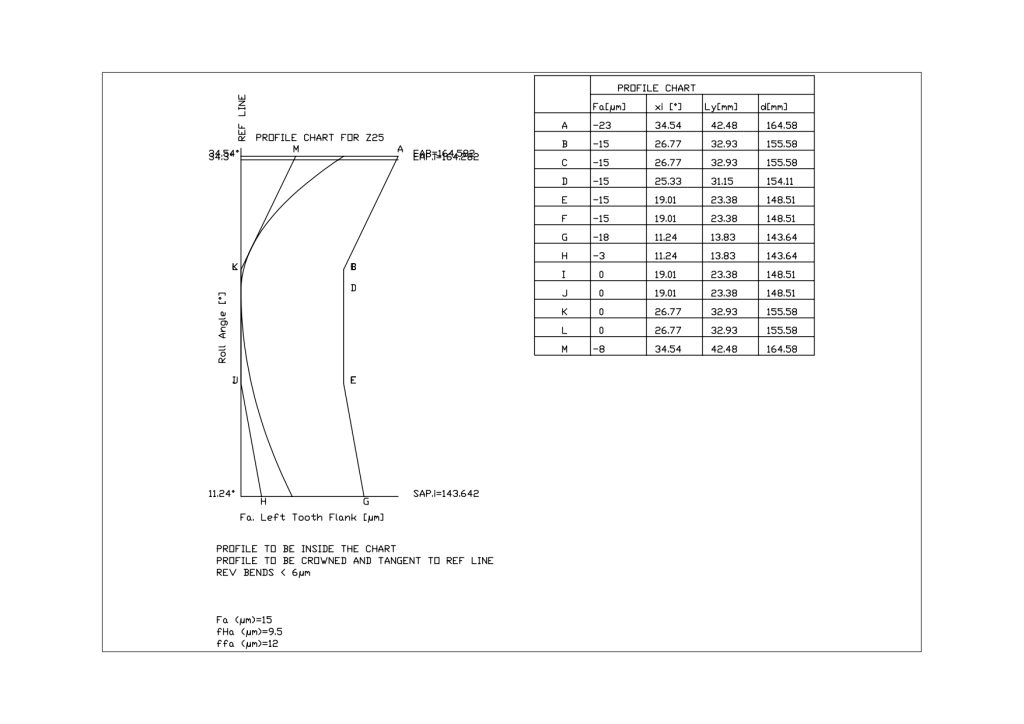
Grafico del profilo K
Il secondo esempio nasce dalla richiesta di avere uno strumento agile per disegnare e modificare il profilo K con libertà di rappresentazione della fascia di tolleranza.

L’esigenza del progettista era di poter verificare se scostamenti rilevati eccedenti la tolleranza richiesta fossero ancora accettabili. In tal caso l’ufficio tecnico procede con una deroga e quindi col il disegno della nuova area di tolleranza del profilo K. Ecco gli step di questo closed loop.
– Progettazione della coppia di ingranaggi cilindrici
– Realizzazione dei disegni costruttivi delle ruote, corredati dal profilo K con relativa area di tolleranza definita secondo le specifiche aziendali
– Realizzazione e misurazione del pezzo
– Nel caso di pezzo con misure eccedenti i limiti chiesti, LTCA con i nuovi estremi di tolleranza
– In caso di accettabilità dei risultati, definizione della deroga e aggiornamento della tavola con il nuovo profilo K.
Ondulazione (Waviness)
Il terzo case history riguarda la richiesta di limitare l’ondulazione del profilo, che alcune aziende stanno riportando sui disegni [12].
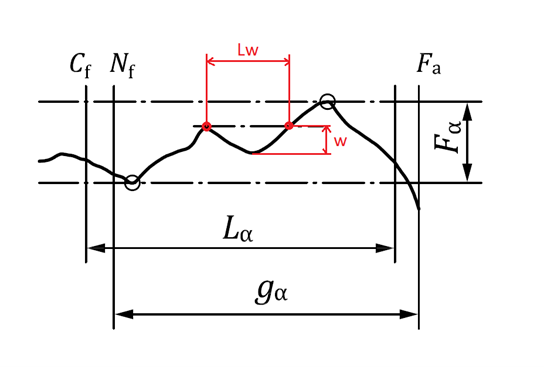
Una possibile definizione di waviness è la distanza fra due picchi sul profilo misurato in direzione perpendicolare all’evolvente, solo per i picchi che distano fra loro almeno il 20% della lunghezza del segmento di azione (Lw > 0.2 gα). L’ondulazione massima potrebbe essere definita anche da una frazione dell’errore di profilo ffα. Non ci sono comunque normative ISO di riferimento per questo valore. [13].
In questo caso il closed loop consiste nel valutare l’effetto della waviness rilevata sull’errore di trasmissione.
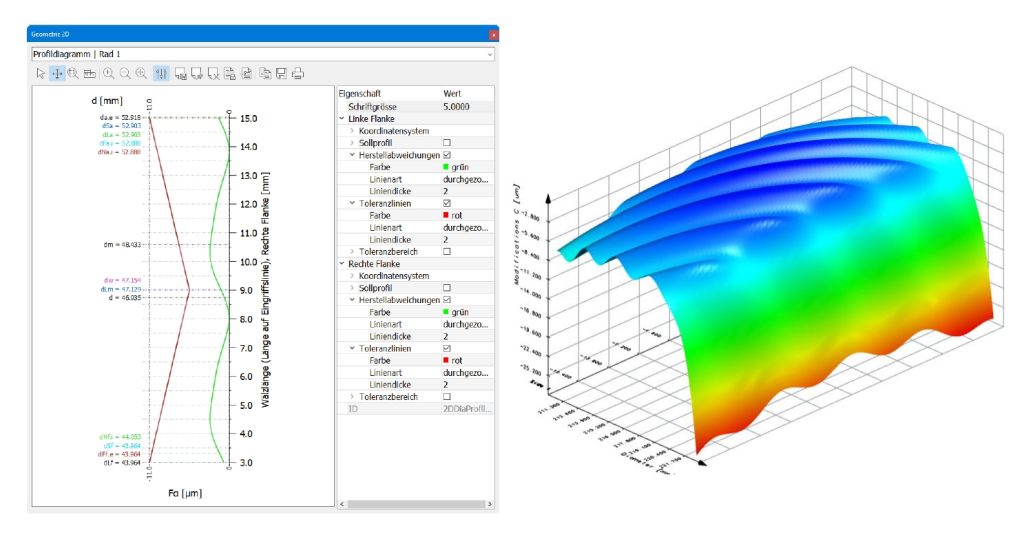
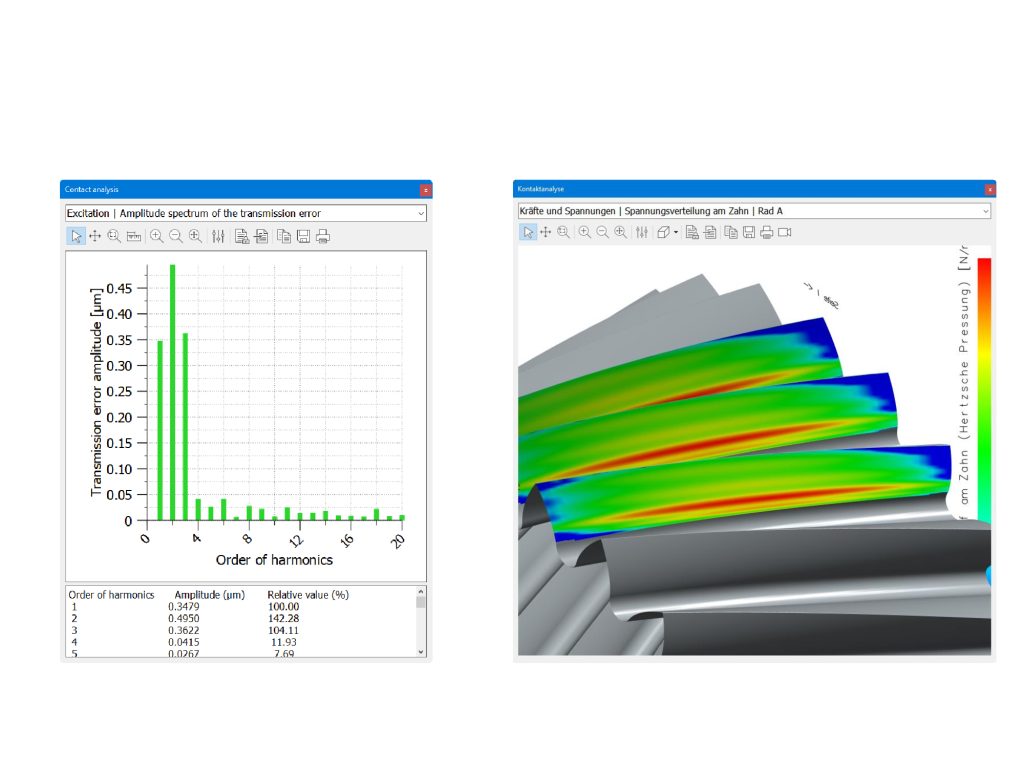
Il profilo misurato è stato esportato dalla GMM (evolventimetro) e importato nel software di progettazione e analisi (figura 11). Gli effetti della waviness sono stati quantificati con un’analisi di contatto sotto carico (figura 12).
Questo tipo di analisi può essere effettuata considerando un singolo dente o ciascun dente della ruota, grazia al cosiddetto ”fast GMM” [14] e a software di analisi del contatto che possono processare una particolare microgeometria per ciascun dente [11].
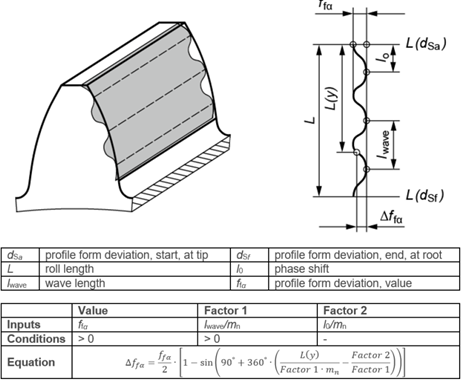
Prima di prendere in considerazione il rilievo del profilo fatto da una GMM, ci può simulare la waviness con una formulazione analitica della modifica del profilo ffa (figura 13).
Corone per viti senza fine
Per i riduttori a vite senza fine, spesso il disegno (la specifica) manca di un’informazione precisa sulla bombatura della corona e quindi sull’impronta di contatto sotto carico.
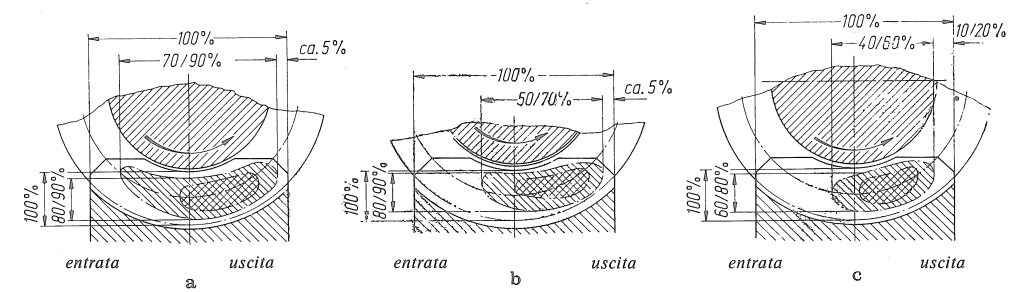
Suggerimenti su come dovrebbe essere questa impronta si trovano in [15], come riportato in figura 14.
In genere la bombatura è ottenuta maggiorando il diametro esterno del creatore rispetto alle dimensioni della vite [16] [17] e posizionandolo inclinato rispetto all’asse della vite, a un interasse ovviamente maggiorato.
A differenza delle ruote cilindriche, le cui modifiche di microgeometria sono di solito ottenute in rettifica, con mole appositamente profilabili, le corone delle viti senza fine, in bronzo o ghisa, sono finite di creatore. In questo caso l’affilatura dell’utensile, modifica l’impronta di contatto delle corone per viti senza fine.
Affinché siano soddisfatti i requisiti di ingranamento devono essere almeno rispettate le condizioni delle equazioini 1,2e 3, [18]:

dove
dm1 è il diametro medio della vite
Ym1 è l’angolo di inclinazione della vite
d’m0 è il diametro medio del creatore maggiorato
Y’0 è l’angolo di inclinazione del creatore maggiorato
d”m0 è il diametro medio del creatore dopo affilatura
Y”0 è l’angolo di inclinazione del creatore dopo affilatura
η è l’angolo di posizionamento del creatore sulla macchina utensile
Recentemente alcune aziende hanno adottato il closed loop per le corone delle viti senza fine seguendo questi passi:
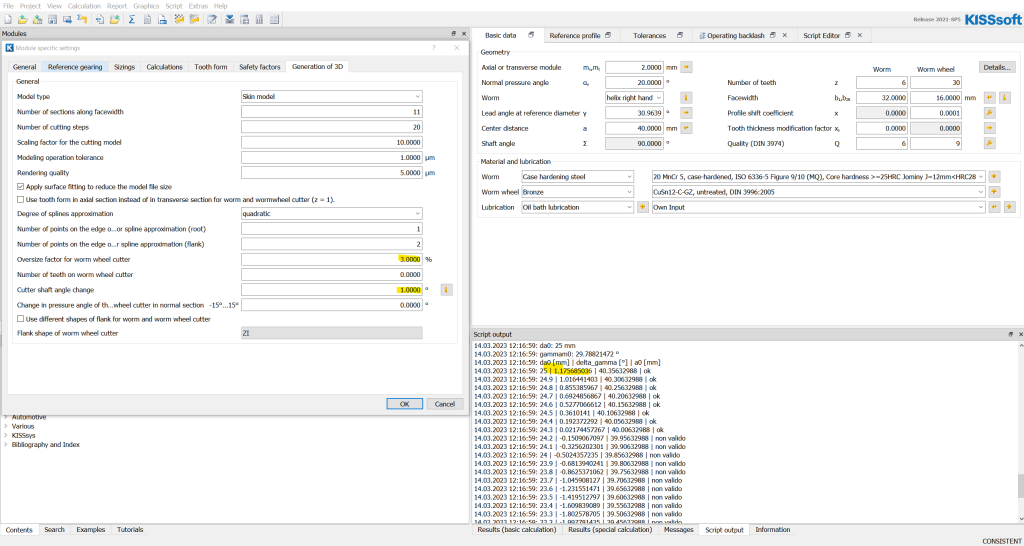
- progettazione della coppia vite corona prevedendo una maggiorazione del creatore della corona (figura 15);
- verifica numerica e grafica dell’impronta di contatto (figura16);
- generazione della tabella “diametro esterno creatore | angolo di posizionamento creatore | interasse di taglio” tenendo conto che il diametro esterno del creatore cala con le affilature (tabella 2);
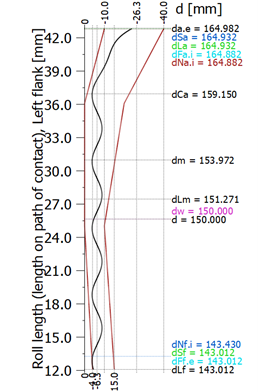
- esportazione della griglia per GMM senza tener conto della maggiorazione del creatore (master digitale), (figura 17);
- taglio secondo i parametri tabellati;
- rilievo su GMM e confronto con il master digitale (figura 18).
| da0 [mm] | η [°] | a [mm] | Usability |
| 24.887 | 0.996396079 | 40.30 | ✓ |
| 24.787 | 0.835111711 | 40.25 | ✓ |
| 24.687 | 0.671978307 | 40.20 | ✓ |
| 24.587 | 0.506961855 | 40.15 | ✓ |
| 24.487 | 0.340027451 | 40.10 | ✓ |
| 24.387 | 0.171139267 | 40.05 | ✓ |
| 24.287 | 0.000260518 | 40.00 | ✓ |
| 24.187 | -0.172646576 | 39.95 | ✗ |

Il primo risultato da controllare nel report della GMM è lo spessore del dente (cordale in sezione frontale): perché permette di tenere sotto controllo il gioco di ingranamento. Prima dell’adozione di questa procedura, il gioco di ingranamento veniva verificava con l’ingranometro a fianco singolo.
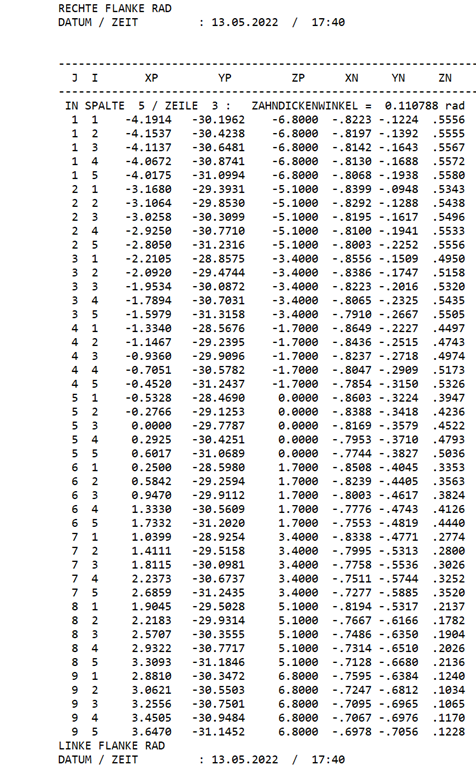
Il grafico di figura 18b mostrerà una bombatura fino a quando l’utensile non giunge a fine vita. La bombatura scomparirà quando l’utensile assumerà le dimensioni della vite.
L’operatore dispone in officina dello stesso software usato in progettazione e può generare la griglia (master digitale) che tenga conto delle dimensioni effettive del creatore che ha tagliato la corona che sta misurando. In questo caso il grafico non mostrerà la bombatura ma solo gli errori.

Conclusioni
Il closed-loop è un miglioramento del processo di realizzazione delle ruote dentate che collega in maniera bidirezionale la progettazione e la produzione. Condizione necessaria perché si possa adottare è la consapevolezza che specifica e verifica devono anch’esse essere collegate: non si può richiedere ciò che non è possibile misurare. Il processo di misura deve essere definito in maniera univoca così come lo sono già le grandezze da misurare.
Ringraziamenti
Gli Autori desiderano ringraziare prima di tutto KISSsoft e Gleason per i loro software. Un ringraziamento speciale va a Bonfiglioli, Comer, CNH, Gildemeister, Stellantis e Varvel – Mechnology che hanno adottato il closed loop descritto in questo articolo.
Bibliografia
[1] Kagermann, H., Lukas, W.-D., and Wahlster, W., 2011, “Industrie 4.0: Mit dem Internet der Dinge auf dem Weg zur 4. industriellen Revolution – ingenieur.de”, ingenieur.de – Jobbörse und Nachrichtenportal für Ingenieure [Online]. Available: https://www.ingenieur.de/technik/fachbereiche/produktion/industrie-40-mit-internet-dinge-weg-4-industriellen-revolution/. [Accessed: 13-May-2022].
[2] ISO 1:2016, Geometrical Product Specifications (GPS) — Standard Reference Temperature for the Specification of Geometrical and Dimensional Properties.
[3] Deni, M., 2013, “Gear Standards and ISO GPS”, GEAR TECHNOLOGY, pp. 54–57.
[4] Turci, M., 2021, “Integrated Optimization of Gear Design and Manufacturing”, Fall Technical Meeting (FTM), AGMA, Chicago.
[5] Brown, J., 2000, “Closed-Loop Gear Manufacturing System Speeds Design to Manufacturing”, Machine Design.
[6] Brumm, M., 2018, “Closed Loop Machining of Cylindrical Gears”, Gear Solutions.
[7] 2021, “GEMS – Gleason Engineering and Manufacturing System”.
[8] Plato, Apology.
[9] Shigley, J. E., and Mischke, C. R., eds., 1996, Standard Handbook of Machine Design, McGraw-Hill, New York.
[10] Kissling, U., Stolz, U., and Turich, A., 2019, “Combining Gear Design with Manufacturing Process Decisions”, pp. 1533–1544.
[11] “KISSsoft Calculation Program”.
[12] Frazer, R. C., Koulin, G., Reavie, T., Wilson, S. J., Zhang, J., and Shaw, B. A., 201AD, “The Application of Geometrical Product Specification (GPS) – Compatible Strategies for Measurement of Involute Gears”, Gear Technology, pp. 73–78.
[13] VDI/VDE 2612-1:2018, 2018, Measurement and Testing of Gears.
[14] Türich, A., 2022, “Gear Hard Finishing with up to 100% In-Process Inspection”, VDI-Berichte Nr. 2389, 2022, VDI Verlag GmbH, Düsseldorf.
[15] Niemann, G., and Winter, H., 1986, Elementi di Macchine vol. 3, Edizioni di scienza e tecnica ; Springer, Milano; Berlin.
[16] Kohara Gear Industry, Gear Technical Reference.
[17] Crosher, W. P., 2002, Design and Application of the Worm Gear, ASME Press, New York.
[18] Dudás, I., 2000, The Theory and Practice of Worm Gear Drives, Penton Press, London.
Articolo tratto da una relazione presentata all’AGMA FTM 2022 e stampato con l’autorizzazione dell’American Gear Manufacturers Association, proprietaria dei diritti d’autore. American Gear Manufacturers Association, 1001 N. Fairfax Street, 5th Floor, Alexandria, Virginia 22314. Le dichiarazioni e le opinioni espresse in questo testo sono quelle degli autori e non sono da considerarsi ufficiali dell’American Gear Manufacturers Association. Si ringrazia l’AGMA per la gentile autorizzazione alla pubblicazione (NdR).
Massimiliano Turci, Studio Tecnico Turci
Vincenzo Solimine





