Viene presentata la progettazione di un riduttore epicicloidale innovativo per veicoli elettrici ad alte prestazioni. Si mostrano: le principali caratteristiche degli ingranaggi; il metodo usato per il dimensionamento delle dentature; l’innovazione introdotta per facilitare il montaggio dei componenti del riduttore
Gli ingranaggi sono uno degli elementi chiave delle trasmissioni meccaniche e i loro parametri di utilizzo, come carichi e velocità di funzionamento, possono variare notevolmente in diverse applicazioni. L’enorme diffusione di questi organi meccanici ha indotto, nel corso degli anni, un progressivo sviluppo di norme standardizzate che forniscono linee guida nella progettazione e produzione di ingranaggi. Una delle applicazioni più comuni della trasmissione di potenza è quella dei riduttori di velocità. In particolare, nelle automobili è necessario trasmettere la potenza dal motore alle ruote motrici. I riduttori moltiplicano la coppia alle ruote, garantendo così la trazione del veicolo. Esistono diverse tipologie di riduttori, tra cui quelli ad assi paralleli e quelli epicicloidali. In questo progetto è stata sviluppata quest’ultima soluzione, migliore dal punto di vista delle performance per veicoli elettrici ad alte prestazioni. In questo caso, infatti, sono richiesti alti rapporti di riduzione e minimi ingombri, caratteristiche tipiche dai riduttori epicicloidali. Questa tesi è stata sviluppata all’interno dell’azienda CIMA S.p.A., nell’ambito di un progetto di tirocinio.
I riduttori epicicloidali
I riduttori epicicloidali sono composti da una ruota solare, una corona dentata, uno o più satelliti e un portasatelliti. La ruota solare, che è anche motrice, è collegata direttamente al motore elettrico del veicolo. In questo progetto, la ruota solare ha una velocità di rotazione massima pari a 13600 rpm, che è la velocità massima del motore elettrico. Nella prassi, si usano generalmente tre o quattro satelliti: aumentarne il numero permette di ripartire le forze trasmesse su più denti, con conseguente diminuzione delle sollecitazioni su ciascuna ruota. D’altro canto, questo porta anche a maggiori disuguaglianze di ripartizione dei carichi. Ciò è dovuto a inevitabili difformità di fabbricazione e/o di montaggio, che portano uno dei satelliti a subire maggiori sollecitazioni rispetto agli altri. Nella progettazione, si considera questo effetto con il coefficiente correttivo KY maggiorando la forza sul dente durante il funzionamento. Un’ulteriore considerazione riguarda il montaggio dei satelliti, che deve essere simmetrico attorno alla ruota solare. Ciò è richiesto per bilanciare le forze radiali tra gli n ingranamenti, le quali si annullano vicendevolmente anziché scaricarsi sul portasatelliti. Tale condizione è equivalente a:
z1 – z3 = n × m (1)
con z1 = numero di denti del solare, z3 = numero di denti della corona (negativo, perché è una ruota interna), n = numero di satelliti, m = numero intero qualsiasi. Un’ulteriore verifica è sul numero massimo di satelliti, per poterli montare evitando interferenza tra gli stessi. Si ha che
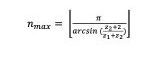
(2)
con: [x] = massimo numero intero inferiore a x e z2 = numero di denti dei satelliti. Nel funzionamento, i satelliti ingranano, oltre che con la ruota solare, anche con la corona dentata, che è fissa al telaio.
Dati di progetto
Dal catalogo Pirelli, fornitore di pneumatici per veicoli stradali ad alte prestazioni, si sono confrontate cinque configurazioni, relative a differenti dimensioni dei cerchi del veicolo: R18, R19, R20, R21 e R22. I due motori elettrici (identici) per la trazione del veicolo sono stati scelti a priori come dato di progettazione, con le caratteristiche riassunte in tabella 1.
| Potenza massima | 556kW (2 x 278 kW) |
| Coppia massima | 1120 Nm (2 x 560 Nm) |
| Velocità massima | 13600 rpm |
Un altro dato fissato all’inizio è la massa totale dei riduttori, che è al massimo di 54 kg (2 x 27 kg), esclusi motori e inverter. I parametri geometrici di riferimento per la dentatura sono mostrati in tabella 2.
| Modulo normale mn | 1,80 mm – 2,20 mm |
| Angolo di pressione a | 17,5° – 22,5° |
| Angolo d’elica β | 15° – 25° |
Per questi parametri sono stati forniti degli intervalli di valori ammissibili. Procedendo per tentativi, si è arrivati alla soluzione ottimale all’interno di questi limiti. Un ulteriore dato da considerare è il ciclo di carico del veicolo. I carichi a cui è sottoposto il riduttore di un veicolo ad alte prestazioni sono riportati in tabella 3, che mostra la potenza e il numero di giri del motore. Tali valori sono assunti per una certa percentuale di funzionamento rispetto alla vita utile del veicolo e sono stati presi in base all’esperienza aziendale. Ad esempio, il veicolo è sottoposto a metà dello sforzo massimo per il 30% della propria vita (fattore potenza = potenza effettiva/potenza massima = 0,5), considerando che si tratta di una vettura sportiva e che potrà essere sfruttata anche in pista. Per un altro 30% della vita utile la potenza utilizzata è il 50% della potenza massima e per il restante 30% della vita è il 25%. Tali valori sono stati inseriti in un programma di calcolo per verificare la resistenza a fatica tenendo conto dei danni cumulati per ogni ciclo di carico.
| Frequenza [%] | Fattore potenza | Potenza [kW] | Numero di giri [rpm] | Momento torcente [Nm] |
| 40 | 1 | 278 | 4740,5 | 560 |
| 30 | 0,5 | 139 | 4740,5 | 280 |
| 30 | 0,25 | 69,5 | 4740,5 | 140 |
Normative di riferimento
La progettazione delle ruote dentate segue le norme internazionali sulla capacità di carico degli ingranaggi, raccolte nella ISO 6336 del 2019: queste indicano i calcoli necessari per dimensionare correttamente un ingranaggio per l’applicazione richiesta. Il primo documento della norma presenta i principi di base e i fattori generali di influenza per il calcolo della capacità di carico di ingranaggi cilindrici ed elicoidali. Insieme agli altri documenti della serie ISO 6336, fornisce diversi metodi di progettazione per ruote dentate, ognuno con il proprio livello di affidabilità. Tali metodi sono stati validati per le seguenti condizioni: angolo di pressione normale an tra 15° e 25°, angolo d’elica b fino a 30°, grado di ricoprimento trasversale et tra 1 e 2,5. Inoltre, vengono fornite formule per il calcolo della capacità di carico in funzione delle diverse modalità di cedimento, come la rottura a piede dente, il pitting, la frattura dei fianchi, il grippaggio, il micropitting, etc. Nel calcolo delle tensioni di lavoro vengono introdotti dei coefficienti correttivi, che tengono in considerazione una grande quantità di parametri, relativi alla geometria e alle condizioni di funzionamento.
Primo dimensionamento di massima
La progettazione del riduttore epicicloidale è stata fatta usando un programma di calcolo all’avanguardia, KISSsoft, che applica le principali norme per il dimensionamento delle ruote dentate. Per la prima fase del progetto, ovvero il dimensionamento di primo tentativo del riduttore, è stato usato Excel, in cui sono stati sviluppati cinque fogli di calcolo, uno per ciascuna dimensione dei cerchi delle ruote del veicolo. In ogni foglio, dopo aver inserito i dati di partenza, sono state calcolate le dimensioni degli ingranaggi e il rispettivo numero di denti. Per fare ciò sono stati assunti valori di modulo e di angolo d’elica pari, rispettivamente, a 2 mm e 20° (valori medi dei range di ammissibilità). Si è poi ricavato il rapporto di riduzione tra la velocità del motore e la velocità delle ruote. Dopo vari tentativi per la scelta del numero di denti, partendo dai valori di riferimento dei clienti di CIMA S.p.A., si è arrivati alla soluzione ottimale per tutte le configurazioni di cerchi:
z1 0 23, z2 = 45, z3 = – 112
dove il segno meno per l’ultimo valore indica che la ruota 3 è a dentatura interna. Questi valori soddisfano la condizione di simmetria per 3 satelliti dall’Equazione (1):
z1 – z3 = n × m; il rapporto di riduzione tra motore e ruote (tenendo conto delle diverse dimensioni dei cerchi e della velocità massima richiesta di 320 km/h) è compreso tra 5,72 e 6,04. Di conseguenza, anche la velocità massima raggiungibile dal veicolo dipende dalle dimensioni dei cerchi, ma comunque con una variazione rispetto al valore richiesto inferiore al 6%. In questo primo tentativo, come in tabella 3 e considerando il massimo carico applicato, ovvero per una potenza di picco pari a 278 kW e una coppia massima di 560 Nm; la velocità della ruota solare è 4740,5 rpm.
Ottimizzazione in KISSsoft
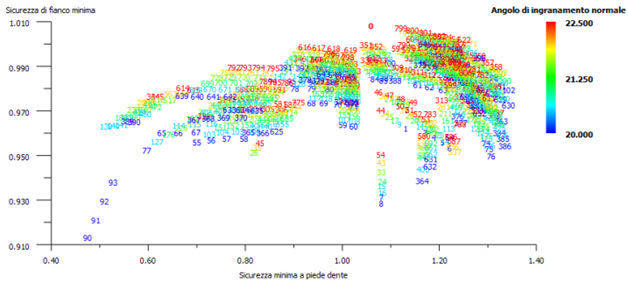
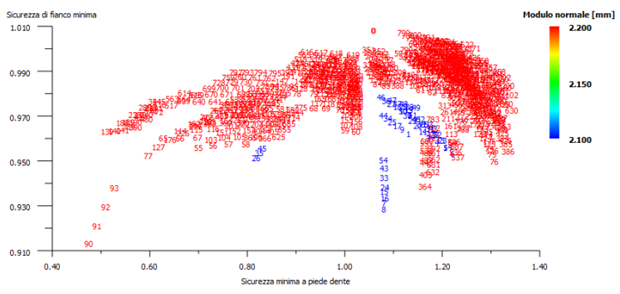
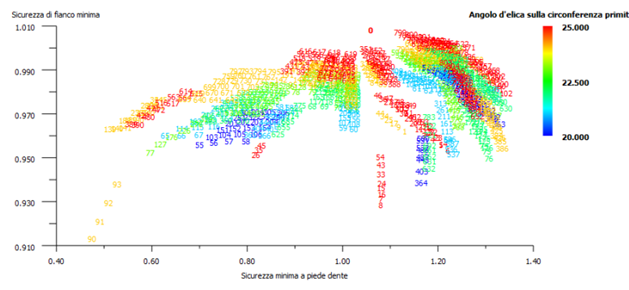
Il software di progettazione permette di ottimizzare i valori di modulo, angolo di pressione, interasse, larghezza di fascia, fattori di spostamento, angolo d’elica etc., per ottenere un rotismo a regola d’arte. In questo progetto si è usata l’ottimizzazione proposta dal programma, alla voce “progettazione di precisione macrogeometria”, procedendo per prove ed errori. L’ottimizzazione suggerita da KISSsoft calcola una grande quantità di dimensionamenti con i relativi coefficienti di sicurezza. Sono stati presi come obiettivi i coefficienti di sicurezza a flessione (del piede del dente) e a pitting (del fianco). Per ogni parametro geometrico si ricavano dei grafici che mostrano i coefficienti di sicurezza ottenuti in funzione di quello specifico parametro. Il grafico relativo all’angolo di pressione α (figura 1) mostra che i valori di sicurezza più elevati (in alto a destra) si hanno per α = 22,5°. Lo stesso ragionamento è stato fatto per l’angolo d’elica β, preso pari a 25° (figura 3) e per il modulo m, pari a 2,2 (figura 2).
Il materiale utilizzato per la ruota solare, satelliti e corona è un acciaio da cementazione, il 18CrNiMo7-6 con qualità secondo la norma ISO 6336-5, cementato e con durezza a cuore ≥ 25 HRC e in superficie pari a 61 HRC. Si è deciso di rettificare i denti della ruota solare e dei satelliti, ma non della corona, che, avendo un numero di denti maggiore, con spessore maggiorato alla base e un profilo di forma concava (anziché convessa), è più resistente. Per la correzione ?, ci sono varie ottimizzazioni possibili che possono guidare la scelta.
Nel riduttore in esame, si è deciso il valore di ? per le tre ruote parallelamente alla scelta dell’interasse. Note le dimensioni di partenza delle ruote, date da modulo e numero di denti, il range dell’interasse è 82,0 – 84,0 mm. Proseguendo per step successivi, a partire da 82 mm e con incrementi di 0,2 mm, si è arrivati al valore di 83,0 mm, che ottimizza i coefficienti di sicurezza a pitting e a flessione del dente. Dopo queste considerazioni, si sono assunti i fattori di correzione in tabella , per minimizzare gli strisciamenti specifici e dunque l’usura dei denti.
| Solare | Satelliti | Corona | |
| Fattori di correzione x | 0,2053 | 0,0100 | -0,8100 |
Una sezione del software molto utile per la progettazione è relativa alle modifiche della microgeometria. In particolare, sono state implementate tre tipologie di modifiche, riassunte in tabella 5. Modificare la microgeometria permette di migliorare la resistenza a pitting e a fatica flessionale. Si è deciso di intervenire solo sui satelliti, date le difficoltà di lavorazione su componenti interni, come la corona, e sulla ruota solare, ricavata di pezzo sull’albero. Le tre modifiche effettuate sono state scelte grazie all’esperienza dell’azienda. L’entità delle modifiche è dell’ordine del μm: queste possono sembrare irrilevanti, ma nella pratica risultano assai utili per ottimizzare il funzionamento degli ingranaggi, specialmente quando questi trasmettono carichi notevoli con deformazioni non trascurabili.
| Bombatura longitudinale sull’elica | 15 mm | |
| Bombatura del profilo, centrata sull’evolvente | 4 mm | |
| Spoglia di testa lineare | Lca = 80 mm Caa = 1,1 m (m 0 modulo) |
Nuovo montaggio brevettato
Nello svolgimento del progetto si è sviluppata una nuova modalità di montaggio dei componenti per l’accoppiamento tra satelliti e portasatelliti. In particolare, il progetto di partenza (figura 4) adottava una coppia di cuscinetti a rulli (1), montati in configurazione ad “O” (o back-to-back) sui perni cavi (2) inseriti nei satelliti (3). Tali perni, che sono fissati in appositi alloggiamenti (4) sul portasatelliti, permettono la rotazione relativa tra quest’ultimo e i satelliti, e dunque la corretta trasmissione di potenza.
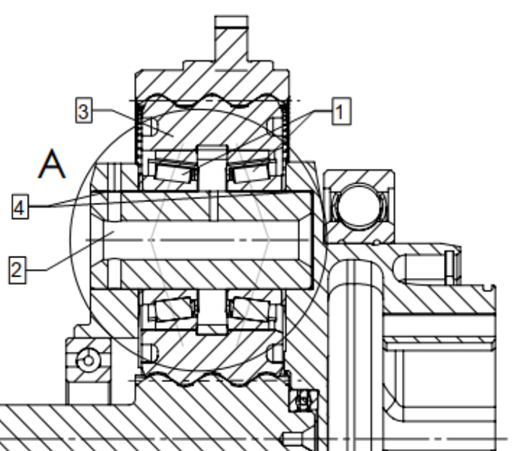
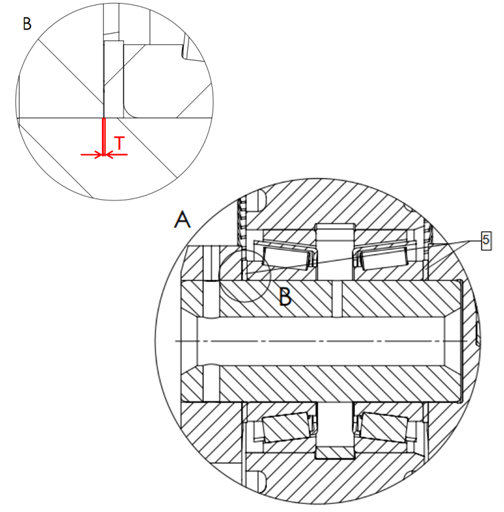
Come mostrato in figura 5, il gioco assiale (T) dei cuscinetti deve essere in un range di tolleranza. Tale gioco, nella configurazione classica, viene regolato mediante rondelle o distanziali pelabili (5), ovvero componenti formati da sottili lamine metalliche sovrapposte che permettono una regolazione dell’ordine del centesimo di millimetro. La regolazione, però, deve tenere conto delle dimensioni assiali e delle relative tolleranze dei cuscinetti e degli spallamenti interni dei satelliti. Di conseguenza, le operazioni di regolazione possono essere lunghe e delicate, sia in fase di montaggio che di manutenzione. Inoltre, la misura delle quote e la modifica dello spessore delle rondelle necessita lo smontaggio del perno e dei cuscinetti dagli alloggiamenti del portasatelliti. Tale operazione è pertanto lenta e deve essere realizzata da operai specializzati per ogni riduttore.
L’innovazione di questo progetto, per la quale è stata depositata una domanda di brevetto, è mostrata in figura 6 e consiste nell’adozione di un perno filettato (6), accoppiato con una madrevite (7) ricavata nel portasatelliti. La regolazione del gioco assiale tra perno e cuscinetto è allora realizzata mediante avvitamento e svitamento del perno stesso.
È prevista una cava esagonale (8) sulla testa del perno, visibile in figura 6, che si può stringere con una normale chiave a brugola. Noto il passo della filettatura e il gioco assiale (T) richiesto tra la testa del perno e l’anello (9) a battuta sul cuscinetto, la regolazione dell’accoppiamento è immediata. Inoltre, è previsto un organo di bloccaggio che, impegnando il perno, ne blocca il movimento assiale durante il funzionamento. Tale organo di sicurezza consiste in un grano filettato in rame (10), facilmente deformabile quando viene compresso sulla filettatura del perno. Anche il grano ha una cava esagonale, per essere avvitato nella madrevite (11) ricavata sul portasatelliti.
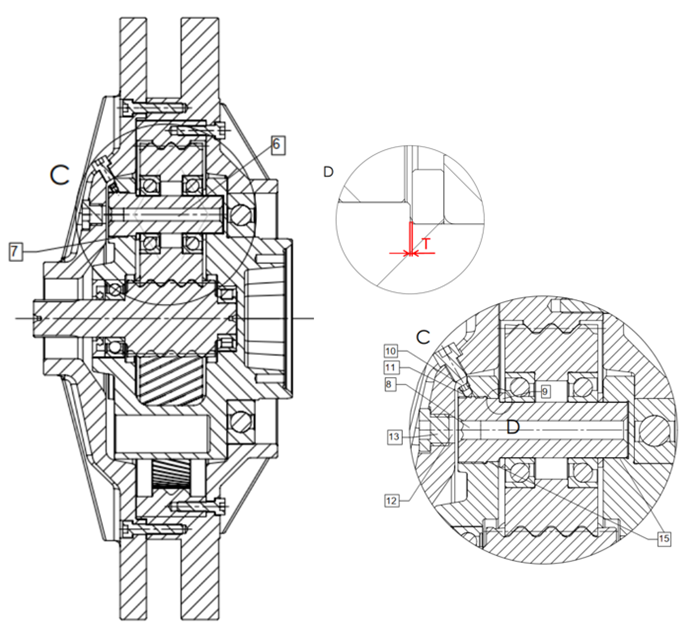
Un ulteriore vantaggio di questa concezione consiste nella facilità di regolazione del gioco in fase di manutenzione del riduttore. Infatti, l’accesso al perno e al grano è dato da un’apposita apertura (12) sulla scatola, accessibile svitando un tappo di protezione (13) e ruotando poi di 120° la posizione del portasatelliti per regolare il perno successivo (che diventa coassiale all’apertura nella scatola). La regolazione del gioco è così possibile anche con il riduttore installato a bordo veicolo, senza dover smontare gli ingranaggi dalla scatola e questa dal telaio. Il risparmio in termini di tempo e costi è dunque evidente. Inoltre, è possibile recuperare eventuali tolleranze ed errori di lavorazione mediante il semplice avvitamento del perno filettato. Si possono poi inserire rondelle commerciali di spessore noto, senza eseguire altre operazioni di regolazione. Il riduttore è così più economico e veloce da applicare, mantenendo elevati standard di qualità e sicurezza.
Bibliografia
[1] KISSsoft AG, “Manuale utente”, 2023.
Lorenzo Cotelli, CIMA spa
Giovanni Mottola, Dipartimento di Informatica, Bioingegneria, Robotica e Ingegneria dei Sistemi – DIBRIS
Università di Genova


