Il metodo degli Elementi Finiti, o FEM, acronimo dell’espressione inglese Finite Element Method, è largamente utilizzato nell’ambito della progettazione meccanica per approcciare i problemi di calcolo strutturale, con l’obbiettivo di calcolare gli sforzi e le deformazioni prodotti nei componenti delle macchine dai carichi ai quali sono sottoposti in esercizio.
Sebbene questa sia la prima applicazione nel quale il metodo ha trovato impiego, esso costituisce un approccio più generale per la soluzione numerica approssimata dei problemi dei continui, nei quali si deve calcolare una grandezza di campo, cioè per quei problemi, tipicamente governati da equazioni differenziali, le cui incognite sono equazioni che descrivono l’andamento di una grandezza variabile con continuità. Quindi, oltre che per la “stress analysis”, elastica o non elastica, alla quale si farà qui prevalentemente riferimento, possono essere applicati anche ad esempio a problemi di scambio termico o di moto dei fluidi o di magnetismo, solo per citarne alcuni.
Un po’ di storia
Gli albori del metodo risalgono agli anni quaranta del secolo scorso e sono quindi precedenti all’avvento dei calcolatori elettronici, ma è solo grazie a questi ultimi che esso è divenuto uno strumento utilizzabile in modo proficuo per risolvere problemi di utilità pratica. Il termine Elementi Finiti apparve per la prima volta negli anni sessanta.
Negli anni settanta iniziarono a diffondersi i primi software, che oggi sono presenti in gran numero e sono comunemente utilizzati per risolvere problemi anche molto complessi, grazie alla disponibilità di sistemi di calcolo elettronico sempre più performanti.
Risolvere i problemi con il FEM
Nonostante la larga diffusione e la facile accessibilità degli strumenti di calcolo è però indispensabile che il calcolo ad elementi finiti sia utilizzato in modo responsabile, senza cioè prescindere dalle indispensabili conoscenze teoriche sia del tipo di problema che si deve risolvere, sia dell’approccio matematico sottostante. Nel caso dei problemi strutturali, l’analista deve in particolare conoscere approfonditamente la cinematica e la statica delle strutture oltre che la natura delle approssimazioni introdotte utilizzando il metodo degli elementi finiti.
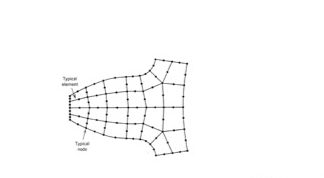
Nel FEM, il continuo viene suddiviso in un numero finito di elementi, connessi tra di loro in corrispondenza dei nodi, generando la cosiddetta mesh: l’andamento della funzione incognita, che nel caso strutturale è in primo luogo lo spostamento, viene approssimato interpolando i valori in corrispondenza dei nodi mediante polinomi (individuati dalle funzioni di forma) e le equazioni differenziali che governano il problema vengono così trasformate in un sistema di equazioni algebriche, che rappresentano la condizione di equilibrio in corrispondenza dei nodi stessi (figura 1).
KD = R
Il sistema viene generalmente rappresentato in forma matriciale, dove con D si identifica il vettore degli spostamenti nodali, con R quello dei carichi nodali e con K la matrice di rigidezza dell’intera struttura, ottenuta assemblando quella dei singoli elementi sulla base della connettività nodi/elementi.
Una volta risolto il sistema, noti cioè gli spostamenti ai nodi, è possibile esprimere l’andamento dello spostamento in ciascun elemento mediante le funzioni interpolanti e derivare quindi le altre grandezze di interesse, quali le deformazioni e gli sforzi. In generale la soluzione che si trova differisce da quella esatta ma ci si avvicina a questa riducendo la dimensione degli elementi, cioè aumentandone il numero, e/o aumentando l’ordine delle funzioni di forma polinomiali utilizzato per l’interpolazione.
Nonostante la realtà che ci circonda sia tridimensionale, anche nell’approccio numerico del FEM, così come avviene per quelli analitici, è talvolta possibile sfruttare alcune prerogative della struttura e dei carichi applicati per semplificare il modello, utilizzando laddove sussistano le condizioni, elementi monodimensionali (travi o aste) o bidimensionali (piani, piastre, gusci) o elementi assialsimmetrici, come indicato nella tabella 1 che riassume le principali tipologie di problemi ed elementi utilizzabili. Ciò comporta una riduzione dell’ordine della geometria modellata, che diviene ad esempio monodimensionale nel caso dell’elemento trave, senza però perdere il comportamento legato alla tridimensionalità, che in questo caso viene garantito introducendo le informazioni relative alle proprietà geometriche della sezione nel modello matematico dell’elemento.
| Problema | Elemento | Geometria |
| Piano (2D) | asta e trave | 1D |
| sforzo piano | 2D | |
| deformazione piana | 2D | |
| 3D | asta e trave | 1D |
| solido | 3D | |
| piastra e guscio | 2D/3D | |
| Assialsimmetrico | assialsimmetrico trave | 1D |
| assialsimmetrico piano | 2D |
Il giusto compromesso
L’abilità dell’analista consiste nella capacità di trovare il giusto compromesso tra la bontà dell’approssimazione e le risorse di calcolo necessarie, utilizzando elementi adatti per tipologia e dimensioni, adeguando localmente la fittezza della suddivisione in relazione al gradiente delle grandezze da calcolare.
All’utente del metodo è quindi richiesta la conoscenza delle proprietà dei diversi tipi di elementi utilizzabili, delle relative funzioni di forma e delle conseguenti implicazioni sulle capacità dell’elemento di approssimare l’andamento delle grandezze incognite.
Considerando ad esempio gli elementi piani, il più semplice tra di essi è l’elemento triangolare a tre nodi, nel quale lo spostamento è descritto mediante funzioni lineari che, tenuto conto della relazione tra spostamenti, deformazioni e sforzi, rappresenta questi ultimi come costanti nell’elemento e per questo motivo è anche indicato con il nome di Constant Strain Triangle (CST): è del tutto evidente che esso non si presta allo studio di casi caratterizzati da elevata variabilità dello sforzo, se non al prezzo di mesh molto fitte, con conseguente aumento delle risorse di calcolo necessarie. Il passaggio agli elementi triangolari quadratici, con sei nodi (tre ai vertici e tre sui lati), consente di modellare deformazioni e sforzi lineari (e per questo è anche indicato come LST – Linear Strain Triangle).
Anche se apparentemente simile, il comportamento degli elementi quadrangolari è significativamente diverso: ad esempio l’elemento a quattro nodi, che interpola gli spostamenti con funzioni lineari, è in grado di descrivere la deformazione e lo sforzo nella direzione in una delle due coordinate cartesiane come funzioni lineari dell’altra ed è quindi in grado di cogliere la variabilità derivante ad esempio da una sollecitazione di tipo flessionale (figura 2).
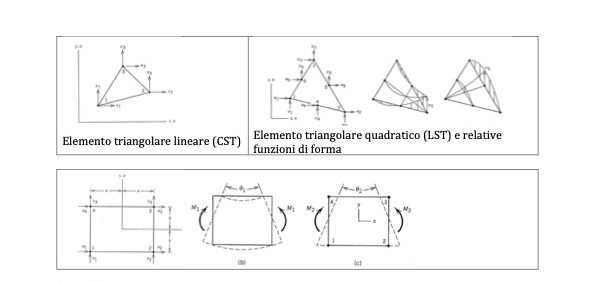
Il caso dell’elemento quadrangolare ci consente di descrivere un altro effetto del quale l’utente deve essere consapevole: le immagini di figura mostrano rispettivamente la corretta deformata di un elemento rettangolare sottoposto a pura flessione (b) e quella possibile con le funzioni di forma lineari (c). Quest’ultima dà origine a deformazioni angolari e a conseguenti sforzi di taglio, che nella realtà non dovrebbero essere presenti (detti pertanto spuri), i quali assorbono parte del lavoro dei carichi dando luogo ad un comportamento flessionalmente più rigido di quello reale.
Altri effetti sono legati all’utilizzo dell’integrazione numerica per il calcolo delle matrici di rigidezza degli elementi. L’approccio seguito è in genere quello della quadratura di Gauss, che prevede il calcolo dell’integrale sulla base della valutazione della funzione integranda in un numero finito di punti, detti punti di Gauss. Alla luce dell’ordine di interpolazione utilizzato e del numero di punti di integrazione considerati, può succedere che vi siano condizioni di carico che, pur deformando l’elemento, producono spostamenti nulli nei punti di integrazione e che quindi non vengono colti, dando così luogo a fenomeni di instabilità, cioè incapacità (totale o parziale) della matrice di rigidezza dell’elemento di opporsi a tali sollecitazioni.
L’utilizzo dei preprocessori, cioè di interfacce interattive molto efficaci che agevolano la definizione del modello e l’introduzione dei dati, talvolta rende poco visibile all’utente la scelta di alcune opzioni che possono avere un impatto enorme sulla soluzione come ad esempio, riferendosi a quanto affermato poc’anzi, la scelta dello schema di integrazione, che può essere ridotto o normale.
Anche la fase di visualizzazione dei risultati non è esente da trappole, perché tipicamente presenta i risultati mediante trend regolari descritti con codici di colore variabili con continuità: si tratta però di andamenti ottenuti mediante interpolazioni e medie pesate di valori puntuali, che talvolta possono impedire di cogliere i corretti valori locali, o i gradienti, e l’analista esperto dovrebbe avere la capacità di scegliere l’opzione di visualizzazione più opportuna o addirittura di capire quando sia invece indispensabile accedere al risultato grezzo.
In questa breve esposizione, che non ha la finalità di presentare in modo organico il metodo degli elementi finiti, ho voluto sottolineare l’importanza della fruizione responsabile di uno strumento di calcolo di per sè potentissimo, che può però esporre l’utente ad amare sorprese se utilizzato senza le dovute competenze. Per una trattazione sistematica e per ulteriori approfondimenti su queste tematiche si rimanda a [1].
[1] R. D. Cook, “Finite Element Modeling for Stress Analysis”, John Wiley & Sons, Inc.


