L’attrito rappresenta da sempre uno dei maggiori problemi da fronteggiare per ottenere sistemi di posizionamento precisi e affidabili. L’uso di compensatori di attrito rappresenta una delle tecniche più efficaci al fine di ridurre le limitazioni dovute a questo particolare fenomeno. L’articolo fornisce una panoramica sulle principali tipologie di compensatori di attrito esponendo quelli che sono i loro principali limiti e punti di forza.

I sistemi di posizionamento servo pneumatici rappresentano una tecnologia che consente di combinare la forza e la velocità della tecnologia pneumatica con la precisione dei sistemi servo-comandati, ottenendo così soluzioni efficienti ed affidabili. I sistemi servo penumatici sono infatti capaci di gestire con elevata precisione sia movimenti di tipo lineare che rotativo, risultando ideali per una vasta gamma di applicazioni nei settori dell’automazione, della robotica e della produzione industriale. Inoltre, i continui progressi in ambito sensoristico ed elettronico e la sempre più pressante richiesta di soluzioni a basso impatto ambientale stanno favorendo ulteriormente la loro diffusione.

Al momento, il maggiore ostacolo da fronteggiare è la compensazione dei fenomeni legati alle forze di attrito. Queste, a causa della loro natura stocastica e non lineare, possono compromettere significativamente la precisione, ripetibilità, stabilità ed efficienza del movimento controllato. L’attrito è un fenomeno dissipativo che si manifesta a seguito dell’interazione tra le superfici di due corpi in contatto e che da un punto di vista fisico può essere considerato come una forza che si oppone al moto relativo tra i corpi stessi. A seconda delle condizioni in cui le superfici interagiscono (carichi applicati, velocità relativa, temperatura, tipologia di materiali, condizioni di lubrificazione…) è possibile assistere ad una grande e diversificata varietà di fenomeni legati all’attrito.

Nel caso degli attuatori pneumatici è sempre presente un ingrassaggio, tipicamente a vita, degli elementi striscianti (guarnizioni, pattini e boccole di guida); questo per trasformare i contatti di attrito da “attrito secco” ad “attrito lubrificato” e ridurre le forze di attrito, ridurre i fenomeni di usura aumentando così la durata dei componenti.

Nel caso di contatti lubrificati la forza di attrito segue l’andamento tipico definito da Stribeck in cui si distinguono tipicamente tre zone: lubrificazione limite (boundary), a bassissime velocità relative in condizioni immediatamente successive al primo distacco, lubrificazione mista (mixed) con diminuzione della forza di attrito all’aumentare della velocità e lubrificazione fluida o idrodinamica (fluid film) con forza di attrito crescente all’aumentare della velocità relativa. In condizioni di lubrificazione limite le asperità superficiali sono in stretto contatto e sottoposte a deformazioni elasto-plastiche localizzate e si ha la formazione, per assorbimento chimico o fisico, di uno strato limite di lubrificante; in questa fase tale strato svolge un ruolo importante nella determinazione della forza di attrito. All’aumentare della velocità relativa si ha man mano la separazione delle creste fino a completa separazione e forza d’attrito determinata da condizioni di lubricazione idrodinamica.

Un aspetto molto studiato e complesso riguarda le condizioni immediatamente antecedenti e successive al primo distacco delle due superfici: la prima costituisce la cosiddetta zona dell’attrito statico o di “pre-sliding”, la seconda è rappresentata dalla “boundary condition” descritta sopra. Antecedentemente al primo distacco, le interazioni tra le asperità che costituiscono le superfici avvengono prevalentemente sotto forma di deformazioni elasto-plastiche e fenomeni di adesione; anche in presenza di interazioni adesive tra le asperità sono comunque possibili micro-spostamenti tra i corpi dovuti alle micro deformazioni delle creste a contatto (pre slittamento).

Superata questa fase, all’aumentare della velocità relativa, si entra nella zona della lubrificazione limite con moto relativo tra i corpi, in cui in cui l’attrito è determinato sia dalla rottura dei contatti adesivi tra le creste sia dallo scorrimento dello strato limite; le asperità appartenenti alle due superfici hanno sempre meno tempo per interagire elasto-plasticamente o tramite fenomeni adesivi e sono soggette ad un continuo processo di adesione e rottura. Questa breve e semplicistica descrizione dovrebbe già dare un’idea dell’imprevedibilità che caratterizza questa tipologia di fenomeni. I compensatori di attrito rappresentano la soluzione più efficace e diffusa al fine di ridurre le limitazioni legate a questo fenomeno.

Lo scopo di questo articolo è fornire una panoramica generale sulle principali tipologie di compensatori di attrito dettagliando quelli che sono i loro principali limiti e punti di forza.

Tipologia e classificazione di compensatori

I compensatori sono algoritmi utilizzati all’interno di servosistemi per predire il valore di una variabile al fine correggere il segnale di comando fornito dal controllore. La Figura 1 riporta lo schema a blocchi di un sistema di posizionamento servo pneumatico con compensatore di attrito.

Il controllore è normalmente alimentato con un segnale di errore e e dalla stima fornita dal compensatore di attrito f e fornisce come uscita il segnale di comando u in base all’algoritmo di controllo utilizzato. Il segnale di errore e viene calcolato come differenza tra un segnale di riferimento x_ref e il segnale x misurato dai sensori. Il compensatore di attrito fornisce la sua uscita f sulla base del valore di forza di attrito stimata. Normalmente i sistemi di posizionamento servo pneumatici usano come segnale di retroazione quello relativo alla posizione dell’oggetto da movimentare.

I compensatori di attrito possono essere divisi in due principali categorie [1]:

• Compensatori basati su modelli matematici, detti model-based
• Compensatori non basati su modelli matematici, detti model-free

I compensatori di tipo model-based compensano gli errori legati ai fenomeni di attrito sulla base di modelli matematici che possono avere complessità diversa a seconda delle esigenze. Solitamente aumentare la complessità del modello migliora la precisione del compensatore ma ne può compromette la semplicità di implementazione.

I compensatori di tipo model-free utilizzano solitamente reti neurali, intelligenza artificiale o logiche fuzzy per prevedere i valori delle forze di attrito e compensare i loro effetti.

La necessità di implementare compensatori di tipo model-free nasce dal fatto che, sebbene esistano modelli di attrito molto completi, i modelli presenti ad oggi risultano essere di tipo semi-empirico e non possono risultare applicabili se non a valle di un’identificazione sperimentale.

Recentemente questo tipo di limitazione è stata attenuata integrando i compensatori model-based con algoritmi adattativi basati su algoritmi genetici, machine learning o intelligenza artificiale. Questa miglioria consente di tenere conto delle possibili variazioni dei parametri relativi al modello di attrito utilizzato e detti parametri possono così essere tarati anche durante il funzionamento.

Modelli di attrito

La conoscenza dei modelli utilizzati all’interno dei compensatori di attrito è utile per comprendere quelle che sono le principali problematiche connesse al fenomeno fisico in relazione all’implementazione dell’algoritmo di compensazione. In generale è possibile classificare i modelli di attrito in modelli tipo statico e dinamico [2].

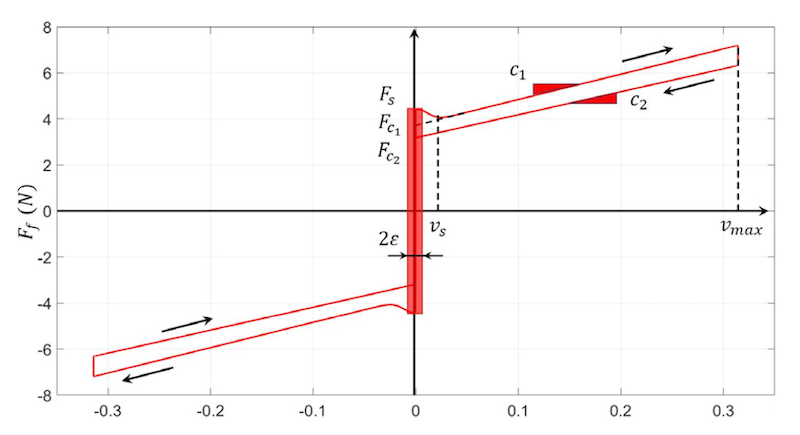
Le caratteristiche dei modelli di tipo statico possono essere rappresentate graficamente mediante una curva di Stribeck (vedi Figura 2).

Questa curva riporta i valori della forza di attrito F_f misurata al variare della velocità di strisciamento v e permette di visualizzare graficamente i parametri relativi ad un modello di attrito statico. Una volta superato il valore della forza di primo distacco F_s, all’aumentare della velocità di strisciamento, i valori della forza di attrito inizialmente si riducono per poi riaumentare e crescere in maniera lineare fino al raggiungimento del valore di velocità massima v_max. Questo tipo di andamento viene indicato come effetto Stribeck.

L’iniziale riduzione delle forze di attrito è legata al fatto che l’aumento della velocità di strisciamento riduce il tempo che le asperità delle superfici hanno per interagire tramite interazioni elastoplastiche e adesive. Successivamente, dopo aver raggiunto un minimo locale alla velocità v_s (detta velocità di Stribeck), la forza di attrito riaumentano all’aumentare della velocità a causa dell’energia dissipata a seguito degli impatti che avvengono tra le asperità.

Un altro fenomeno che si può notare osservando la curva di Stribeck riportata in Figura 2 è che in condizioni non stazionarie (velocità non costante), in fase di accelerazione il valore della forza di attrito risulta essere maggiore rispetto al caso di velocità stazionaria, mentre in fase di decelerazione si verifica il viceversa. Questo fenomeno si spiega con il fatto che la forza di attrito necessita di un certo tempo per “riadattarsi” alle nuove condizioni di velocità. L’equazione 1 [3] riporta il modello di attrito relativo alla curva di Stribeck riportata in Figura 2.

Le forze di attrito vengono considerate in maniera diversa a seconda che il corpo sia in moto o in quiete. La distinzione tra queste due condizioni viene definita mediante la tolleranza ε (corrispondente alla semi ampiezza della zona evidenziata in Figura 2). Quando la velocità v è in valore assoluto inferiore alla tolleranza, il corpo è considerato fermo.

Al contrario, quando il modulo della velocità è superiore alla tolleranza scelta, il corpo viene considerato in moto e la forza di attrito viene calcolata come somma di più termini. Il primo termine (sgn(v) F_C1) è relativo ad un modello di attrito coulombiano, il secondo (sgn(v)(F_S-F_C1 ) e^((-|v|/v_s )^δ )) descrive l’effetto Stribeck e il terzo (c_1 v) il contributo di attrito viscoso.

In caso di accelerazioni negative il termine legato all’effetto Stribeck non viene considerato. Sebbene questo sia il più completo modello statico di attrito presente in letteratura, questo non è sufficiente a descrivere tutti i fenomeni di attrito ad oggi noti. La necessità di considerare modelli di tipo dinamico nasce dal fatto che i modelli statici non forniscono alcuna informazione riguardo a quanto accade durante la fase che precede il primo distacco.

I modelli dinamici sono definiti tali in quanto considerano un’equazione ed una variabile di stato aggiuntiva per tenere conto dell’interazione che si ha tra le asperità delle superfici a contatto.

L’equazione 2 riporta la struttura standard condivisa dalla maggior parte dei modelli dinamici utilizzati ad oggi [4].

Dove, la prima equazione è l’equazione di stato che considera l’interazione tra le asperità delle superfici mediante un modello di spazzola equivalente. La variabile di stato z rappresenta la deformazione della spazzola equivalente. La seconda equazione permette di calcolare la forza di attrito F_f come somma di tre contributi. I primi due (σ_0 z(t)+σ_1 z ̇(t)) sono relativi alle forze elastiche e smorzanti dovute alle deformazioni della spazzola equivalente, mentre l’ultimo (cv(t)) tiene conto dell’attrito viscoso dovuto alla velocità del corpo in movimento.

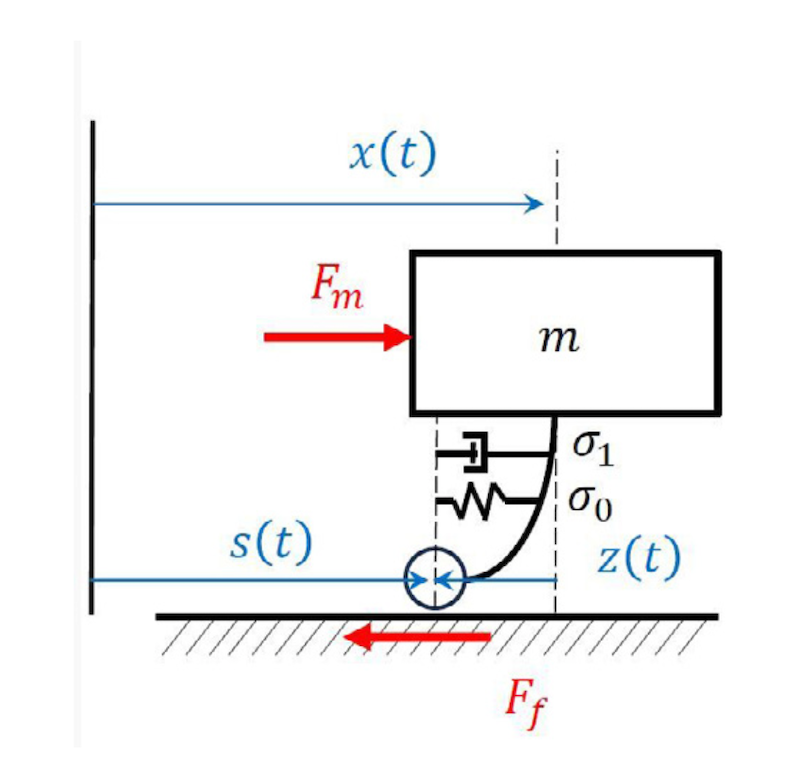
La Figura 3 riporta uno schema relativo al modello di spazzola equivalente, dove, x(t) corrisponde allo spostamento macroscopico del corpo in movimento (rappresentato dalla massa m), z(t) rappresenta la deformazione elastica della spazzola e s(t) è lo spostamento assoluto della spazzola. La struttura dell’equazione 3 è stata scelta in maniera tale da rispettare le seguenti condizioni:

In condizioni di aderenza, la deformazione elastica della spazzola z(t) aumenta, mentre lo spostamento assoluto della spazzola s(t) rimane costante.

In condizioni di strisciamento, lo spostamento assoluto della spazzola s(t) aumenta, mentre la deformazione della spazzola z(t) rimane costante e pari ad un valore stazionario z_ss

Le tipologie di modello dinamico si differenziano a seconda dell’espressione con cui si esprime il valore stazionario di deformazione della spazzola z_ss e l’espressione utilizzata per calcolare la forza di attrito F_f. Il valore stazionario di deformazione della spazzola z_ss viene espresso come la forza di attrito in condizioni di strisciamento F_ss divisa per la rigidezza σ_0 per unità di lunghezza della spazzola equivalente.

Ad esempio, nel caso del modello di LuGre che considera l’effetto Stribeck e forze di attrito di tipo coulombiano e viscoso:

L’unico effetto di cui non tiene conto questo modello è l’isteresi con memoria non locale di forma.

L’isteresi è un fenomeno complesso e spesso presente nel caso di movimenti ciclici o alternati. Esso è dovuto all’interazione di vari fattori, tra cui la dissipazione di energia, le proprietà dei materiali e la dinamica del sistema preso in esame.

La Figura 4 riporta alcune curve di esempio al fine di illustrare il fenomeno preso in esame. In particolare, le Figure 4a-b riportano gli andamenti temporali delle forze di attrito e degli spostamenti, mentre la Figura 4c la relativa curva forze-spostamenti. In generale, la forza di attrito tra due superfici non dipende solo dalla loro velocità relativa e dalle condizioni istantanee in cui le asperità superficiali si trovano ma anche dalle condizioni passate in cui le superfici si sono trovate.

Esaminando le curve è possibile notare come ad ogni inversione del moto il sistema “percorra” una nuova curva di transizione nel piano forza-spostamento. A seconda che il valore di spostamento registrato all’inversione sia maggiore o minore del valore massimo registrato fino a quel momento si può avere la chiusura o la creazione di un nuovo anello nel piano forze spostamenti.

Nell’esempio mostrato sono state riportate le corrispondenze tra le inversioni del moto (punti A, B, C, D, E, F) presenti nei vari istanti temporali e il numero di curve chiuse (AF, BC, DE) che si registrano sul grafico riportante la forza di attrito in funzione dello spostamento.

L’isteresi con memoria non locale può essere considerata solo attraverso modelli più complessi come il modello di Leuven, Leuven modificato e il modello di Maxwell o Maxwell generalizzato.

Struttura di un servo sistema con compensatore di attrito

Al fine di ridurre in maniera efficace gli effetti negativi dovuti all’attrito, si utilizzano servo sistemi che sfruttano la combinazione di un compensatore di attrito e un controllo retroazionato, come ad esempio, uno di tipo PID. I diagrammi a blocchi di Figura 5 mostrano le due principali soluzioni utilizzabili combinando controllore PID e compensatore di attrito. Se il compensatore viene inserito su un ramo parallelo e comunicante con il ramo diretto si parla di compensatore in anello aperto. Al contrario se il compensatore di attrito ha come ingresso il segnale retroazionato si parla di compensatore in anello chiuso.

Nel caso di compensatore in anello aperto (Figura 5a), il controllore PID serve ad assicurare la stabilità del sistema e la sua capacità di reiettare disturbi esterni, mentre il compensatore di attrito consente di migliorare la precisione nell’inseguire il segnale di riferimento. In questo caso, considerando la funzione di anello del sistema è possibile notare che al fine di ottenere un perfetto inseguimento del segnale di riferimento (r(t)=y(t)), la funzione di trasferimento del compensatore deve risultare pari all’inverso della funzione di trasferimento del sistema.

Il vantaggio di questa struttura è dovuto al fatto che il compensatore di attrito lavora tenendo conto del segnale di riferimento senza effettuare previsioni real-time del segnale di retroazione misurato. È importante sottolineare che in questi casi il compensatore di attrito deve essere inserito dopo aver effettuato l’analisi di stabilità del sistema retroazionato tramite il controllore PID.

Il compensatore in anello chiuso (Figura 5b) presenta il vantaggio che la sua uscita viene calcolata sulla base di un ingresso realmente misurato. Nonostante ciò, dato che la variabile di stato rappresentativa della deformazione della spazzola equivalente del modello non è una quantità misurabile, questo tipo di architetture richiedono l’utilizzo di osservatori dello stato.

In conclusione

In conclusione, i sistemi di posizionamento servo pneumatici con compensatori di attrito offrono significativi vantaggi in termini di precisione e stabilità. Sebbene la loro implementazione presenti alcune sfide, i benefici ottenuti in termini di prestazioni e affidabilità rendono questi sistemi una soluzione promettente per una vasta gamma di applicazioni industriali avanzate. La continua ricerca e sviluppo in questo campo porterà a ulteriori miglioramenti, contribuendo a rendere questi sistemi sempre più efficaci e accessibili.

Bibliografia

[1] Huang S, Liang W, Tan KK. Intelligent friction compensation: A review. IEEE/Asme Transactions On Mechatronics 2019;24:1763–74
[2] Al-Bender F, Lampaert V, Swevers J. Modeling of dry sliding friction dynamics: From heuristic models to physically motivated models and back. Chaos: An Interdisciplinary Journal of Nonlinear Science 2004;14:446–60
[3] Lentini L, Mazza L, Mossino G, Raparelli T. Modelling and Identification of a Pneumatic Positioning System: A Preliminary Study. The International Conference of IFToMM ITALY, Springer; 2022, p. 414–21
[4] Armstrong BS, Chen Q. The Z-properties chart. IEEE Control Systems Magazine 2008;28:79–89

Luigi Lentini, Luigi Mazza, Dipartimento di Ingegneria Meccanica ed Aerospaziale, Politecnico di Torino