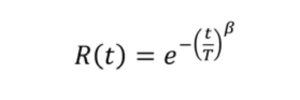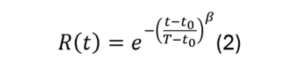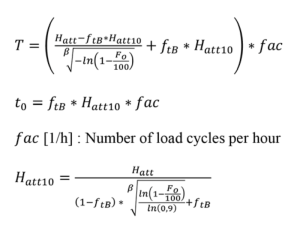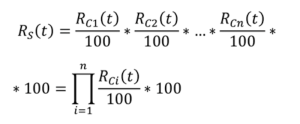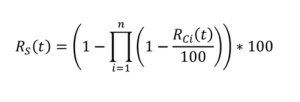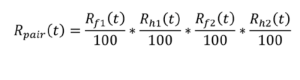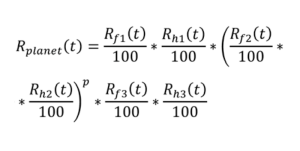Linee guida per il calcolo dell’affidabilità degli ingranaggi, con particolare focus su: calcolo della resistenza e della vita di servizio; definizione della probabilità di guasto; analisi dell’attendibilità di sistema.
L’affidabilità è un requisito sempre più cruciale nell’ingegneria meccanica, specialmente per i sistemi di trasmissione e i loro componenti chiave come gli ingranaggi. Questo articolo esplora i concetti fondamentali per il calcolo dell’affidabilità degli ingranaggi, partendo dal calcolo della resistenza e della vita di servizio, passando per la definizione della probabilità di guasto e dell’affidabilità, fino all’analisi dell’affidabilità di sistema. Viene posta particolare enfasi sull’utilizzo della distribuzione di Weibull per modellare il comportamento a fatica degli ingranaggi e sulla determinazione dell’affidabilità complessiva di accoppiamenti di ingranaggi e stadi epicicloidali. L’obiettivo è fornire un quadro metodologico per una progettazione più consapevole dei rischi e orientata alla durata.
Introduzione all’affidabilità nell’ingegneria meccanica
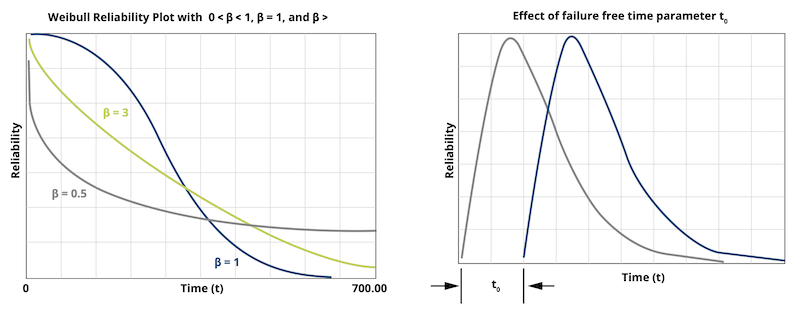
L’affidabilità di un sistema meccanico, e in particolare di un sistema di trasmissione, è una caratteristica sempre più richiesta in fase di progettazione. Nell’ingegneria meccanica, il termine “affidabilità” si riferisce alla probabilità che un componente o un sistema svolga la sua funzione prevista in condizioni operative definite per un periodo di tempo specificato. Tuttavia, storicamente, non è sempre esistito un linguaggio comune per interpretare i criteri di progettazione in termini di affidabilità. Ad esempio, gli ingegneri specializzati in ingranaggi tendono a preferire i “fattori di sicurezza“, mentre quelli che si occupano di cuscinetti si concentrano sulla “vita di servizio“. È fondamentale comprendere che la specificazione di un componente in termini di fattore di sicurezza, vita di servizio o affidabilità non è intrinsecamente differente. Questo documento si concentrerà sull’applicazione dei concetti di affidabilità al calcolo e alla progettazione degli ingranaggi. La Figura 1 illustra l’effetto del parametro di posizione (o tempo minimo prima del guasto) sulla funzione di densità di probabilità di Weibull, un concetto che verrà approfondito successivamente.
Calcolo della resistenza e vita di servizio degli ingranaggi
Metodi classici e fattori di sicurezza
Il metodo classico per il calcolo della resistenza degli elementi meccanici combina principi fondamentali della meccanica con valori empirici derivati dall’esperienza. Comunemente, le sollecitazioni risultanti determinate dal carico vengono confrontate con le sollecitazioni ammissibili. Tuttavia, le procedure di calcolo e la specificazione dei valori ammissibili possono variare significativamente a seconda dell’elemento meccanico, poiché sviluppate da specialisti di campi diversi.
Per gli ingranaggi, i criteri richiesti includono fattori di sicurezza minimi per il piede del dente (SFmin), il fianco del dente (SHmin) e il pitting (SBmin) (es. SFmin = 1.4, SHmin = 1.0, SBmin = 2.0). Per altri componenti come i cuscinetti, si richiede una vita minima Lnhmin, mentre per alberi e bulloni si specificano altri fattori di sicurezza minimi. Il risultato del calcolo per gli ingranaggi è tipicamente espresso in termini di fattori di sicurezza SF, SH, SB. La valutazione di un riduttore basata su questi diversi criteri può essere complessa, rendendo difficile determinare se le dimensioni siano adeguate per la vita target o quale sia il componente più debole.
Curve S-N e vita a fatica
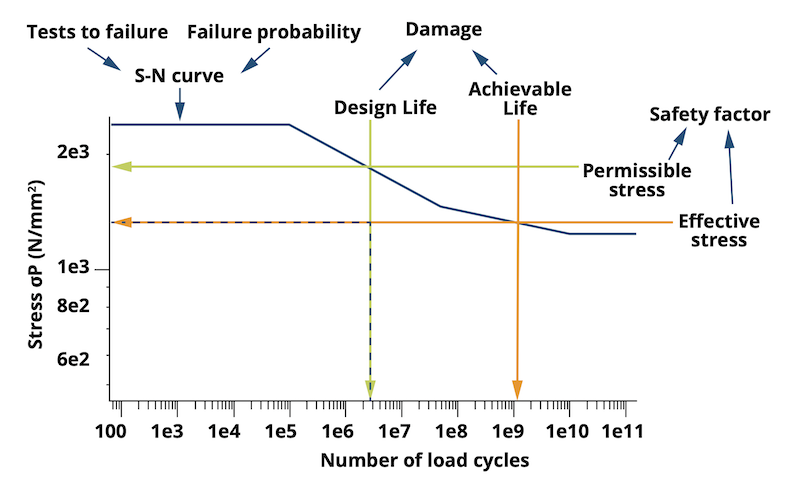
Tutti i calcoli che utilizzano una curva S-N del materiale (nota anche come linea di Wöhler) per definire la sollecitazione ammissibile possono essere usati per determinare la vita di servizio ottenibile, se sono specificati sia il fattore di sicurezza minimo (o richiesto) sia il carico applicato. Questo approccio è applicabile agli ingranaggi secondo normative come ISO 6336, DIN 3990 e AGMA 2101. La curva S-N rappresenta la sollecitazione ammissibile in funzione della vita (cicli di carico) ed è basata su test sperimentali, essendo correlata a una specifica probabilità di guasto. Questo permette un confronto diretto tra le vite di servizio calcolate per i diversi componenti, identificando l’elemento con la vita più breve come il più critico (Figura 2).
Terminologia Chiave
Alcuni termini fondamentali in questo contesto includono:
- Vita di progetto (Design life): numero di ore o cicli di carico per cui il componente o il riduttore è progettato per durare
- Vita ottenibile (Achievable life): numero calcolato di ore o cicli di carico che ci si aspetta il componente o il riduttore possa raggiungere
- Sollecitazione effettiva (Effective stress): il livello di sollecitazione che causa danno al componente, usato nel calcolo
- Sollecitazione ammissibile (Permissible stress): livello di sollecitazione per una data vita di progetto, usato per confronto con la sollecitazione effettiva
- Fattore di sicurezza (Safety factor): rapporto tra sollecitazione ammissibile e sollecitazione effettiva
Danno cumulativo e probabilità di guasto
Il concetto di danno
Il concetto di “danno” può essere un criterio utile per quantificare l’affidabilità dei componenti di una trasmissione e per localizzare rapidamente la parte più debole, specialmente in presenza di uno spettro di carico. Il danno può essere definito come il rapporto tra la vita di servizio richiesta e la vita di servizio ottenuta, moltiplicato per 100%:
Danno = Vita di servizio ottenutaVita di servizio richiesta × 100%
Per uno spettro di carico, il danno totale è la somma dei danni calcolati per ogni “bin” dello spettro. Un esempio di calcolo del danno per una coppia di ingranaggi considera il danno al piede del pignone (F1), al piede della ruota (F2), al fianco del pignone (H1) e al fianco della ruota (H2). Se il danno calcolato è pari a 0%, sorge la domanda su quanta riserva effettiva esista.
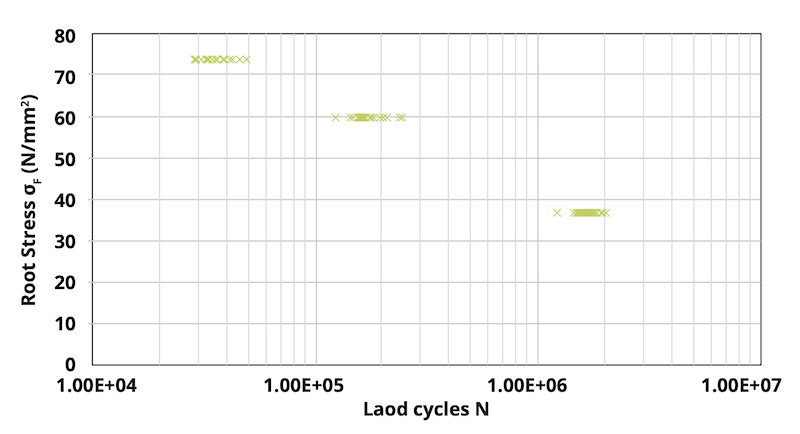
Natura Probabilistica delle curve S-N
Le proprietà dei materiali, e di conseguenza le curve S-N, sono determinate da test che presentano una natura intrinsecamente probabilistica. I test a un livello di carico specifico mostrano una dispersione dei cicli di carico fino al guasto. Questo richiede la definizione di un valore di probabilità associato alla curva S-N (Figura 3). Modificare la probabilità di guasto di riferimento sposta orizzontalmente la curva S-N, cambiando così la sollecitazione ammissibile. Di conseguenza, la probabilità di guasto del componente varia, e i danni calcolati non sono esatti con la stessa sicurezza matematica se le probabilità di guasto di riferimento per i diversi componenti o metodi di calcolo non sono omogenee.
Probabilità di guasto associata ai metodi di calcolo
A seconda del metodo di calcolo utilizzato, la probabilità di guasto per cui sono validi i valori di resistenza può variare significativamente. Ad esempio, per gli alberi, la DIN 743 e la direttiva FKM possono assumere una probabilità di guasto del 2,5% (anche se non sempre documentata), mentre la ISO 281 per i cuscinetti implica una probabilità del 10% se il fattore a1 è 1.0. Per il fianco e il piede del dente secondo ISO 6336 o AGMA 2001, la probabilità di guasto di riferimento è tipicamente dell’1% se il fattore di affidabilità YZ (o K_L per AGMA) è 1. Queste differenze rendono cruciale un approccio più unificato basato sull’affidabilità (Figura 4).
Definizione di affidabilità e la distribuzione di Weibull
Affidabilità come probabilità di sopravvivenza
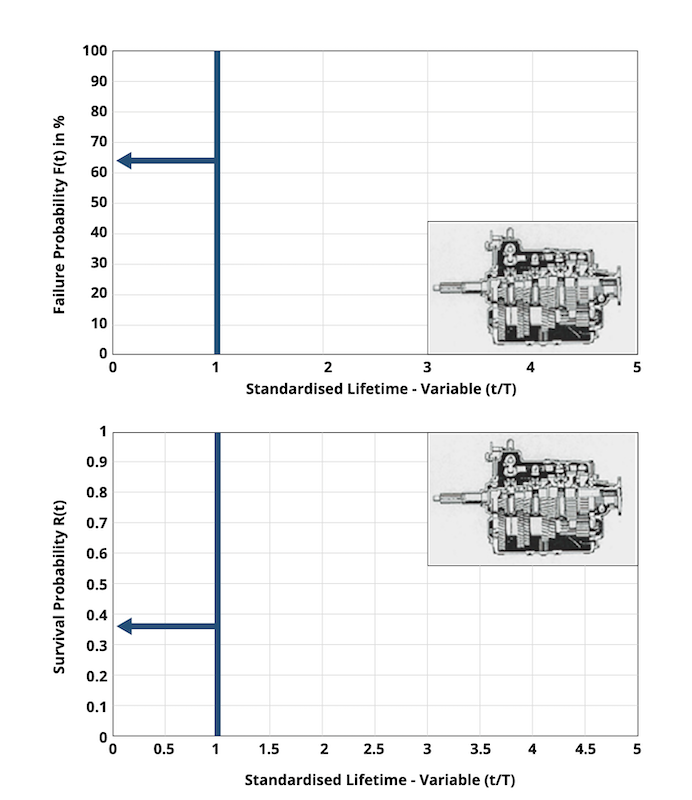
L’affidabilità (o Probabilità di Sopravvivenza) è definita come la probabilità che un prodotto non si guasti in condizioni funzionali e ambientali date durante un periodo di tempo definito (secondo la linea guida VDI 4001), Figura 5. Matematicamente, è il complemento della Probabilità di Guasto F(t): R(t) = 1 − F(t)
La distribuzione di Weibull a due e tre parametri
La distribuzione di Weibull è il tipo di distribuzione di probabilità più comune e ben adattato per descrivere l’affidabilità degli elementi meccanici. Esistono la distribuzione di Weibull a due parametri e quella a tre parametri; quest’ultima è raccomandata per l’ingegneria meccanica. La formula per l’affidabilità R(t) secondo la distribuzione di Weibull a due parametri è:
Mentre per la distribuzione di Weibull a tre parametri è:
Parametri della distribuzione di Weibull e loro significato
I parametri hanno il seguente significato:
- t: numero di cicli di carico o tempo di funzionamento
- t₀ (parametro di posizione o tempo minimo): numero di cicli di carico (o tempo) senza guasto. Nessun guasto si verifica durante i primi t₀ cicli. Questo parametro introduce un periodo iniziale durante il quale la probabilità di guasto è zero, il che è realistico per molti componenti meccanici che non falliscono immediatamente dopo l’entrata in servizio
- T (parametro di scala o vita caratteristica): vita caratteristica. Per t = T (e t₀ = 0), la probabilità di guasto è del 63.2%, corrispondente a un’affidabilità del 36.8%
- β (parametro di forma): definisce la forma della curva di distribuzione e può dare indicazioni sul meccanismo di guasto
Applicazione della distribuzione di Weibull agli ingranaggi
Determinazione dei parametri di Weibull dalla vita calcolata
I parametri T (vita caratteristica) e t₀ (tempo libero da guasti) possono essere determinati a partire dalla vita di servizio calcolata (Hatt) del componente e dalla probabilità di guasto (Fo) delle caratteristiche del materiale utilizzate nel calcolo iniziale.
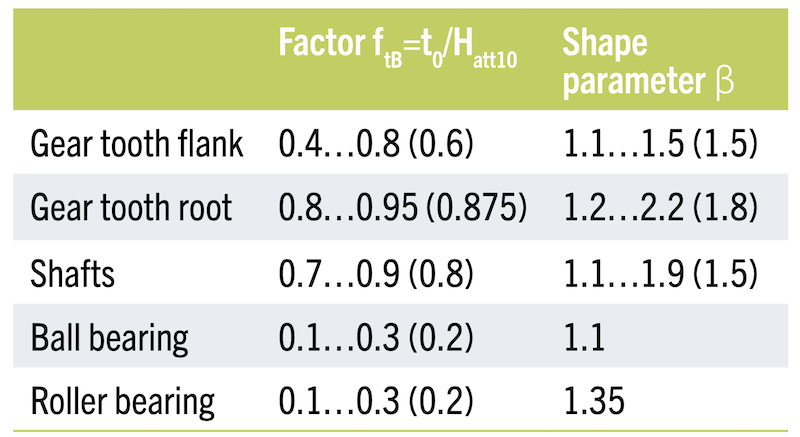
Le formule specifiche, come quelle proposte da Bertsche, legano Hatt, Fo, il fattore ftB = t₀ / Hatt10 (dove Hatt10 è la vita ottenibile per una probabilità di guasto del 10%) e il parametro di forma β (Tabella 1). Ad esempio:
dove “fac” è il numero di cicli di carico per ora.
Fattori Specifici per ingranaggi (piede e fianco del dente)
Bertsche fornisce valori raccomandati per il fattore ftB e il parametro di forma β per diversi componenti meccanici, inclusi gli ingranaggi. Per gli ingranaggi, si distinguono:
- Fianco del dente (Tooth flank):
• ftB: 0.4 … 0.8 (valore raccomandato: 0.6)
• β: 1.1 … 1.5 (valore raccomandato: 1.5) - Piede del dente (Tooth root):
• ftB: 0.8 … 0.95 (valore raccomandato: 0.875)
• β: 1.2 … 2.2 (valore raccomandato: 1.8)
Questi parametri possono essere definiti dall’utente nelle impostazioni specifiche del modulo di calcolo, sia per ingranaggi che per alberi e cuscinetti.
Esempio di calcolo dell’affidabilità per componenti di ingranaggi
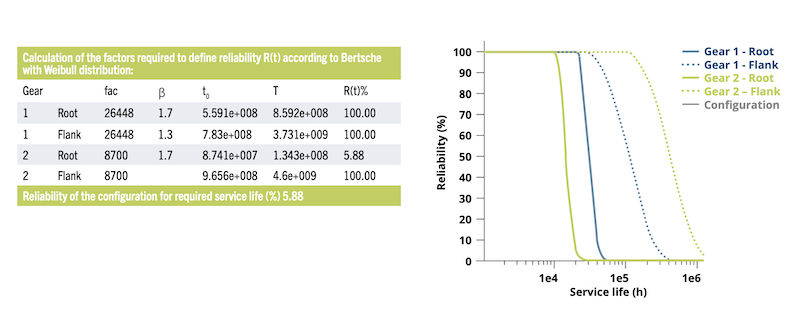
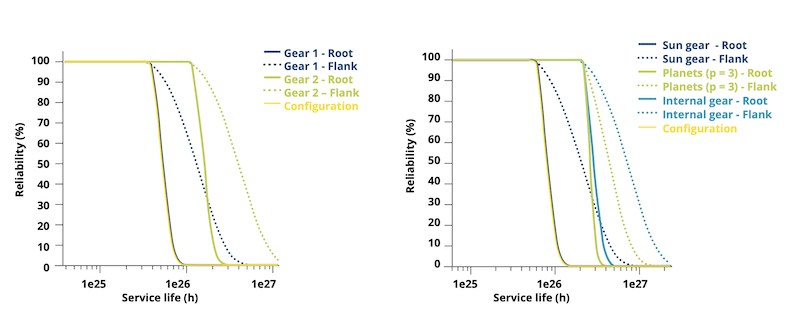
Una volta determinati i parametri β, t₀, e T, e noto il numero di cicli di carico per ora (fac), è possibile calcolare e tracciare l’andamento dell’affidabilità R(t) in funzione del tempo o del numero di cicli. La Figura 6 mostra un esempio di tali calcoli per il piede e il fianco di due ingranaggi, culminando nell’affidabilità della configurazione per la vita di servizio richiesta.
L’affidabilità espressa in percentuale (da 0 a 100) ha anche un importante effetto psicologico: mentre i fattori di sicurezza possono dare l’impressione di valori assoluti (un’alta sicurezza implica impossibilità di guasto), una rappresentazione dell’affidabilità, anche se del 99.99%, mostra sempre che un’incertezza residua permane.
Affidabilità del sistema di ingranaggi
Configurazione seriale e parallela
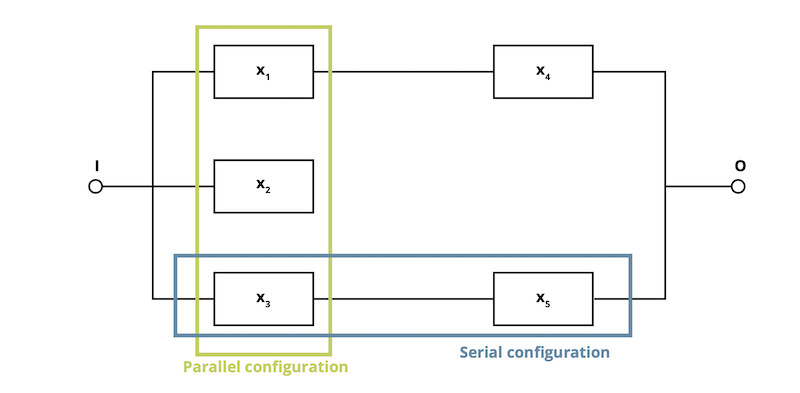
Il grande vantaggio dell’utilizzo dell’affidabilità come parametro per la qualificazione degli elementi meccanici è che l’affidabilità del sistema può essere determinata senza molto sforzo a partire dall’affidabilità dei singoli componenti. Per fare ciò, è necessario analizzare il diagramma a blocchi funzionale della trasmissione, classificando i componenti vitali in base alla loro disposizione (seriale o parallela) e verificando se esistono ridondanze. L’affidabilità del sistema viene quindi determinata da una combinazione matematica delle affidabilità dei componenti (Figura 7).
Per una configurazione seriale, l’affidabilità del sistema RS(t) è il prodotto delle affidabilità dei singoli componenti:
In un riduttore convenzionale, la rottura di un elemento importante (cuscinetto, albero, ruota dentata) causa di regola un guasto totale. Ciò significa che tutti questi elementi sono funzionalmente connessi in serie.
Per una configurazione parallela, l’affidabilità del sistema è data da:
Affidabilità di un accoppiamento di ingranaggi
Nel caso di un classico accoppiamento di ingranaggi, l’affidabilità totale Rpair(t) corrisponde al prodotto delle affidabilità dei quattro “elementi“: resistenza a piede (f) e a fianco (h), rispettivamente per il pignone (1) e la ruota (2):
Affidabilità di stadi epicicloidali
Negli stadi epicicloidali, il flusso di potenza è distribuito sui satelliti. Teoricamente, lo stadio potrebbe continuare a funzionare in caso di guasto di un satellite, poiché esiste una ridondanza. Tuttavia, in pratica, si considera spesso una connessione seriale degli elementi anche in questo caso, a causa delle conseguenze di un guasto parziale. L’affidabilità Rplanet(t) per uno stadio epicicloidale con “p” pianeti, considerando il sole (1), i pianeti (2), e la corona (3), e assumendo che il guasto di un qualsiasi componente porti al guasto dello stadio, può essere espressa come:
La formula specifica dipende dalla configurazione esatta e da quali elementi sono considerati critici per ogni componente (ad esempio, solare, satelliti, corona). La formula fornita in diapositiva 55 sembra riferirsi a Rf1, Rh1 per il solare, Rf2, Rh2 per ciascuno dei “p” satelliti, e Rf3, Rh3 per la corona interna.
Vantaggi della valutazione dell’affidabilità
L’uso dell’affidabilità come parametro per qualificare gli elementi meccanici offre un metodo robusto per determinare l’affidabilità del sistema complessivo. Fornisce una misura più chiara dell’incertezza residua rispetto ai tradizionali fattori di sicurezza, che possono dare una falsa sensazione di certezza assoluta.
Una nuova tendenza menzionata è l’esposizione del materiale (Material Exposure), come indicato nella direttiva FKM e ISO DTS 19042. L’esposizione è proporzionale al carico, mentre il danno è proporzionale alla vita di servizio. Per una considerazione più orientata al carico, l’esposizione del materiale può essere preferita al danno e alla vita di servizio.L’esposizione del materiale è definita come il rapporto tra la sicurezza richiesta e la sicurezza ottenuta.
Conclusioni e prospettive future
Il calcolo dell’affidabilità degli ingranaggi rappresenta un passo significativo verso una progettazione meccanica più robusta e consapevole. L’adozione di un approccio probabilistico, come quello basato sulla distribuzione di Weibull, permette di quantificare l’incertezza intrinseca nelle prestazioni a fatica dei materiali e di stimare la probabilità di sopravvivenza di un componente o di un intero sistema di trasmissione per una data vita di servizio.
La capacità di calcolare l’affidabilità dei singoli componenti (piede del dente, fianco del dente per pignone e ruota) e di combinarli per ottenere l’affidabilità di un accoppiamento di ingranaggi o di uno stadio epicicloidale, considerando configurazioni seriali o parallele, fornisce strumenti potenti per l’ottimizzazione del progetto e l’identificazione dei punti deboli. Questo approccio supera i limiti dei tradizionali fattori di sicurezza, offrendo una visione più realistica del comportamento del sistema nel tempo.
Le metodologie presentate, inclusa la definizione dei parametri di Weibull specifici per gli ingranaggi e la considerazione di spettri di carico attraverso il calcolo del danno, sono fondamentali per applicazioni critiche dove il guasto può avere conseguenze significative. Ulteriori sviluppi, come il concetto di esposizione del materiale, potrebbero affinare ulteriormente la valutazione della severità del carico sui componenti.
In conclusione, l’integrazione dei calcoli di affidabilità nella pratica ingegneristica standard per gli ingranaggi è essenziale per soddisfare le crescenti richieste di durata, sicurezza e prestazioni dei moderni sistemi meccanici.