Le Parole della Meccanica | Isostatico e Iperstatico

In meccanica i componenti delle macchine, e nella scienza delle costruzioni le membrature di una struttura, al fine di svolgere le proprie funzioni devono essere opportunamente vincolati, cosicché siano impediti i loro spostamenti, a meno di quelli necessari per il loro esercizio. Ciascun corpo, per ora considerato come rigido, possiede un certo numero di gradi di libertà, cioè di coordinate indipendenti che è necessario definire per individuarne univocamente la posizione. Si dice che un corpo è vincolato isostaticamente quando i vincoli applicati, o più correttamente i gradi di vincolo, sono quelli strettamente necessari a garantirne la stabilità, cioè sono in numero coincidente con i gradi di libertà. Se i vincoli sono invece in misura minore, il corpo può spostarsi ed è quindi ipostatico, cioè un cinematismo, come è necessario per alcuni componenti delle macchine la cui funzione è associata proprio al movimento.

Quando i vincoli applicati sono in eccedenza rispetto a quelli strettamente necessari a garantire la stabilità nell’ipotesi di corpo rigido, si ha invece una condizione di vincolo iperstatica. Il significato dei prefissi iso- e iper-, di origine greca, descrive proprio questa condizione di uguaglianza o di sovrabbondanza dei vincoli applicati rispetto a quelli indispensabili.

Isostatico e Iperstatico: approccio al calcolo

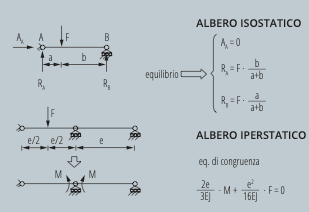
Una prima fondamentale differenza tra la condizione isostatica e iperstatica consiste nell’approccio al calcolo delle reazioni vincolari, cioè delle forze (e/o momenti) che i vincoli devono esercitare sul corpo in oggetto per garantirne l’equilibrio sotto l’azione dei carichi applicati: nel caso isostatico, le equazioni di equilibrio del corpo rigido sono sufficienti al calcolo di dette reazioni e il sistema che si sta considerando si dice anche, per questo motivo, staticamente determinato. Se invece il sistema è iperstatico, le sole equazioni di equilibrio non bastano e bisogna introdurre anche delle equazioni di congruenza, la scrittura delle quali implica la necessità di tener conto della deformabilità: si dice quindi che il sistema è staticamente indeterminato.

La minore semplicità dei calcoli necessari alla risoluzione del problema non è ovviamente un motivo ingegneristicamente valido per preferire una soluzione ad un’altra e la scelta si deve invece basare su altri aspetti rilevanti, riguardanti il comportamento in esercizio.

Prima di approfondire questo aspetto, mi soffermerò su alcuni esempi di vincolo iso- e iperstatico, prendendo come esempio un caso particolarmente significativo per la meccanica: l’albero di trasmissione.

Alcuni esempi di vincolo iso- e iperstatico

Dal punto di vista funzionale, l’albero è ovviamente un cinematismo, perché ruota attorno al proprio asse; se però prescindiamo da tale grado di libertà e ci concentriamo solamente sui vincoli necessari ad impedire spostamenti e rotazioni trasversali dell’asse, possiamo riconoscere che questo obbiettivo può essere ottenuto in modo isostatico, più frequentemente, ma anche iperstatico.

Nella maggioranza delle applicazioni, le proporzioni geometriche di un albero sono tali da poterne modellare il comportamento mediante lo schema della trave e pertanto ci riferimento a questo nel seguito. L’albero è un oggetto spaziale e necessità di un sistema di coordinate tridimensionale: lo studio può però essere ricondotto alla composizione dell’analisi su due piani perpendicolari e per questo motivo considereremo per semplicità una trave nel piano, la quale ci consente di discutere i principi fondamentali senza complicazioni inessenziali per questo fine. Una trave nel piano possiede 3 gradi di libertà, ad esempio le due coordinate ortogonali (x e y) necessarie a determinare la posizione di uno dei suoi estremi e un angolo che ne definisce l’orientamento. L’albero viene generalmente vincolato mediante cuscinetti, i quali, riguardo alla direzione assiale, possono essere bloccati o liberi (fixing, o locating, e floating in inglese). Nel primo caso impediscono sia gli spostamenti radiali che assiali, cioè sopprimono due gradi di libertà, e, nel linguaggio dei modelli a travi, sono identificati dal termine cerniera. Nel secondo invece, viene impedito il solo spostamento radiale e si utilizza il termine carrello.

Alla luce di quanto sopra, la combinazione di una cerniera e di un carrello è la condizione di vincolo minima e realizza la soluzione isostatica più frequentemente utilizzata per sostenere un albero.

Un albero su tre supporti, una cerniera e due carrelli, sarà invece iperstatico e potrà essere risolto abbinando alle tre equazioni di equilibrio un numero di equazioni di congruenza uguale a quello dei vincoli sovrabbondanti, pari a uno in questo caso (figura 2).

Un esempio interessante è quello di un albero montato su due cuscinetti di estremità obliqui, a sfere o a rulli conici, montati in opposizione (figura 3). Un cuscinetto obliquo si comporta da cerniera in uno dei due versi e da carrello in quello opposto: in altri termini, esercita in direzione assiale un vincolo monolatero. Nel caso di montaggio in opposizione senza precarico, ciò comporta che, a seconda del verso in cui agisca un carico assiale applicato, l’uno o l’altro in alternativa si comporti da cerniera, dando luogo in questo modo ad un sistema isostatico. Se invece, come spesso avviene per i cuscinetti di questo tipo, si introduce un precarico al montaggio, entrambi i cuscinetti lavorano contemporaneamente in direzione assiale e l’applicazione di una forza assiale determina, rispetto al precarico, un aumento di carico per uno e una corrispondente diminuzione per l’altro: di fatto si è realizzata una condizione iperstatica e l’effettiva distribuzione delle reazioni vincolari dipenderà dai rapporti di rigidezza tra i due elementi e sarà determinabile mediante un’equazione di congruenza. L’introduzione del precarico e la conseguente azione contemporanea dei due cuscinetti producono il vantaggio di un incremento di rigidezza del sistema, che potrà così sopportare forze assiali con spostamenti più piccoli.

In generale, riguardo al comportamento in esercizio, i montaggi isostatici presentano il vantaggio di non subire l’influenza di effetti termici sulle reazioni vincolari e sugli sforzi interni: ad esempio, un albero vincolato con cerniera e carrello, sottoposto ad una temperatura più elevata di quella della struttura che lo supporta, sarà libero di dilatarsi in direzione assiale in misura maggiore di quest’ultima, evitando così la nascita di sforzi assiali derivanti dalla coazione termica, diversamente da quanto accadrebbe se vi fossero due cerniere. Inoltre, le reazioni vincolari dei sistemi isostatici non sono influenzate dai cedimenti di vincolo (strutture civili) o dalle tolleranze di costruzione delle costruzioni meccaniche: ad esempio, un albero su tre supporti sarà soggetto ad azioni flessionali derivanti da un non perfetto allineamento degli stessi.

Pur a fronte di tali svantaggi, talvolta i montaggi iperstatici non possono essere evitati,  quando vi sia la necessità di incrementare la rigidezza: è ad esempio il caso di alberi lunghi, per limitare le deflessioni trasversali, o di applicazioni per le quali la rigidezza sia fondamentale, come nel settore delle macchine utensili.