Le molle sono elementi di macchine aventi la capacità di deformarsi molto rimanendo nel campo elastico del materiale del quale sono costituite, cioè senza subire deformazioni plastiche. Questa proprietà dipende non solamente dalle caratteristiche meccaniche del materiale, al quale è richiesto di avere un ampio campo elastico nel diagramma sforzi deformazioni, ma anche dall’utilizzo una geometria opportuna, in grado di dar luogo alla deformabilità desiderata.
Le molle sono utilizzate per realizzare sistemi di sospensione, per accumulare energia potenziale elastica, per introdurre elementi elastici di caratteristica opportuna nella trasmissione delle forze e del movimento.
Generalmente le molle sono classificate mediante due differenti criteri, come visibile in figura 1. Secondo il primo, che si basa sull’azione interna prevalente, si possono avere molle di:
- trazione-compressione
- torsione
- flessione.
Il secondo classifica invece le molle in accordo alla lore geometria:
- molle elicoidali
- molle a balestra
- molle ad anelli
- barre di torsione
- molle a spirale
- ….
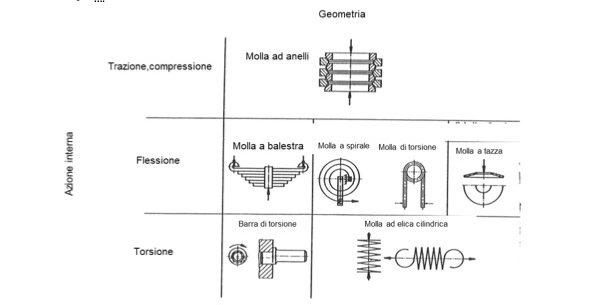
Nella realizzazione costruttiva, le molle devono anche prevedere gli elementi necessari al collegamento e all’applicazione del carico: ad esempio, le barre di torsione devono avere estremità idonee al loro afferraggio, le molle ad elica cilindrica devono avere le spire di estremità spianate se destinate ad essere compresse o dei ganci se per la trazione, e così via.
Il comportamento di una molla è descritto dalla curva caratteristica, cioè dalla curva che descrive l’andamento della forza applicata in funzione dello spostamento F=F(f) (o momento in funzione dell’angolo M=M(f)). La tangente alla curva caratteristica identifica la rigidezza della molla:
K = dF/df
In relazione all’andamento della curva si hanno tre possibilità: se è una retta, la rigidezza è costante e la molla è lineare e si ha quindi:
K = F/f
La molla si dice invece dolce, quando la rigidezza decresce all’aumentare del carico e dura quando aumenta.
In prevalenza, le molle sono realizzate in acciaio utilizzando acciai specificamente concepiti per questa applicazione: gli acciai per molle sono acciai legati, ad alta resistenza e, come anticipato, sono caratterizzati da un valore del carico di scostamento dalla proporzionalità poco distante da quello di rottura (oltre 85%).
Metodo di calcolo delle molle
Nel seguito è presentata una sintesi del metodo di calcolo delle molle ad elica cilindrica sottoposte a carico assiale. Esse sono costituite da un filo, che nel caso più frequente ha sezione circolare, avvolto ad elica con passo costante su di un cilindro retto: si tratta di una geometria particolarmente favorevole che si presta ad ottenere il valore di rigidezza desiderato con ingombri ridotti.
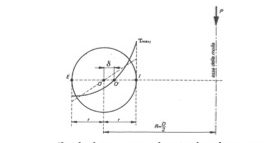
La figura 2 mostra i principali parametri geometrici della molla.
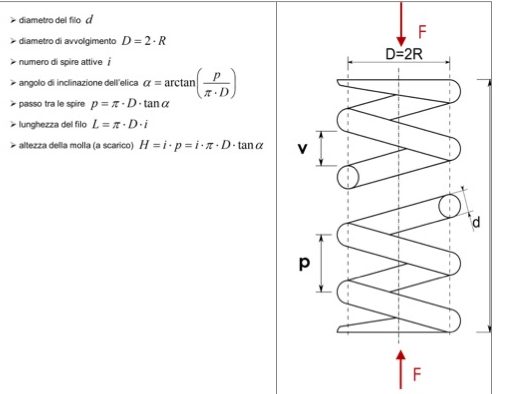
Le azioni interne prodotte nel filo dall’applicazione di una forza diretta come l’asse della molla sono costituita da torsione, taglio, flessione e azione assiale come indicato in figura 3.
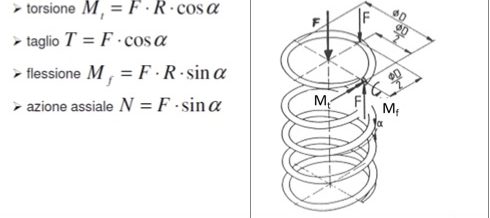
Se il valore dell’angolo d’elica è piccolo, tale per cui il suo coseno può essere approssimato con l’unità e il seno ritenuto prossimo a zero (indicativamente minore di 8°), le azioni assiale e flessionale divengono trascurabili e le sollecitazioni prevalenti rimangono la torsione e il taglio. Nel calcolo elementare, si considera la sola sollecitazione di scorrimento t prodotta dal momento torcente, e ciò equivale a considerare il filo della molla come una barra di torsione, disposta ad elica invece che ad asse rettilineo. La sollecitazione di torsione vale pertanto:
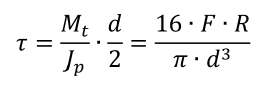
Il calcolo della rigidezza può essere eseguito uguagliando il lavoro esterno della forza applicata che produce lo schiacciamento della molla (1/2 Ff) al lavoro dell’azione interna di torsione che produce una rotazione relativa tra le estremità del filo (1/2 Mtj): svolgendo i passaggi che vengono qui omessi, si ottiene la seguente espressione per la rigidezza:
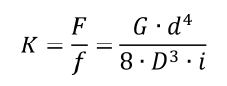
L’equazione mostra che la rigidezza della molla dipende linearmente dal modulo elastico del materiale (che vi compare attraverso il modulo di elasticità tangenziale G), ma molto più sensibile è l’influenza del diametro di avvolgimento (che insieme al numero di spire dà luogo all’ingombro) e di quello del filo.
L’approssimazione nei valori di sforzo ottenuti con il calcolo elementare è accettabile quando il rapporto tra il diametro di avvolgimento D e quello del filo d (identificato dal parametro C = D/d) non è troppo piccolo. Al diminuire di C aumentano infatti gli effetti dovuti alla presenza di uno sforzo dovuto all’azione di taglio T e all’influenza della curvatura del filo sugli sforzi di torsione, che non sono distribuiti in modo lineare nella sezione come nel caso di una barra rettilinea, ma che hanno invece l’andamento mostrato in figura 4.
Il calcolo esatto evidenzia che sforzo massimo, che si ha all’intradosso del filo, può essere ottenuto moltiplicando quello del calcolo elementare per il coefficiente di Wahl, dato dalla seguente espressione:
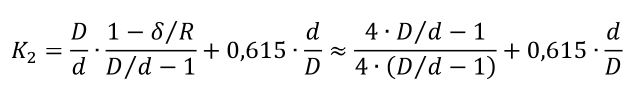
Svolgendo i calcoli si vede che, ad esempio, con un valore di C=6 lo sforzo massimo è del 25% più elevato di quello del calcolo elementare. Con C=10 l’errore è poco meno del 15%. Non vi è invece necessità di correggere il valore di rigidezza restituito dal calcolo elementare.
La verifica della molla si effettua confrontando lo sforzo calcolato con i limiti del materiale, statici o a fatica in relazione alle condizioni di esercizio. Per le molle si è soliti eseguire la verifica “a pacco”, cioè in corrispondenza del carico che produce il completo schiacciamento con le spire in aderenza: oltre tale condizione, un aumento di carico non produce più un aumento dello sforzo di torsione e pertanto esso costituisce la condizione statica più sfavorevole alla quale la molla può potenzialmente essere sottoposta.


