Le prove pulsatore sono la metodologia più efficace per investigare le proprietà resistenziali del piede dente. Questo articolo discute l’uso di prove sperimentali effettuate tramite pulsatore all’interno di una verifica agli spettri di carico
La progettazione di un treno di ingranaggi richiede numerosi passaggi. La prima fase consiste nel pre-dimensionamento, in cui vengono scelti parametri chiave come modulo e larghezza di fascia. Successivamente inizia la progettazione vera e propria dove, tramite numerose iterazioni, viene definita la geometria ottimale e viene definita la macro e micro geometria dei denti. In questa fase di affinamento occorre tenere in considerazione numerosi aspetti come la deformabilità dei componenti, la lubrificazione ed il rumore. Inoltre, bisogna anche considerare che il riduttore difficilmente lavora costantemente sotto lo stesso carico ma che esso è soggetto ad un certo spettro di carico.
Questo aspetto è trattato ampiamente dallo standard ISO 6336-6:2019 [1], che è anche consigliato da ANSI AGMA 2001-D04 [2]. Da un lato, la norma propone un metodo di calcolo utile atto alla definizione di un carico equivalente da usare nelle fasi di pre-dimensionamento. Dall’altro, permette di calcolare un coefficiente di sicurezza rispetto allo spettro di carico stimato. Questo standard si applica sia alla fatica da contatto che per la fatica flessionale al piede dente. Tre sono le basi di questo standard: lo spettro di carico, una legge di accumulo del danno (la regola di Palmgren-Miner [3,4]) e una curva SN nota. Tale curva può essere ricavata all’interno del contesto normativo [2,5–7]. In ogni caso, al fine di allontanarsi dalla natura generica degli standard, usando quindi dati relativi allo specifico campo industriale, il progettista può sempre affidarsi a prove sperimentali atte alla definizione di tale curva; tale aspetto è anche consigliato dagli standard stessi.
Nel caso della fatica piede dente, ovvero il nostro caso di interesse, la curva SN può essere ricavata tramite numerosi metodi come le prove su provini intagliati, le prove pulsatore e le prove con ruote ingrananti. Al momento, tra queste, il metodo più adottato sono le prove pulsatore. Tali prove, infatti, utilizzano un provino rappresentativo (ovvero i denti di una ruota dentata a denti dritti) senza usare però una macchina di prova specializzata, perciò una qualunque macchina di prova universale è in grado di effettuare tali test. Occorre però rimarcare che le prove pulsatore sono effettuate senza ingranamento: i denti sono caricati da dei punzoni e non dall’ingranamento con un’altra ruota. Pertanto, i risultati di tale metodologia devono essere rielaborati prima di usare l’evidenza sperimentale per la verifica di una coppia di ingranaggi.
Il risultato finale di tale rielaborazione è una curva SN definita ad un certo livello affidabilistico (tipicamente 99% di affidabilità, ovvero 1% di probabilità di cedimento). Queste curve possono essere usate per la verifica a spettro di una coppia di ingranaggi. In prima analisi, tali curve possono differire dalle curve suggerite dagli standard (vedi [2,7]) per via delle intrinseche differenze di materiali. Inoltre, in base al modello di elaborazione adottato, si possono ottenere curve differenti. È quindi logico pensare che anche il risultato della verifica a spettro possa essere diverso rispetto a quello ottenuto seguendo gli standard.
Questo articolo tratta appunto tale argomento: l’uso dell’evidenza sperimentale ottenuta tramite prove pulsatore così come la successiva elaborazione all’interno del contesto più ampio della verifica a spettro. Inoltre, viene qui investigato come il risultato di tale verifica possa differire dal risultato ottenuto seguendo un approccio puramente normativo.
A tal fine, occorre introdurre la metodologia di prova e le procedure di elaborazione, spiegando poi come la normativa suggerisce di effettuare la verifica a spettro. Successivamente vengono presentati due casi di studio basati su spettri di carico misurati specificamente su applicazioni ad ingranaggi per poi discuterne i risultati.
L’analisi qui riportata si basa su cinque serie di prove effettuate su ingranaggi cementati usando un pulsatore “simmetrico”. Tali prove sono qui chiamate “A”, “B”, “C”, “D” ed “E” e sono state realizzate dagli autori di questo articolo.
Prove pulsatore come metodologia di prova per la fatica flessionale piede dente
Tutte le prove atte ad investigare la resistenza degli ingranaggi presentano una non banale difficoltà: il meccanismo di cedimento di interesse (ad esempio: la fatica flessionale piede dente) deve risaltare rispetto agli altri fenomeni (ad esempio: fatica da contatto, grippaggio). Questo problema viene risolto in due modi: o si disegna un provino che risulta essere particolarmente debole rispetto al cedimento di interesse o, come nel caso della fatica flessionale piede dente, si adotta una metodologia di prova in cui è presente un solo cedimento.
Le prove pulsatore sfruttano appunto quest’ultima idea. La fatica piede dente viene replicata applicando tramite opportuni punzoni un carico alternato in una posizione fissa del fianco. Non essendo presente l’ingranamento, è chiaro che tutti i fenomeni legati all’ingranamento (es. fatica da contatto) non sono presenti e non alterano la prova. Le prove pulsatore possono essere realizzate in numerosi modi: caricando un albero dentato su un punzone (es. [8]), eseguendo prove di flessione su tre punti (es. [9]), ad un dente (prova asimmetrica, es. [10,11]) o a due denti (prova simmetrica, es. [12,13]). Si rimanda il lettore interessato a [10,14] per un’analisi dettagliata della metodologia di prova.
Elaborazione delle prove pulsatore
La mancanza dell’ingranamento implica alcune differenze tra il caso del pulsatore ed il caso reale, dove le ruote dentate ingranano sotto carico. Da un lato, queste differenze sono legate al dissimilare affaticamento del piede dente per via della diversa storia di carico [15]. Dall’altro, sono presenti discrepanze di natura statistica. Infatti, nelle prove pulsatore il dente che cede è predeterminato mentre nel caso dell’ingranamento la rottura della ruota è identificata nel cedimento del suo dente più debole (es. [16]). Pertanto, a causa di tali differenze, occorre elaborare i dati sperimentali prima di usarli nelle fasi progettuali.
Non sorprende quindi che tale problema nasca con la definizione della metodologia di prova stessa. Infatti, già nel 1964, quando Seabrook e Dudley presentarono i loro primi risultati ottenuti sui denti, osservarono come i dati sperimentali necessitassero di essere elaborati per renderli rappresentativi del caso reale [8]. Alla fine degli anni ’90 sono state presentate altre metodologie come quella proposta da Rao e McPherson [17,18] e il report FVA 304 [12]. Recentemente sono stati pubblicati nuovi lavori sull’argomento da parte degli autori di questo articolo (es. [14,15,19]), così come da parte di Hong [10].
Tutti questi approcci condividono tre differenti aspetti. Per prima cosa, come in tutte le prove di fatica, occorre elaborare i dati di fatica. Rao e McPherson [17,18] adottano uno staircase modificato per la stima sia della fatica a termine che per vita illimitata. Il report FVA 304 [12] adotta una procedura staircase per trovare il limite di fatica ed un semplice fitting per la vita limitata, unendo poi i due tratti per definire l’intera curva. [14,19] invece propone l’uso del metodo della Massima Verosimiglianza (MV) per stimare i parametri di una curva SN univoca: nello specifico, viene utilizzato il modello di Spindel–Haibach [20]. Anche Hong [10] utilizza il metodo MV ma per stimare i parametri di una curva differente.
Successivamente l’evidenza sperimentale rilevata sui denti viene riferita alla ruota. Tipicamente questo viene effettuato usando coefficienti correttivi (come in [12]) o usando correlazioni statistiche (come in [10,14,17,18]).
L’ultimo passaggio richiede di tenere in considerazione la differente condizione di carico. Questo aspetto viene trattato tramite coefficienti correttivi come quello del Rettig [16] (come in [12], dove questo coefficiente viene applicato alla fatica a vita illimitata) o altri approcci simili al diagramma dello Haig.
Interessante notare come tutte le metodologie proposte suggeriscano una scalatura simile dei dati pulsatore; o meglio, come esse producano un risultato simile, specialmente nella zona della fatica a vita illimitata della curva SN.
Modelli statistici adottati
Tra le diverse metodologie adottate, questo articolo si concentra su quella descritta dal report FVA 304 [12] e sull’uso della MV unita alla statistica degli estremi [14]; entrambe sono state sviluppate guardando ad una configurazione simmetrica. È possibile trovare una loro descrizione completa nel numero di luglio 2023 di Organi di Trasmissione così come nelle loro fonti originarie (ovvero [12,14]). Le curve stimate seguendo il report FVA 304 sono qui chiamate “FVA, D.P” e “FVA, L.F.” in base alla presenza di una doppia pendenza o di un limite di fatica nella regione a vita illimitata. Similmente, le curve ottenute usando MV per stimare i parametri del modello Spindel-Haibach e la statistica degli estremi sono qui chiamate “S.H.-2T” e “S.H.-STBF” seguendo la nomenclatura presentata precedentemente.
Entrambi i metodi di cui sopra usano una formulazione bi-lineare (o tri-lineare) per descrivere la curva SN; conseguentemente, il campo SN è descritto da una serie di linee inclinate e/o orizzontali. Tale assunzione rappresenta una semplificazione del problema della fatica che risulta in una chiara distinzione tra le diverse regioni della curva SN senza mostrare una transizione tra le due regioni. Conseguentemente, per ovviare a questo limite statistico, i modelli statistici proposti da Pascual e Meeker (ovvero il “random fatigue limit” [21]), e quello proposto da Castillo e Fernández-Canteli, (ovvero il modello “Weibull a tre parametri” [22]) sono stati introdotti nel contesto del metodo MV e statistica degli estremi. Ovvero, la MV viene usata per stimare la curva sperimentale e la statistica degli estremi è stata usata per trasferire l’evidenza sperimentale all’ingranaggio. Le curve ottenute da questi modelli sono qui chiamate “R.F.L.” e “3 P.WBL”. Tali modelli sono stati inclusi per via del loro forte fondamento teorico e l’uso di solo 5 parametri, numero relativamente basso.
Come suggerito nel report FVA 304 [12], l’effetto delle diverse condizioni di carico è stato preso in considerazione applicando il coefficiente correttivo definito dal Rettig [16].
Tale coefficiente, chiamato fP → MG, è pari a 0.9 ed è stato applicato sul parametro dei modelli che più si avvicina al concetto di limite di fatica.
Al fine di considerare le differenze tra le prove pulsatore (elaborate) ed il contesto normativo occorre considerare due ulteriori curve. Queste sono ricavate adottando il limite di fatica della ruota dentata in condizioni di ingranamento come base per ricavare il σflim da norma e, sempre sfruttando la ISO 6336-3 [7], ricavare le curve secondo normativa ISO. Queste due ultime curve sono qui chiamate “ISO, D.P.” e “ISO, F.L.” in base alla presenza di una doppia pendenza o di un limite di fatica.
La tabella 1 riassume i vari modelli adottati mentre la figura 1 mostra le diverse curve stimate per la campagna sperimentale “E”.
| Tabella 1 | ||||
| Nome | Forma della curva SN | Stima dei parametri | Differenza statistica | Differenza del ciclo di carico |
| FVA, L.F. | Bilineare, con limite di fatica | FVA 304 | FVA 304 | fP → MG su σ(F0∞, 50&,P) |
| FVA, D.P. | Trilineare, con pendenza secondaria | FVA 304 | FVA 304 | fP → MG su σ(F0∞, 50&,P) |
| S.H., STBF | Bilineare | MV | Statistica degli Estremi | fP → MG su σe |
| S.H., 2T | Bilineare | MV | Statistica degli Estremi | fP → MG su σe |
| RFL | Continua, con limite di fatica | MV | Statistica degli Estremi | fP → MG su Y |
| 3 P.WBL | Continua, con limite orizzontale | MV, usando ProFatigue [23] | Statistica degli Estremi | su C |
| ISO, L.F. | Bilineare, con limite di fatica | ISO 6336 e FVA 304 | FVA 304 | fP → MG su σ(F0∞, 50&,P) |
| ISO, D.P. | Bilineare | ISO 6336 e FVA 304 | FVA 304 | fP → MG su σ(F0∞, 50&,P) |
La verifica a spettro secondo normativa ISO
Il progettista che vuole considerare la presenza di spettri di carico può fare affidamento sullo standard ISO 6336-6 [1]. Per fare questo, vengono richiesti tre diversi ingredienti.
Primo, occorre determinare lo spettro, e lo standard permette sia l’uso di spettri misurati che di spettri stimati. Tale spettro deve essere poi suddiviso in circa una sessantina di livelli di carico.
Successivamente, occorre conoscere la curva SN del componente. Nel contesto ISO, tale curva può essere ricavata sperimentalmente o, in alternativa, usando i valori di limite di fatica previsti dalla ISO 6336-5 [5] ed i coefficienti correttivi contenuti nei vari standard di riferimento (ISO 6336-2 [6] per la fatica da contatto e ISO 6336-3 [7] per la fatica flessionale).
Occorre poi adottare una legge di danneggiamento e, tra le varie leggi presenti nella letteratura scientifica, lo standard propone l’uso del modello di danneggiamento lineare proposto da Palmgren [3] e Miner [4]. Secondo tale legge, il danno può essere calcolato come:
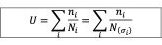
(1)
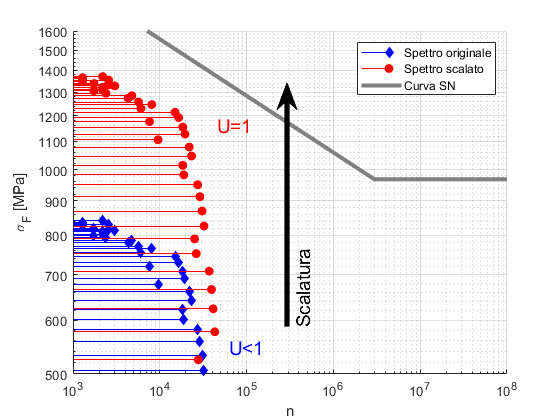
Dove ni è il numero di cicli associato all’i-esimo livello di carico e N(σi) è il massimo numero di cicli che determina il cedimento (ad un certo livello affidabilistico) al livello di carico σi. Se il danno cumulato U supera l’unità, la verifica non è soddisfatta. La ISO 6336-6 [1] propone un metodo per il calcolo di un coefficiente di sicurezza S andando, sul diagramma SN, a scalare lo spettro nella direzione degli sforzi. Più nel dettaglio, S è quel coefficiente di scalatura che porta al danneggiamento unitario. La figura 2 mostra un esempio di tale metodo di calcolo: lo spettro originale (in blu) è scalato di , andando così a definire quello spettro (in rosso) che porta a U = 1.
Caso 1: riduttore per sollevatore industriale
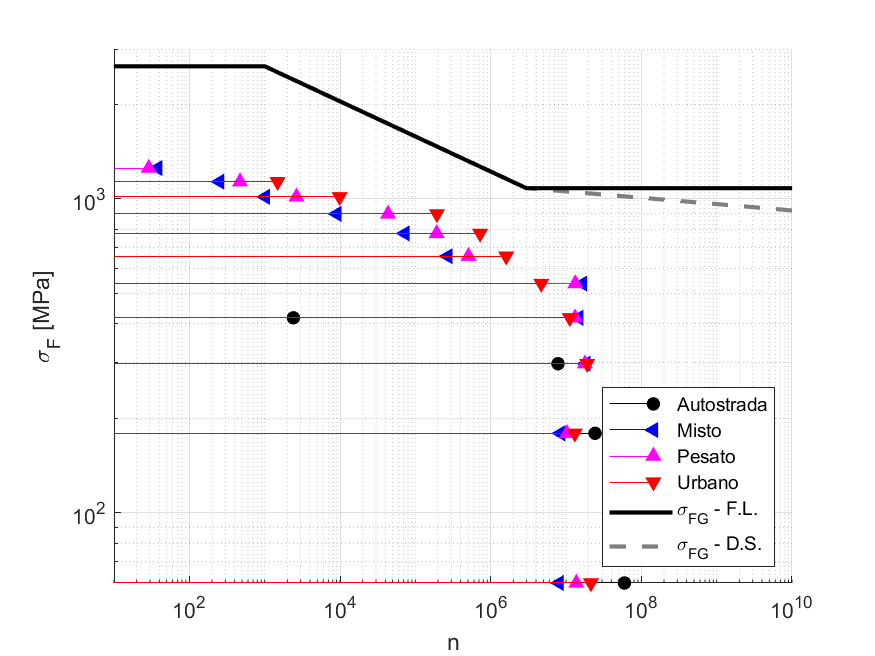
Il primo esempio di spettro di carico qui considerato è uno spettro misurato su un riduttore di un sollevatore industriale (“industrial hoist” nella versione originale) ed è riportato nella normativa ISO 6336-6 [1]. Questo spettro, misurato su 70 giorni di esercizio, è stato poi estrapolato per essere rappresentativo di 30 anni. La norma riporta anche il materiale della ruota e la sua geometria, permettendo così di ricavare le due curve SN secondo normativa (con o senza il limite di fatica). I risultati ottenuti usando queste curve sono indicati nei grafici come “σFG,L.F. e σFG,D.P.”. Lo spettro e la curva secondo normativa sono riportate in figura 3.
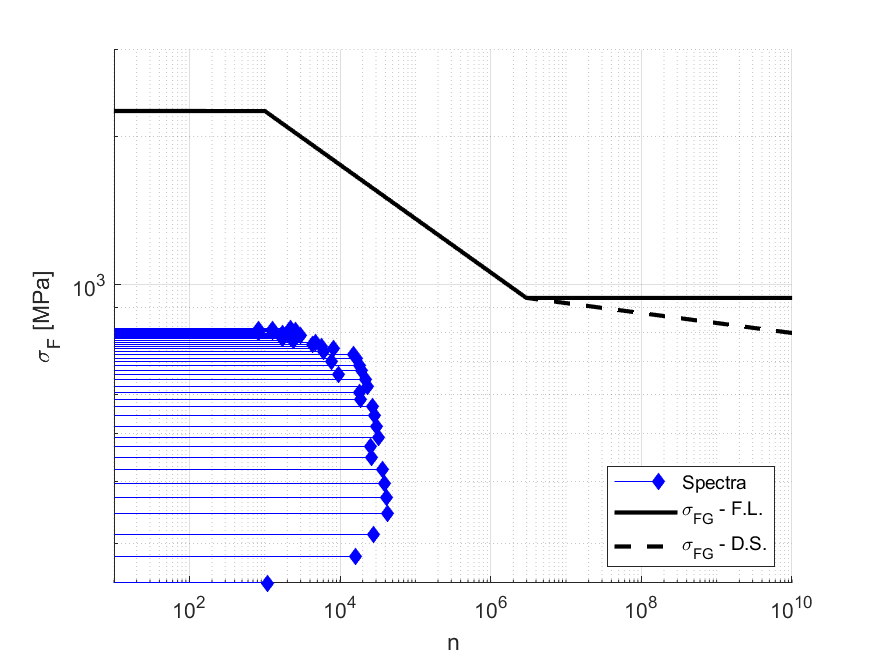
Le 5 campagne sperimentali prese qui come esempio sono state effettuate su ruote cementate ma, per via delle diverse variazioni di processo e di materiale, risultano avere tutte delle differenti proprietà di resistenza in quanto, di fatto, realizzate di materiale diverso (inteso come combinazione della tipologia di acciaio e di trattamento). Inoltre, hanno anche proprietà resistenziali che differiscono da quelle previste dallo standard. Per ovviare a questo problema, lo spettro è stato scalato sulla base del rapporto tra il limite di fatica calcolato secondo FVA 304 e quello definito seguendo le indicazioni delle norme. In questo modo è possibile rimuovere le discrepanze tra i vari test, evidenziando così solo le differenze tra i vari modelli statistici adottati così come quella tra essi e le curve da normativa.
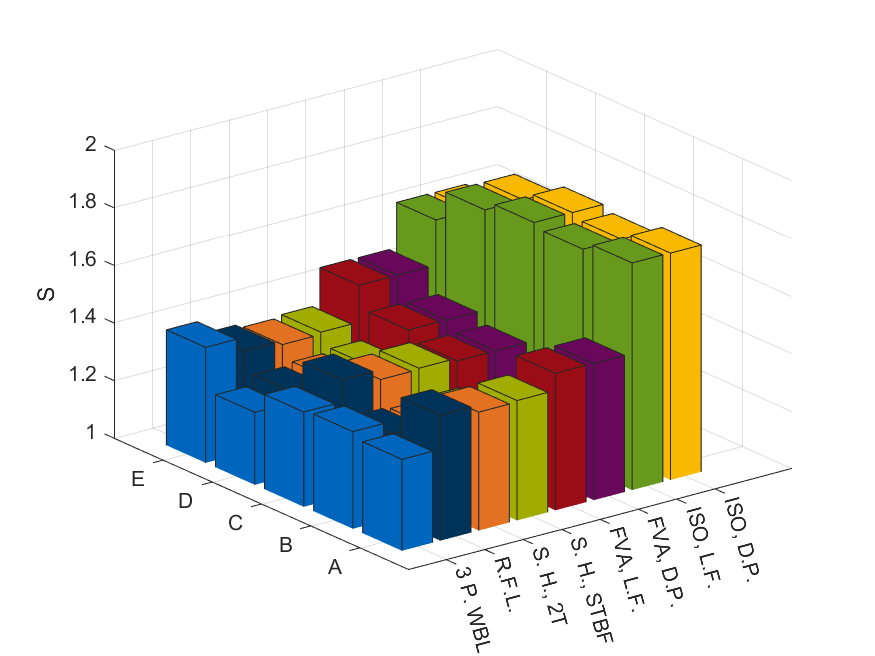
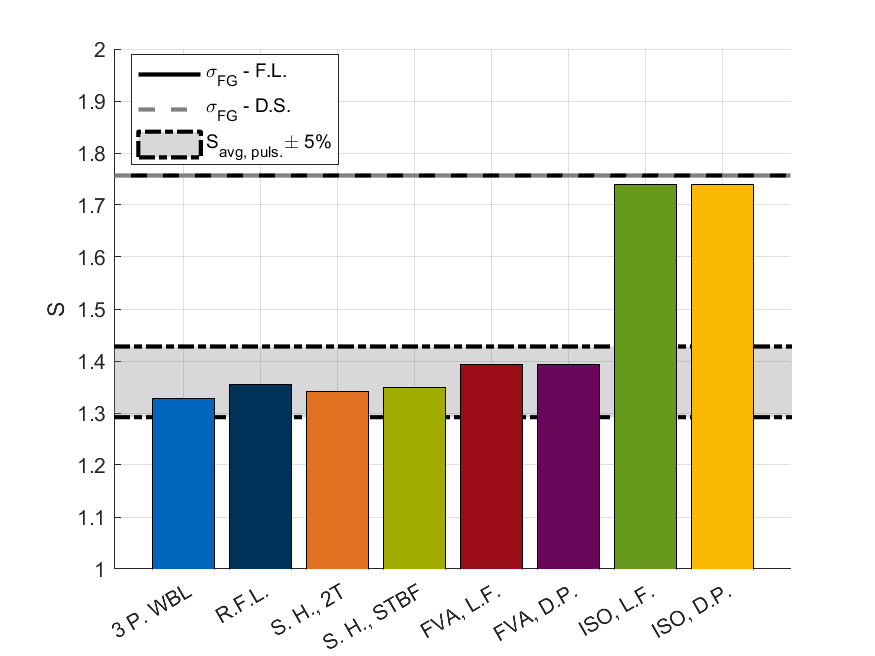
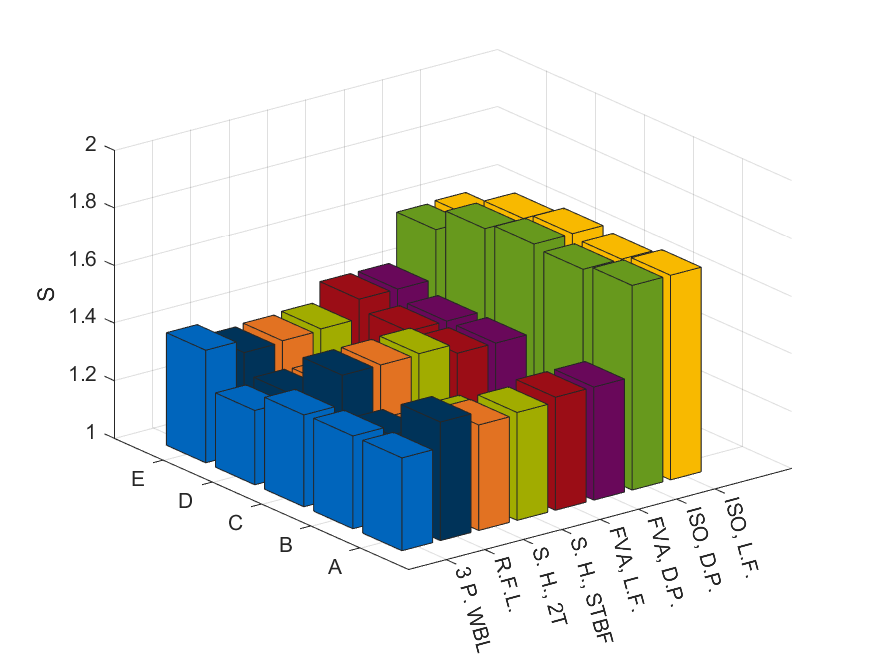
La figura 4 mostra i vari coefficienti di sicurezza, mentre la figura 5 li riporta mediati rispetto alla campagna sperimentale.
Caso 2: trasmissione intermedia di camion
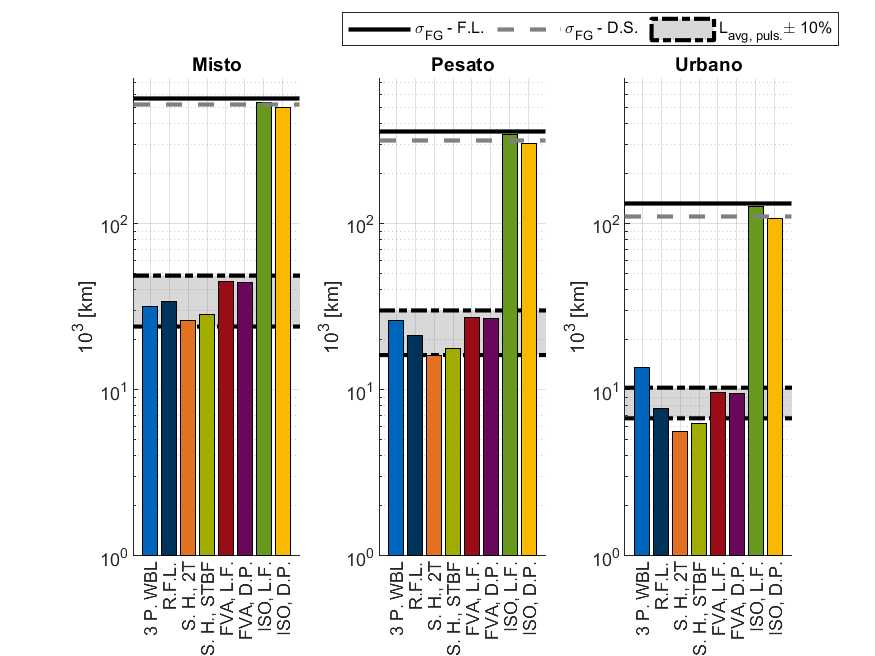
Il secondo caso di studio qui esaminato è uno spettro di carico misurato sulla ruota di ingresso di una trasmissione intermedia di un camion misurato da Curà [24], membro del comitato scientifico di questa rivista (n.d.r.). Nel suo lavoro, sono presenti 4 diversi spettri, chiamati “Autostrada”, “misto strada e montagna” (di seguito “Misto”), “strade urbane” (di seguito “Urbano”) “missione totale pesata” (di seguito “Pesato”). Tali spettri sono stati misurati lungo missioni (ovvero viaggi) di circa 100 km principalmente nella zona del Piemonte e dell’appenino tosco-emiliano (ad esempio, guidando da Torino ad Aosta, da Susa al Colle del Moncenisio e da Borgo Taro a Pontremoli). Anche Curà riporta sia la geometria che il materiale della coppia di ruote, permettendo così di ricostruire anche in questo caso la curva secondo normativa, oltre allo lo spettro. Le componenti negative dello spettro non sono state considerate. I diversi spettri di carico, così come le curve secondo normativa sono riportate in figura 6.
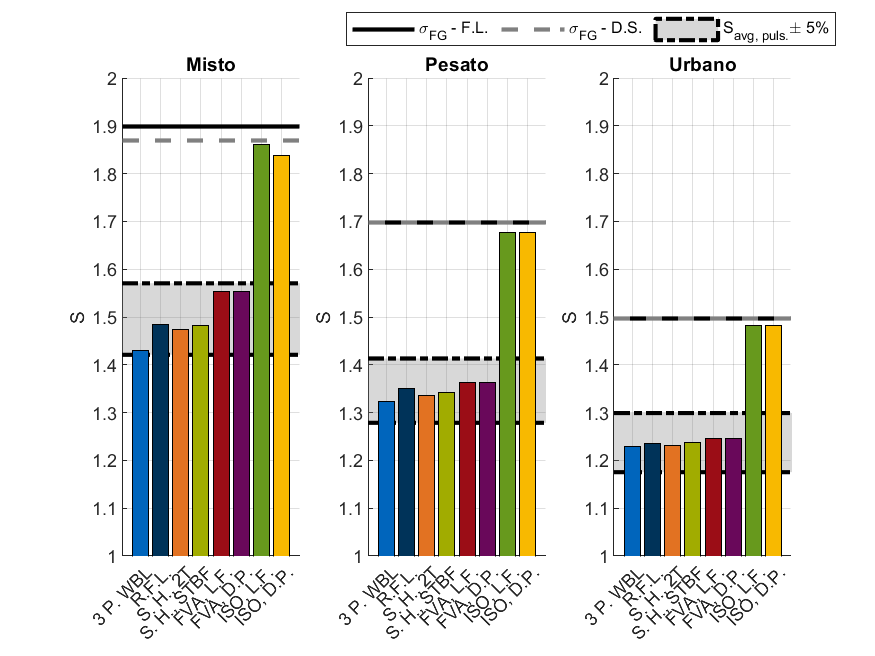
Similmente a quanto fatto per il caso 1, anche in questo caso è possibile calcolare il coefficiente di sicurezza per ogni spettro. Anche in questo caso, le curve ricavate dalle evidenze sperimentali sono state scalate per mantenere inalterato il posizionamento relativo tra di loro e lo spettro. La figura 7 riporta i risultati di tale calcolo per lo spettro “Pesato” mentre la figura 8 riporta il valore mediato per i tre spettri di interesse. Lo spettro “Autostrada” non è stato incluso perché posizionato molto in basso rispetto alla curva SN (vedi figura 6), fornendo un coefficiente di sicurezza minimo maggiore di 3.
In ogni caso, il concetto di coefficiente di sicurezza ha solo un mero significato ingegneristico. In questo specifico caso, è possibile fornire un senso fisico ai calcoli non lavorando su S ma, sempre restando all’interno del modello di danneggiamento lineare, andando a calcolare la vita utile del camion o, meglio, andando a calcolare la vita utile del componente preso in esame in termini di km percorribili prima del supposto cedimento al livello affidabilistico considerato, che è pari ad 1% di probabilità di cedimento. Questo può essere fatto calcolando il danno U generato da ogni singola ripetizione dello spettro, da cui è possibile ricavare il numero di ripetizioni Nr come:
Nr * U = 1 (2)
Più specificatamente, Nr rappresenta quante volte una particolare missione può essere ripetuta. Sapendo che ogni spettro è stato misurato su missioni effettive di 100 km, è possibile ricavare quindi il numero di chilometri massimi percorribili.
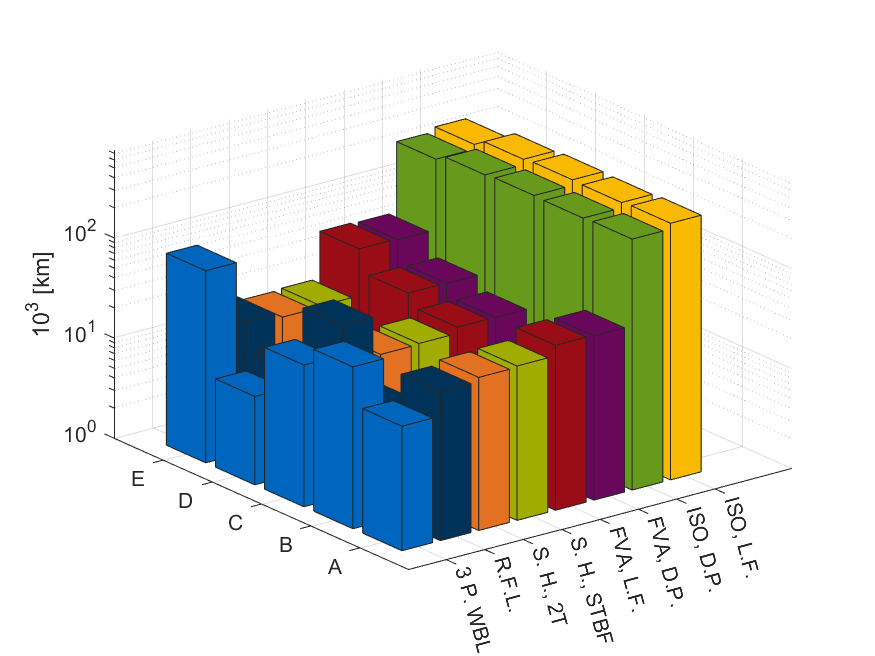
La figura 9 riporta la vita utile calcolata per lo spettro “Pesato” mentre la figura 10 ne riporta il valore meditato per i tre spettri di interesse. Il risultato è espresso in migliaia di chilometri per semplicità di lettura dei risultati. Anche in questo caso lo spettro “Autostrada” non è stato riportato.
Risultati
Le cinque campagne sperimentali di prove al pulsatore effettuate su ruote dentate cementate riportate in [19] (chiamate “A”, “B”, “C”, “D” ed “E”) sono state sfruttate per ricavare numerose curve SN riferite alla ruota dentata, in condizioni di ingranamento ed a una probabilità di cedimento dell’1%. Tutte queste curve, derivate usando diversi metodi statistici, sono state usate per effettuare una verifica a spettro seguendo la normativa ISO 6336-6 [1]. La tabella 1 riassume tali curve. Anche le curve ricavate secondo normativa ISO per gli ingranaggi presentati nei documenti riportanti gli spettri sono state incluse. Gli spettri presi in considerazione appartengono al settore industriale ed al settore automobilistico. Più precisamente, il primo spettro si riferisce ad un sollevatore industriale [1] mentre gli altri ad una trasmissione intermedia di un camion industriale [24].
Al fine di ridurre l’effetto delle differenze dei vari valori resistenziali ottenuti sperimentalmente, così come dello scarto tra tali valori e quello delle ruote riportate in [1,24], è stato scelto di scalare gli spettri. È possibile notare la validità di tale operazione guardando a figura 5, figura 8 e figura 10. Infatti non vi è una differenza sostanziale tra i risultati delle curve “ISO, L.F.” e “ISO, D.P.” e il risultato ottenuto secondo la ISO 6336-3 [7]. La piccola discrepanza è legata a differenze nella pendenza del tratto a termine tra quello riferito alle ruote testate e quello proposto delle ruote riportate in [1,24].
Inoltre, è possibile osservare come, giustamente, il risultato della verifica a spettro risulta essere influenzato dal modello statistico preso in considerazione. In ogni caso, non è possibile identificare un metodo che risulti essere maggiormente conservativo: di fatto non vi è un posizionamento relativo dei risultati che risulti essere constante.
Guardando lo stesso spettro ma con materiali differenti è possibile identificare un esempio di quanto detto poco sopra nei risultati delle curve “3 P.WBL” e “R.F.L.” per i materiali “A” ed “E” del caso 1 (vedi figura 4): per il materiale “A” il coefficiente di sicurezza ottenuto con “3 P.WBL” è inferiore rispetto a quello ricavato da “R.F.L.” mentre per il materiale “E” il posizionamento risulta essere invertito. Un ulteriore esempio sono le curve “S.H., STBF/2T” e “FVA, L.F./D.P.” per i materiali “A” e “C” per lo spettro “Pesato” (vedi figura 7). Anche il caso della vita utile stimata presenta esempi simili (vedi “R.F.L.” e “S.H., STBF/2T” per i materiali “A” e “C”, figura 9).
I risultati si mantengono comunque relativamente simili tra loro: per il caso dei coefficienti di sicurezza ricadono tutti in un intervallo ±5% il valor medio e per la vita utile in un intervallo ±10% (su scala logaritmica). Con gli spettri e i materiali presi in considerazione, questa analisi sembrerebbe indicare che la scelta di una particolare curva, con un maggiore (o minore) fondamento statistico, così come la scelta di includere o meno una pendenza nel tratto della vita illimitato non abbiamo un particolare effetto in una verifica a spettro secondo normativa ISO, ovvero basata su una legge di accumulo lineare del danno.
La differenza non è però tra i modelli che interpretano l’evidenza sperimentale ma tra loro e i risultati ottenuti con le curve da normativa; più nel dettaglio, le prove pulsatore, elaborate, forniscono sempre un risultato più conservativo (ovvero minor coefficiente di sicurezza o una minor vita utile stimata) rispetto alla ISO 6336. Questa differenza è imputabile alla diversa posizione del ginocchio della curva SN che, per tutte le prove pulsatore qui considerate, è posizionato al di sotto dei cinquecentomila cicli. Diversa invece è la posizione proposta dalle normative ISO 6336-3 [7] e ANSI AGMA 2001 D04 [2], le quali pongono il ginocchio a tre milioni di cicli.
È possibile dare una interpretazione “ingegneristica” dell’effetto di tale discrepanza guardando la vita utile stimata riportata in figura 9. Assumendo che lo spettro “Pesato” sia rappresentativo delle reali condizioni di lavoro di un camion, la vita utile stimate sulla base delle prove sperimentali è, in media, circa ventiduemila chilometri; valore ben al di sotto di ciò che può essere considerato un valore tipico per un camion. D’altro lato, le curve basate sull’uso della normativa ISO 6336-3 [7] forniscono una vita utile di circa trecentomila chilometri, valore relativamente basso ma, sicuramente, più vicino a quello reale.
Perché tale differenza e come gestirla?
Resta da capire se la differenza della posizione del ginocchio è presente solo nei punti sperimentali o se tale differenza sia legata a dei comportamenti più generali. Per approfondire questo aspetto è stata effettuata una ricerca bibliografica su campagne sperimentali per la fatica flessionale piede dente effettuate sia tramite pulsatore, sia con ruote ingrananti. La ricerca bibliografica sulle prove pulsatore, più disponibili in letteratura, è riportata in tabella 2, dove sono riportate campagne effettuate da metà anni ’60 fino ai giorni nostri (sempre su ruote cementate). Tra queste 269 campagne, 18 mostrano un ginocchio posizionato ad un numero di cicli maggiore o uguale ad un milione di cicli mentre 248 a un numero minore o uguale a cinquecentomila cicli. L’esperienza degli autori suggerisce che la posizione del ginocchio non cambi significativamente anche dopo l’obbligatoria elaborazione dell’evidenza sperimentale delle prove pulsatore. Pertanto, tali valori possono essere considerati rappresentativi delle curve finali.
Al contrario, le poche campagne effettuate tramite ruote ingrananti presenti nella letteratura scientifica (ovvero, [12,25,26]) riportano il ginocchio posizionato al di sopra del milione di cicli. Nel dettaglio, [12] riporta un grafico collettivo di 6 campagne in cui il ginocchio è posizionato ad un milione di cicli, [25] presenta 5 campagne il cui ginocchio è posizionato tra i due ed i quattro milioni di cicli mentre [26] 3 campagne il cui ginocchio è al di sopra di dieci milioni di cicli. Tali valori sono simili al tre milioni di cicli previsto dalla normativa tecnica [2,7].
| Tabella 2 | ||||
| Autore e riferimento | Anno | Numero totale di punti sperimentali | Numero di campagne riportate | Numero di cicli del ginocchio |
| McIntire [27] | 1966 | 177 | 16 | 14 tra 105 e 5*105 2 tra 5.1*105 e 106 |
| Kato [28] | 1986 | 171 | 2 | 1 ≈. 5*105 1 ≈ 106 |
| Inoue [29] | 1989 | 265 | 18 | ≈ 1 105 (tutte) |
| Kato [30] | 1993 | 392 | 9 | 7 > 106 2 < 5*105 |
| Inoue [31] | 1994 | 215 | 4 | 1 ≈ 106 1 ≈ 5*105 2 ≈ 2*105 |
| Yang [32] | 1996 | 104 | 1 | ≈ 3*106 |
| Stahl [12] | 1999 | 2219 | 93 | ≈ 5*105 (valor medio) |
| Stenico [25] | 2004 | ≈ 350 | 16 | 4 oltre 1*106, 10 tra 1*105 e 5*105 2 sotto 1*105 |
| Masuyama [33] | 2004 | 28 | 2 | ≈ 7*105 (tutte) |
| Yamanaka [34] | 2007 | 56 | 4 | < 2*105 (tutte) |
| Yamanaka [35] | 2010 | 56 | 4 | 1 a 9*104 3 a 2*105 |
| Zhang [36] | 2013 | 45 | 1 | 6*105 |
| Dobler [37] | 2015 | No dichiarato | 4 | 4 <= 5*105 |
| Olsson [38] | 2016 | No dichiarato | 2 | 1 a 9*104 1 a 3*105 |
| Conrado [39] | 2017 | 40 | 2 | 2 a 2 105 |
| Meneghetti [40] | 2017 | 32 | 1 | ≈ 8*104 |
| Lambert [41] | 2018 | 5 | 5 | 1 a 3*106 1 ≈ 1*106 3 < 3*105 |
| Argoud [42] | 2019 | 28 | 1 | < 105 |
| Bonaiti [19] | 2022 | 1643 | 76 | ≈ 5*105 (tutte) |
| Lisle [43] (temperatura ambiente) | 2022 | ≈ 200 | 6 | 1 > 3*106 1 ≈ 6*105 4 < 5*105 |
| Kratzer [44] | 2022 | 21 | 1 | 3*105 |
| Sun [45] | 2023 | 40 | 1 | ≈ 106 |
Tutto ciò suggerisce che vi sono delle differenze intrinseche tra le prove pulsatore e lo scenario reale delle ruote ingrananti e che tali differenze non sono state ancora considerate. Ne consegue che, quando si vuole considerare la vita limitata e la sua transizione verso la vita illimitata, l’applicazione del coefficiente del Rettig [16] o di altre metodologie non sia sufficiente visto che altri effetti potrebbero essere presenti ma non ancora considerati.
Una teoria che potrebbe fare luce su questo aspetto è lo studio dell’effetto che la presenza di cricche nel piede dente potrebbe avere sulla rigidezza del dente che, conseguentemente, altererebbe la ripartizione del carico tra i denti (ad esempio [46]). Nello specifico, la rigidezza di un dente “criccato” risulterebbe essere minore, riducendo il carico nelle fasi dell’ingranamento in cui è in presa più di una coppia di denti. Questo riduce la sollecitazione del piede dente, rallentando la propagazione della cricca [47]. Chiaramente, questo aspetto non è presente nelle prove pulsatore: il carico è sempre applicato sugli stessi denti, senza fenomeni di ripartizione di carico.
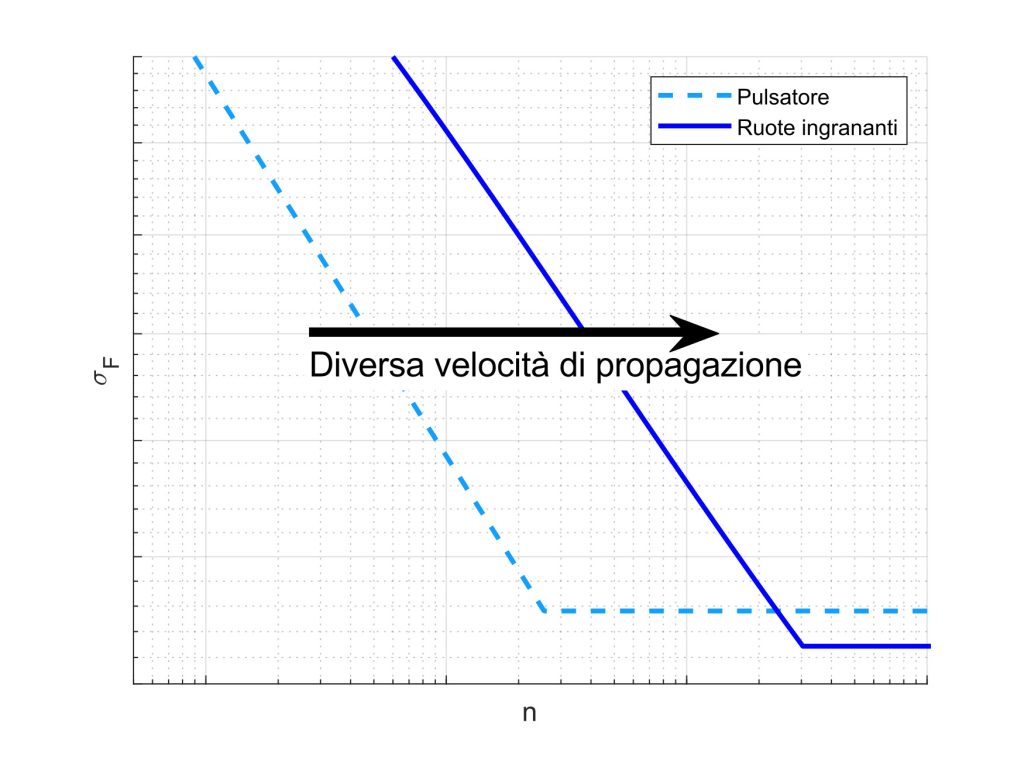
A questo punto, occorre introdurre teoria del Murakami [48], la quale suggerisce che la vita a fatica limitata e quella a fatica illimitata siano in realtà legate ad aspetti differenti. Nello specifico, nella zona prima del ginocchio (ovvero la zona a vita limitata) le cricche nucleano e propagano fino al cedimento del componente mentre, dopo il ginocchio (la vita illimitata) le cricche possono nucleare ma la loro propagazione si arresta. L’applicazione di tale teoria nel nostro caso di interesse suggerisce che l’effetto della diversa velocità di propagazione legato alla differente ripartizione del carico infici solo la zona a vita limitata, non quella a vita illimitata. Ovvero, come spiegato da figura 11, l’effetto di tale differente ripartizione del carico tra i denti causa uno spostamento lungo l’asse orizzontale della curva SN, il quale va a modificare sicuramente la zona a vita limitata, lasciando inalterata la zona a fatica illimitata (essendo questa orizzontale). Di conseguenza, le prove pulsatore possono essere ancora usate per stimare il limite di fatica dei denti, da poi riportare al caso reale.
Ne consegue che un uso meno conservativo delle prove pulsatore nelle fasi di verifica a spettro sarebbe impiegarle per ricavare il limite di fatica della ruota (ovvero ISO σflim o ANSI AGMA Sat). Successivamente, derivare la curva SN usando la curva tipo ed i fattori correttivi di cui sopra. La motivazione di tale scelta si basa, da un lato, sui risultati ottenuti per il caso 2 e, dall’altro, su quanto discusso poco sopra.
In ogni caso, occorre rimarcare come siano necessarie nuove campagne sperimentali di prove di fatica flessionale piede dente, effettuate sia tramite pulsatore che tramite ruote ingrananti e sullo stesso ingranaggio campione volte ad investigare la stessa regione della curva SN. Al momento non sono presenti indagini simili nella letteratura tecnico/scientifica. Tali prove permetterebbero di aumentare la conoscenza della metodologia di prova, premettendo quindi di ridurre le differenze tra questo metodo sperimentale ed il caso reale, dove le ruote ingranano sotto carico.
Le prove pulsatore restano comunque una metodologia di prova ben consolidata e adatta per stimare i valori resistenziali (il limite di fatica) in maniera efficace ed efficiente e i valori da esso ottenuti, ovviamente rielaborati, possono essere usati all’interno dei codici di calcolo della normativa ISO e della normativa AGMA. Il tutto anche se, come visto sopra, i risultati ottenuti investigando la regione di vita illimitata non possano essere trasferiti direttamente alla condizione di ruote ingrananti senza la opportuna esperienza. In ogni caso, è comunque possibile usare il pulsatore nella zona di vita limitata per studi comparativi; ovvero prove atte ad investigare l’effetto di varianti progettuali (geometrie, materiali, trattamenti) sulla sensibilità ai sovraccarichi.
Conclusioni
All’interno del più ampio contesto della verifica di una coppia di ingranaggi rispetto alla fatica flessionale piede dente, questo articolo discute l’uso di prove sperimentali effettuate tramite pulsatore all’interno di una verifica agli spettri di carico. Il punto di partenza di questo articolo sono una serie di prove sperimentali, degli spettri di carico e delle ruote di cui materiale (nominale) e geometria sono noti.
Le prove sono state analizzate utilizzando numerosi metodi statistici e poi applicando dei coefficienti correttivi, ottenendo dalle prove effettuate sui denti delle diverse curve sperimentali riferite all’ingranaggio in condizioni di ruote ingrananti ed a una probabilità di cedimento dell’1%. Le metodologie applicate sono da considerarsi, al momento, lo stato dell’arte. La verifica agli spettri di carico è stata effettuata nel contesto della norma ISO 6336-6 [1], ovvero usando una legge di accumulo lineare del danno per poi calcolare un coefficiente di sicurezza così come la vita utile stimata. Per ridurre le differenze tra il materiale investigato nelle prove ed il materiale nominale è stato necessario scalare gli spettri al fine di lasciare inalterato loro posizionamento rispetto alle curve. Sono stati presi in considerazione numerosi spettri, uno riferito ad un sollevatore industriale e tre riferiti alla trasmissione intermedia di un camion.
Parlando delle curve ottenute dalla elaborazione delle prove sperimentali, si è visto come non sia presente un sostanziale impatto delle metodologie con cui si effettua tale elaborazione. Non è infatti presente un risultato particolare in termini di posizionamento relativo dei vari risultati e, a conti fatti, tutte le curve producono dei valori tra loro completamente comparabili e non significativamente differenti.
La vera differenza non è però tra le prove pulsatore ed i risultati che da esse derivano ma tra tali risultati e quelli ottenuti seguendo un approccio secondo normativa ISO. Ciò è legato alla differente posizione del ginocchio della curva SN, il quale risulta essere posizionato al di sotto dei cinquecentomila cicli per le prove pulsatore, mentre le normative [2,7] lo propongono a 3 milioni di cicli. Come mostrato dalla ricerca bibliografica, tale discrepanza non è legata alle prove qui usate: si tratta di un comportamento generale delle prove pulsatore, la cui evidenza sperimentale suggerisce una posizione ben diversa da quella che le prove effettuate su ingranaggi rotanti indicano come rappresentativa della fatica flessionale piede dente.
Ne consegue che il progettista che volesse usare le prove pulsatore come base per una verifica a spettro deve essere conscio di tali differenze e che, se è vero che le tali prove forniscono dati specifici, essi sono anche conservativi rispetto allo scenario reale, dove le ruote dentate ingranano sotto carico.
Luca Bonaiti, Marco Monti, Carlo Gorla, Dipartimento di ingegneria meccanica, Politecnico di Milano
Michael Geitner, Thomas Tobie, Karsten Stahl, Institute of Machine Elements, Gear Research Centre FZG), Technical University of Munich






