Guide lineari e viti a ricircolo di sfere: caratteristiche e metodi di calcolo
La movimentazione lineare di precisione è una necessità fondamentale nell’ambito dell’ingegneria e dell’automazione.
Per eseguire un movimento lineare occorrono principalmente due componenti: un organo di generazione del moto lineare e un elemento di guida.
Il moto lineare può essere generato direttamente, tramite attuatori lineari come motori elettrici lineari, cilindri pneumatici o idraulici oppure trasformando il moto rotatorio generato da un motore elettrico tramite un sistema a vite. Questo secondo caso è attualmente il più diffuso, soprattutto per quanto riguarda il posizionamento di precisione.
Esistono sostanzialmente due tipologie di guide e viti: quelle basate su attrito radente (come le guide a coda di rondine che venivano utilizzate nelle macchine utensili, piuttosto che le più recenti guide in tecnopolimero e per quanto riguarda le viti di manovra, troviamo i tipici profili trapezoidali) e quelle che invece sfruttano l’attrito volvente, cioè il rotolamento relativo di corpi, che possono essere sfere o rulli.
Questa seconda tipologia rappresenta la più utilizzata soprattutto nelle applicazioni dove sono richieste elevate prestazioni sia in termini di precisione che di carichi e velocità di movimentazione. Attualmente, le guide lineari e le viti a ricircolo di sfere sono componenti che svolgono un ruolo essenziale nel supporto del movimento preciso in una vasta gamma di applicazioni industriali e tecnologiche. Queste guide sono progettate per fornire un supporto di precisione a carichi lineari, consentendo movimenti fluidi e regolari.
In questo articolo ci focalizzeremo quindi sulla tecnologia di movimentazione volvente, esploreremo cosa sono le guide lineari e le viti a ricircolo di sfere, come funzionano, le loro applicazioni comuni e i vantaggi che offrono.
Cos’è una guida lineare a ricircolo di sfere?
Le guide lineari a ricircolo di sfere possono essere divise in due grandi categorie: le guide lineari con manicotti e le guide lineari a pattini (figura 1).
Entrambe sono costituite da un elemento di guida, un elemento mobile (manicotto per il primo tipo e pattino per il secondo) e degli elemini volventi interposti fra elemento di guida e elemento mobile che per i manicotti sono sfere, mentre per le guide a pattini possono essere sfere o rulli.
Per le guide a manicotti l’elemento di guida consiste in una barra a sezione circolare, mentre per le guide a sfere è un elemento dalla geometria più complessa che definiremo come rotaia.

(cortesia: Bosch Rexroth)

Come funzionano le guide lineari a ricircolo di sfere?
Il funzionamento delle guide lineari a ricircolo di sfere è relativamente semplice, ma altamente efficace. Le sfere all’interno dei pattini o dei manicotti permettono al carrello di scorrere lungo le guide mediante il ricircolo dei corpi volventi, questi ultimi ricircolano all’interno dei pattini e vengono trasportati dai pattini stessi durante il loro movimento sulle rotaie (figura 2). La corsa massima del sistema viene limitata soltanto dalla lunghezza delle guide. Questo riduce l’attrito e garantisce che il movimento sia costante e preciso.
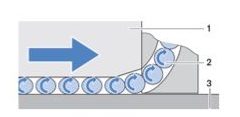
I copri volventi, sfere o rulli, sono quindi sollecitati dai carichi esterni e il loro comportamento strutturale può essere descritto dalla teoria di Hertz che considera il comportamento di due corpi aventi superfici curve compressi l’uno contro l’altro da una forza e consenti il calcolo delle tensioni e deformazioni nella zona di contatto. L’impronta di contatto sarà teoricamente puntiforme nel caso di sfere e lineare nel caso di rulli. I secondi presentando una superficie di contatto maggiore, consentono di sopportare carichi maggiori, pagando però in termini di prestazioni dinamiche che risulteranno limitate rispetto ai corpi volventi sferici.
La differenza sostanziale fra guide a manicotti e a pattini riguarda il tipo di carico che possono sopportate: le guide a manicotto possono lavorare solo con carichi radiali, mentre le guide a pattini possono essere sollecitate anche con momenti (figura 3).
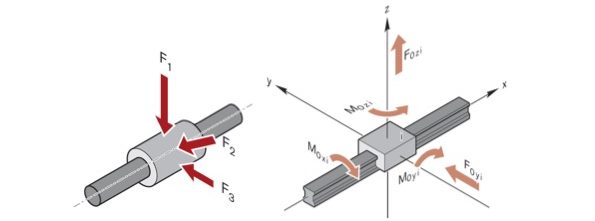
Questa differenza consente alle guide a pattini di poter essere impiegate anche teoricamente sono con un pattino (essendo impedito il ribaltamento), mentre nelle più comuni applicazioni vengono richiesti almeno due manicotti in modo da reagire ai carichi flettenti.
Cos’è una vite a ricircolo di sfere e come funziona?
Le viti a sfere sono elementi di trasmissione del moto che come noto sono in grado di trasformare un moto rotatorio in rettilineo (e in linea di massima anche viceversa). A differenza delle classiche viti di manovra, il contatto fra vite e madrevite non è strisciante, ma volvente il che consente di lavorare con un grande livello di precisione e sono adatte per applicazioni ad alte velocità (figura 4).

Esistono poi diverse tipologie di viti a ricircolo di sfere per soddisfare le diverse esigenze di movimentazione. Le singole caratteristiche dalla precisione richiesta, prestazione dinamiche, assenza di giochi, ecc.
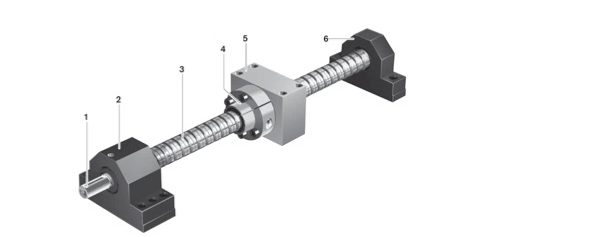
Quella che brevemente chiamiamo vite da ricircolo di sfere, è un’unità composta principalmente dai seguenti elementi (figura 5): la chiocciola con corpi volventi in ricircolo continuo, la viti, i cuscinetti d’estremità che consentono la rotazione e il fissaggio della vite, il codolo a cui viene connesso il motore.
La chiocciola e il suo supporto di collegamento alla tavola vengono movimentate dalla coppia torcente trasmessa dalla vite, a sua volta azionata da un motore. In alcune applicazioni viene invece posta in rotazione la chiocciola e quindi il moto lineare viene sviluppato dalla vite.
Come si calcolano le guide e le viti a ricircolo di sfere?
La progettazione delle guide lineari e delle viti a ricircolo di sfere può essere in linea di massima suddivisa in otto fasi:
- Definizione delle condizioni di funzionamento: tipologia del sistema di guida, disposizione dei supporti, ciclo dinamico e carichi di lavoro
- Calcolo delle sollecitazioni in funzione dei carichi agenti sui componenti.
- Calcolo del carico combinato equivalente sui singoli pattini
- Valutazione dell’eventuale del precarico
- Calcolo del carico dinamico equivalente sui componenti
- Calcolo della durata nominale o modificata a fatica
- Calcolo del carico statico equivalente sui componenti
- Calcolo coefficiente di sicurezza al carico statico
La procedura puntuale di progettazione con i relativi coefficienti e parametri da inserire viene sviluppata da ogni produttore, però in linea di massima il principio di calcolo si basa su quello sviluppato per i cuscinetti volventi e definito dalla norma DIN ISO 281, in cui viene calcolata la durata nominale a fatica che rappresenta la distanza che un componente è in grado di percorrere prima che si presentino i primi segni di fatica sulle superfici di rotolamento o sui corpi volventi (nelle guide lineari la durata a fatica è riferita alla distanza percorsa, mentre nelle unità viti a sfere è rappresentata dal numero di giri).
La teoria della durata è stata sviluppata da Lundberg e Palmgren che hanno messa a punto un modello in grado di prevedere la durata nominale a fatica attesa L di un componente volvente in funzione del carico.
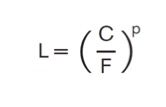
dove:
L è la durata nominale a fatica (distanza guide lineari o numero di giri nelle unità viti a sfere)
C è il fattore di carico dinamico
F è il carico equivalente applicato sul componente
p è l’esponente dell’equazione della durata a fatica in funzione del tipo di corpo volvente (p = 3 per guide lineari a sfere e per unità viti a sfere; p = 10/3 per guide lineari a rulli).
Come è noto la durata a fatica è un parametro altamente disperso, per cui occorre abbinarlo ad una probabilità di guasto, viene quindi definita la durata nominale a fatica (solitamente indicata come L10) che rappresenta la durata a fatica calcolata con una probabilità di durata pari al 90 %, ovvero che il 90 % di una quantità sufficientemente elevata dello stesso tipo di componenti è in grado di raggiungere o superare la durata a fatica calcolata prima che si manifestino segni di fatica.
Un aspetto molto importante nella progettazione delle guidi e viti a ricircolo di sfere è il calcolo dei carichi equivalenti.
Occorre innanzitutto considerare che durante il funzionamento agiscono di un sistema lineare agiranno carichi differenti e sarà quindi possibile definire i cicli di carico al cui il sistema è sottoposto.
Per semplificare il calcolo della durata a fatica si vengono definite delle metodologie per il calcolo di un carico equivalente opportunamente calcolato tenendo conto di tutti i carichi agenti sul componente.
Il carico equivalente è composto da due componenti che sono il carico statico equivalente e il carico dinamico equivalente.
Il carico statico equivalente viene calcolato per quei casi in cui il sistema è sottoposto a forze e momenti lungo diverse direzioni, in condizioni statiche.
Il carico dinamico equivalente viene invece calcolato quando il sistema è sollecitato a carichi variabili nel tempo.
Le formule per il calcolo dei carichi equivalenti dipendono dal tipo di sistema e quindi occorre seguire le indicazioni fornite da ogni costruttore.
A differenza delle guide, nelle viti il carico equivalente da considerare agirà solo in direzione assiale (tutti gli altri carichi vengono sostenuti dalle guide) e occorrerà anche eseguire una verifica sulla velocità di rotazione critica.
Andrea Mura, Dipartimento di Ingegneria Meccanica e Aerospaziale, Politecnico di Torino






